Концепції сучасного природознавства - Карпов Я. С. - 2.9.1 Принцип найменшої дії

У XVIII-XIX ст. багато фізиків і філософів вдавалися до серйозного аналізу й перегляду вчення Ньютона про простір і час. З того часу, як основи класичної механіки" набули завдяки Ньютонові своєї завершеної форми, їх значення продовжувало залишатися предметом суперечок — принаймні до 1905 р. Боротьба розгорталася на найрізноманітніших ділянках науки й життя. Теорія перевірялася в експедиціях, в астрономічних спостереженнях, в обчисленнях математиків, обговорювалася у філософських і наукових дискусіях, викладалася в підручниках і монографіях.

Там, де в Ньютона йшлося про абсолютний простір і час, де він посилався при цьому на експерименти, деякі з його послідовників заявляли, що вони не потребують таких гіпотез і навіть доходило до того, що вони зводили його другу аксіому до простого визначення; через це відмінність між математикою і фізикою як експериментальною наукою сильно зміщувалася за рахунок останньої, від якої було відділено так звану чисту механіку.

Інші, навпаки, наполягали на істотно експериментальному характері цієї аксіоми. Сторони, які брали участь у цих дуже заплутаних суперечках, намагалися навести численні аргументи на підтримку своїх точок зору.

"Начала" Ньютона були викладені важкою геометричною мовою. Доведення були громіздкі та складні. У XVIII ст. в механіку проникають методи диференціального й інтегрального числення, які не наважився застосувати у своїй основній праці один із творців цих методів.

У XVIII ст. відбувалися не тільки перетворення методів ньютонівської механіки. Це століття відзначене пошуками загальних принципів механіки, еквівалентних законам Ньютона, або навіть більш загальних, ніж ці принципи. У результаті цих пошуків було відкрито принципи можливих переміщень у статипі, принцип Даламбера й принцип найменшої дії Мопертюї-Ейлера в динаміці.

2.9.1 Принцип найменшої дії

Історія цього принципу корінням сягає Герона Александрійського, його твердження про найкоротший час поширення світла, за допомогою якого Герой обгрунтував закон відображення.

Ферма (1601-1665) застосував цей принцип до заломлення світла й сформулював закон заломлення світла, виходячи з постулату: "Природа діє найбільш легкими й доступними шляхами".

Пізніше цю ідею розвинув І. Бернуллі (1667-1748). Він зіставив принцип Ферма із запропонованою ним варіаційною механічною задачею про лінію найкоротшого спуску важкої точки в полі ваги (брахістохрону). Цю задачу Бернуллі сформулював у такий спосіб: "У вертикальній площині дано дві точки: А і В. Визначити траєкторію, рухаючись по якій під впливом власної ваги, тіло М, почавши рухатися з точки А, досягне іншої точки В у найкоротший час". У

принципі Ферма й у задачі про брахістохрону мова йде про встановлення мінімального значення інтеграла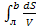

"Я, - писав І. Бернуллі, - відкрив дивну схожість між кривизною променя світла в середовищі, яке постійно змінюється, і нашою брахістохрониою кривою". Так уперше було помічено оптико-механічну аналогію, що відіграла важливу роль в історії фізики.

Надалі цю ідею розвивав стосовно Механіки П. Мюпертюї (1698-1759). У статті "Закон спокою" (1740) він поставив за мету вивести принцип рівноваги системи тіл і сформулював його як екстремальний принцип для деякої величини, яка дістала назву "суми сил спокою".

Через чотири роки потому Мопертюї виступив зі статтею "Узгодження різних законів природи", в якій стверджував, що закони оптики є наслідком "метафізичного закону", який полягає в тому, що "природа, реалізуючи свої дії, завжди вдається до найбільш простих засобів" і що принцип Ферма є принципом найменшої дії. Світло, на думку Мопертюї, вибирає шлях, "на якому кількість дії є найменшою". При цьому він пояснює, що слід розуміти під "кількістю дії". "Ця дія, — стверджує Мопертюї, — залежить від швидкості, з якою рухається тіло, і від простору, який долає останнє, але вона не є ні швидкістю, ні простором, узятими окремо. Кількість дії тим більша, чим більша швидкість тіла; вона пропорційна сумі добутків відрізків на швидкість, з якою тіло долає кожний з них". Принцип Ферма-Мопертюї виражається у вигляді твердження:

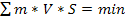
У сучасній редакції принцип Мопертюї стверджує: коли в природі відбувається якась зміна, кількість дії, необхідна для цієї зміни, є найменшою з можливих.