3.3.1 Робота в механіці, закон збереження та перетворення енергії в механіці
Серед законів збереження, перерахованих вище, найбільший інтерес становить той, який пов'язаний з енергією.
Ми знаємо, що споживання енергії постійно зростає, що нестача енергії впливає не тільки на повсякденне життя, але і на міжнародні відносини. Уявлення про енергію пов'язане в нашій свідомості з нафтою, вугіллям, падаючою водою, ураном. Енергія не тільки надає руху різним механізмам н обігріває будинки. Вона також необхідна для виробництва всіх предметів, якими ми користуємося і які нас оточують. Усі живі істоти в буквальному значенні поїдають енергію, щоб підтримувати життя.
Дати абсолютно точне, правильне й всеосяжне визначення енергії дуже складно. Адже енергія виявляється в безлічі різних форм. Автомобіль, що рухається, має енергію. Нерухома батарейка електронного годинника має енергію. Камінь на вершині скелі має енергію. Енергія міститься і в чайнику з окропом, і в шматочку вершкового масла, і в сонячному світлі.
Енергія є єдиним мірилом різних форм руху. Можливі два якісно різні способи передачі руху й відповідно передачі енергії від одного макроскопічного тіла до іншого — шляхом здійснення роботи й шляхом теплообміну.
Під процесом здійснення роботи розуміють такий процес взаємодії якого-небудь тіла з іншими тілами, у результаті якого змінюється механічний рух цього тіла або його положення відносно інших тіл. Такими, наприклад, є процеси зіткнення тіл, що рухаються, їхнє гальмування внаслідок явища тертя, а також будь-які процеси переміщення тіл під впливом сил взаємодії між ними.
Зміна енергії тіла в процесі здійснення роботи і називається роботою.
Розглянемо спочатку тільки ті форми енергії, що пов'язані з механічним рухом: кінетичну й потенційну.
Кінетична енергія — це енергія механічної системи, що залежить від швидкості руху її точок. Кінетична енергія матеріальної точки дорівнює половині добутку маси т цієї точки на квадрат її швидкості v, тобто
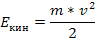
Кінетична енергія механічної системи дорівнює сумі кінетичних енергій усіх її точок.
Кінетична енергія зберігається тільки при зіткненнях (взаємодіях) певного типу, коли на тілах, що зіштовхуються, не залишається пошкоджень і вони не злипаються. Такі зіткнення називаються пружними. Тому єдиний спосіб довідатися, чи є зіткнення пружним, - переконатися, що сумарна кінетична енергія залишається незмінною.
Зміна кінетичної енергії системи при її переміщенні з положення і у положення 2 може відбуватися під дією прикладених до системи зовнішніх і внутрішніх сил. Ця зміна кінетичної енергії дорівнює сумі робіт Аі2 цих сил на даному переміщенні:
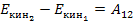
Фактично, останнє твердження є формулюванням теореми про зміну кінетичної енергії.
Усі сили, з якими має справу макроскопічна механіка, прийнято розділяти на консервативні й неконсервативні. Якщо сили взаємодії залежать тільки від конфігурації матеріальних точок системи (тобто від їхніх координат) і робота цих сил при переміщенні системи з довільного початкового положення в довільне кінцеве положення не залежить від шляху переміщення, а визначається тільки початковою і кінцевою конфігураціями системи, то такі системи називаються консервативними.
Можна довести, наприклад, що сила ваги F = m*g є консервативною. Консервативними є також сили гравітаційної взаємодії, електростатичної (кулонівської) взаємодії між зарядами.
Усі сили, що не є консервативними, називаються неконсервативними. До них належать, насамперед, так звані дисипативні сили, наприклад, сили тертя, що виникають при ковзанні якого-небудь тіла по поверхні іншого. Сюди ж належать сили опору, яких зазнає тіло, рухаючись у рідкому чи газоподібному середовищі. Усі ці сили залежать не тільки від конфігурації тіл, але і від їхніх відносних швидкостей. Вони спрямовані завжди проти швидкості тіла (щодо поверхні, по якій воно ковзає, чи щодо середовища, в якому воно рухається, зазнаючи опору). Тому якщо тіло ковзає по нерухомій поверхні або рухається в нерухомому середовищі, яке чинить опір, то при будь-якому русі тіла робота сил тертя, що діють на нього, є негативною. Таким чином, дисипативними називаються також сили, повна робота яких при будь-яких рухах у замкнутій системі завжди є негативною.
Необхідно відзначити ще один вид консервативних сил, які називаються гіроскопічними силами. Ці сили залежать від швидкості матеріальної точки й діють завжди перпендикулярно до цієї швидкості. Робота таких сил дорівнює нулю при будь-якому переміщенні матеріальної точки, зокрема при її русі по замкнутому шляху. Прикладом такої сили є сила Лоренца, тобто сила, що діє на заряджену частинку в магнітному полі.
Робота сили, прикладеної до тіла, визначається як
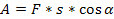
де F — величина діючої сили;
s — модуль переміщення тіла;
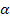 — кут між напрямком дії сили й напрямком переміщення. Якщо на систему діють тільки консервативні й гіроскопічні сили, то для неї можна ввести поняття потенційної енергії.
— кут між напрямком дії сили й напрямком переміщення. Якщо на систему діють тільки консервативні й гіроскопічні сили, то для неї можна ввести поняття потенційної енергії.
Яке-небудь довільне положення системи, що характеризується заданням координат її матеріальних точок, умовно приймемо за нульове. Робота, яку здійснюють консервативні сили при переході системи з розглянутого положення в нульове, називається потенційною енергією системи. Робота консервативних сил не залежить від шляху переміщення, а тому потенційна енергія системи при фіксованому нульовому положенні залежить тільки від координат матеріальних точок у розглянутому положенні. Іншими словами, потенційна енергія системи U є функцією тільки її координат.
Значення потенційної енергії залежить від того, яке положення системи умовно прийняти за нульове. Якщо за нульове прийняти положення 0 (див. мал.),
1
 |
то в положенні 1 система матиме потенційну енергію U =
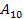 , що дорівнює роботі консервативних сил при переході системи з положення 1 в положения 0. Якщо ж за нульове прийняти положення 0', то потенційна енергія дорівнюватиме U' =
, що дорівнює роботі консервативних сил при переході системи з положення 1 в положения 0. Якщо ж за нульове прийняти положення 0', то потенційна енергія дорівнюватиме U' = 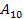 . Унаслідок консервативності сил, що діють у системі, робота уздовж шляху 10' дорівнює роботі уздовж шляху 100':
. Унаслідок консервативності сил, що діють у системі, робота уздовж шляху 10' дорівнює роботі уздовж шляху 100':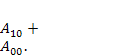 або
або
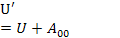
Робота у4м. постійна, тобто не залежить від координат системи в розглянутому положенні 1. Вона цілком визначається вибором нульових положень 0 і 0'. Зрозуміло, що при заміні одного нульового положення на інше потенційна енергія системи змінюється на постійну величину. Таким чином, потенційна енергія системи визначена не однозначно, а з точністю до довільної сталої.
Нехай система перейшла з положення 1 в положення 2 по якому-небудь шляху 12 (див. мал.).

Роботу 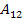 , виконану консервативними силами при такому переході, можна виразити через потенційні енергії
, виконану консервативними силами при такому переході, можна виразити через потенційні енергії 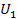 й
й 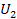 у станах 1 і 2. Для цього уявимо, що перехід здійснено через нульове положення 0, тобто по шляху 102. Так як сили консервативні, то
у станах 1 і 2. Для цього уявимо, що перехід здійснено через нульове положення 0, тобто по шляху 102. Так як сили консервативні, то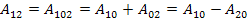 . За визначенням потенційної енергії
. За визначенням потенційної енергії 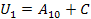 ,
, 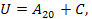 де С — та сама стала. Таким чином,
де С — та сама стала. Таким чином,
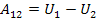
тобто робота консервативних сил дорівнює величині зменшення потенційної енергії системи.
Робота 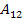 , як було показано вище, може бути також виражена через збільшення кінетичної енергії.
, як було показано вище, може бути також виражена через збільшення кінетичної енергії.
Тоді 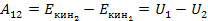 ,
,
звідки 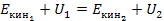 .
.
Сума кінетичної і потенційної енергій системи називається її повною енергією Е. Таким чином,
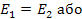
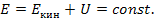
У системі з одними тільки консервативними (і гіроскопічними) силами повна механічна енергія залишається незмінною. Можуть відбуватися лише перетворення потенційної енергії на кінетичну й навпаки, але повний запас енергії системи змінитися не може. Це положення називається законом збереження енергії в механіці.
3.4 Другий закон термодинаміки та принцип зростання ентропії
3.4.1 Другий закон термодинаміки
3.4.2 Ідеальний цикл Карно
3.4.3 Поняття ентропії
3.4.4 Ентропія та імовірність
3.4.5 Порядок і хаос. Стріла часу
3.4.6 Проблема теплової смерті всесвіту. Флуктаційна гіпотеза Больцмана
3.4.7 Синергетика. Народження порядку з хаосу
3.5 Квантова механіка