Концепції сучасного природознавства - Карпов Я. С. - 3.4.3 Поняття ентропії

Для ідеальної машини Карно справджується вираз

Звідси випливає рівність

Так як кількість теплоти передається холодильнику, її треба взяти зі знаком "мінус". Отже, одержуємо вираз:

Будемо писати AQ замість Q, підкреслюючи, що йдеться про порцію AQ,, яку робоче тіло отримало від нагрівача, і порцію яку воно втратило в холодильнику:

Цей вираз схожий на закон збереження, а це, у свою чергу, не може не привернути уваги до величини

У 1865 році Клаузіус увів нове поняття "ентропія" (entropia — від грецького слова "поворот", "перетворення"). Клаузіус обчислив, що існує деяка величина S, яка подібно до енергії, тиску, температури характеризує стан газу. Коли газ отримує деяку кількість теплоти A Q то ентропія S зростає на величину, що дорівнює

У попередньому розділі зазначалося, що протягом тривалого часу вчені не розмежовували такі поняття, як температура й теплота. Однак ряд явищ указував на те, що ці поняття таки варто розрізняти. Так, при таненні льоду теплота витрачається, а температура льоду в процесі плавлення не змінюється. Після того, як Клаузіус увів поняття ентропії, стало зрозуміло, де проходить межа між поняттями теплоти й температури. Справа в тому, що не можна говорити про якусь кількість теплоти, що міститься в тілі. Це поняття не має смислу. Теплота може передаватися від тіла до тіла, перетворюватися на роботу, виникати при терті, але при цьому вона не є величиною, що зберігається. Тому теплота визначається у фізиці не як вид енергії, а як міра зміни енергії. У той же час ентропія, яку запропонував Клаузіус, виявилася величиною, що зберігається в оборотних процесах. Це означає, що ентропія системи може розглядатися як функція стану системи, тому що її зміна не залежить від виду процесу, а залежить тільки від початкового й кінцевого станів системи. Доведемо, що в ідеальному циклі Карно ентропія зберігається.

Розглянемо величину 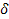Q, яка позначає нескінченно мале збільшення теплоти — настільки мале, що система зберігає одне й те саме значення температури, незмінне

у всьому об'ємі розглянутої системи. Тобто припустимо, що система в усі моменти часу перебуває у стані теплової і механічної рівноваги, і будь-яка зміна її стану складається з послідовності рівноважних станів, кожен з яких лише нескінченно мало відрізняється від попереднього. Саме такий характер поведінки системи реалізується в оборотних процесах.

Якщо процес оборотний, як у циклічному циклі Карно, то

Із цього співвідношення випливає, щоентропія робочого тіла на першій стадії зростає рівно настільки, наскільки вона зменшується на третій стадії. На другій і на четвертій стадіях ентропія робочого тіла не змінюється, тому що процеси тут протікають адіабатично, без теплообміну.

Іншими словами, у випадку оборотних процесів 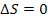, тобто S = const — ентропія ізольованої системи у випадку оборотних процесів стала.

При необоротних процесах одержуємо закон зростання ентропії:

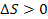
Для того, щоб здійснити оборотний процес, необхідно домогтися дуже повільного розширення або стиснення робочого тіла, щоб зміни системи являли собою послідовність рівноважних станів. У такому циклі виконання якої-небудь корисної роботи вимагає нескінченно великої кількості часу. Щоб одержати роботу протягом коротких проміжків часу, тобто достатню потужність, доводиться порушувати умови ідеального циклу. А це відразу призводить до різниці температур на різних ділянках системи, до потоків тепла від більш гарячих ділянок до менш гарячих, тобто до зростання ентропії системи.

Щоб описати термодинамічні процеси, першого закону термодинаміки виявляється недостатньо, тому що перший закон термодинаміки не дозволяє визначити напрямок протікання процесів у природі. Той факт, шо ентропія ізольованої системи не може убувати, а тільки зростає і досягає максимального значення в рівноважному стані, є відображенням того, що в природі можливі процеси, що протікають тільки в одному напрямку — у напрямку передачі тепла від більш гарячих тіл до менш гарячих.

Таким чином, сформулюємо ще раз деякі положення другого закону термодинаміки. Усі вони є еквівалентними.

1. Процеси, в яких єдиним кінцевим результатом є перехід тепла від тіла, менш нагрітого, до тіла, більш нагрітого, відбуватися не можуть.

У природі всі процеси протікають тільки в одному напрямку — у напрямку передавання тепла від більш гарячих тіл до менш гарячих.

2. ККД будь-якої теплової машини завжди менший, ніж 100 %, тобто неможливий вічний двигун (перпетуум-мобіле) другого роду (тому що неможливо побудувати теплову машину, що працює не за рахунок перепаду теплоти, а за рахунок теплоти одного нагрівача).

ККД будь-якої реальної теплової машини завжди менший від ККД ідеальної теплової машини.

3. Ентропія ізольованої системи при протіканні необоротних процесів зростає, тому що система, не зазнаючи ніяких зовнішніх впливів, переходить з менш імовірного стану в більш імовірний (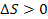). Ентропія системи, що перебуває в рівноважному стані, максимальна й постійна. ().

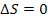Це останнє формулювання слід обговорити більш докладно.