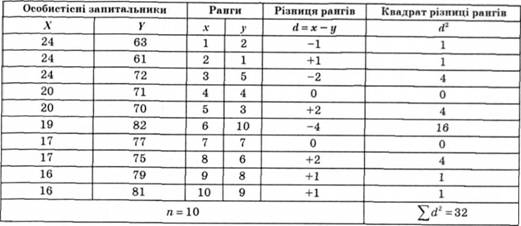
Рангова кореляція Спірмена (кореляція рангів). Рангова кореляція Спірмена — найпростіший спосіб визначення міри зв'язку між факторами. Назва методу свідчить про те, що зв'язок визначають між рангами, тобто рядами одержаних кількісних значень, ранжованих у порядку зниження або зростання. Треба мати на увазі, що, по-перше, рангову кореляцію не рекомендовано проводити, якщо зв'язок пар менший чотирьох і більший двадцяти; по-друге, рангова кореляція дає змогу визначати зв'язок і в іншому випадку, якщо значення мають напівкількісний характер, тобто не мають числового виразу, відображають чіткий порядок прямування цих величин; по-третє, рангову кореляцію доцільно застосовувати в тих випадках, коли достатньо одержати приблизні дані. Приклад розрахунку коефіцієнта рангової кореляції для визначення питання: чи заміряють запитальник X і У подібні особистісні якості досліджуваних. За допомогою двох запитальників (X і У), які вимагають альтернативних відповідей "так" або "ні", отримали первинні результати — відповіді 15 досліджуваних (N = 10). Результати подали у вигляді суми стверджувальних відповідей окремо для запитальника X і для запитальника У. Ці результати зведено в табл. 5.19.
Таблиця 5.19. Табулювання первинних результатів для розрахунку коефіцієнта рангової кореляції за Спірменом (р)*

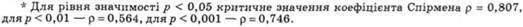
Аналіз зведеної кореляційної матриці. Метод кореляційних плеяд.
Приклад. У табл. 6.18 наведено інтерпретації одинадцяти змінних, які тестують за методикою Векслера. Дані одержали на однорідній вибірці у віці від 18 до 25 років (n = 800).
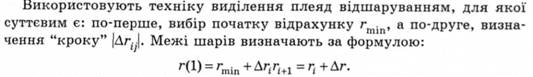
Перед розшаровуванням кореляційну матрицю доцільно ранжувати. Для цього у вихідній матриці обчислюють середні значення коефіцієнтів кореляції кожної змінної зі всіма решта.
Потім за табл. 5.20 [24, с. 20] визначають припустимі рівні розшарування кореляційної матриці при заданих довірчій імовірності 0,95 і n — кількості
Таблиця 6.20. Висхідна кореляційна матриця
| Змінні | 1 | 2 | 3 | 4 | б | 0 | 7 | 8 | 0 | 10 | 11 | M(rij) | Ранг |
| 1 | 1 | 0,637 | 0,488 | 0,623 | 0,282 | 0,647 | 0,371 | 0,485 | 0,371 | 0,365 | 0,336 | 0,454 | 1 |
| 2 | 1 | 0,810 | 0,557 | 0,291 | 0,508 | 0,173 | 0,486 | 0,371 | 0,273 | 0,273 | 0,363 | 4 | |
| 3 | 1 | 0,346 | 0,291 | 0,406 | 0,360 | 0,818 | 0,346 | 0,291 | 0,282 | 0,336 | 7 | ||
| 4 | 1 | 0,273 | 0,572 | 0,318 | 0,442 | 0,310 | 0,318 | 0,291 | 0,414 | 3 | |||
| 5 | 1 | 0,354 | 0,254 | 0,216 | 0,236 | 0,207 | 0,149 | 0,264 | 11 | ||||
| 6 | 1 | 0,365 | 0,405 | 0,336 | 0,345 | 0,282 | 0,430 | 2 | |||||
| 7 | 1 | 0,310 | 0,388 | 0,264 | 0,266 | 0,310 | 9 | ||||||
| 8 | 1 | 0,897 | 0,363 | 0,388 | 0,363 | 5 | |||||||
| 9 | 1 | 0,388 | 0,430 | 0,846 | 6 | ||||||||
| 10 | 1 | 0,336 | 0,310 | 8 | |||||||||
| 11 | 1 | 0,300 | 10 |
Позначення: 1 — загальна обізнаність; 2 — понятійність; 3 — уважність; 4 — вдатність ДО узагальнення; б — безпосереднє запам'ятовування (на цифрах); 6 — рівень опанування рідною мовою; 7 — швидкість оволодіння сенсомоторними навичками (кодування символами); 8 — спостережливість; 9 — комбінаторні здібності (до аналізу й синтезу); 10 — здібність до організації частин в осмислене ціле; 11 — здібність до евристичного синтезу; M(rij)— середнє значення коефіцієнтів кореляції змінної з рештою змінних спостережень (у нашому випадку n = 800): r(0) — значення нульової "розсікаючої” площини — мінімальна значима абсолютна величина коефіцієнта кореляції (n - 120, r(0) = 0,236; n = 40, r(0) = 0,407); |∆r| — допустимий крок розшарування (n = 40, |∆r| = 0,558); в — допустима кількість рівнів розшарування (n = 40, s = 1; n = 120, s = 2); r(1), r(2),... , r(9) — абсолютне значення січної площини (n = 40, r(1) = 0,965).
Для n = 800 знаходимо значення гтіп і меж гі після чого розшаровуємо ранжировану кореляційну матрицю, виділяючи кореляційні плеяди всередині шарів, або відокремлюємо частини кореляційної матриці, вимальовуючи об'єднання кореляційних плеяд для вище розташованих шарів (рис. 5.5).
Змістовний аналіз одержаних плеяд виходить за межі математичної статистики. Треба зазначити два формальні показники, які допомагають при змістовній інтерпретації плеяд. Одним суттєвим показником слугує степінь вершини, тобто кількість ребер, які примикають до вершини. Змінна з найбільшою кількістю ребер є "ядром" плеяди і її можна розглядати як індикатор решти змінних цієї плеяди. Другий суттєвий показник — щільність зв'язку. Змінна може мати менше зв'язків в одній плеяді, але тісніші, і більше зв'язків в іншій плеяді, проте менш тісних.
Передбачення і оцінювання. Рівняння у = b1x + b0 називається загальним рівнянням прямої. Воно свідчить про те, що пари точок (x, у), які
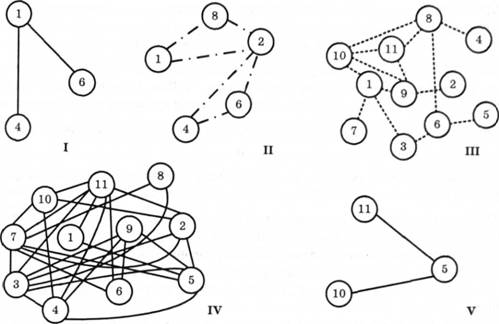
Рис. 5.5. Кореляційні плеяди, отримані розшаруванням матриці
лежать на деякій прямій, пов'язані так, що для будь-якого значення х величину у у що перебуває з ним у парі, можна знайти, помноживши х на деяке число b1 додавши друге, число b0 до цього добутку.
Коефіцієнт регресії дає змогу визначити міру зміни наслідкового фактора при зміні причинного фактора на одну одиницю. Абсолютні величини характеризують залежність між перемінними факторами за їхніми абсолютними значеннями. Коефіцієнт регресії обчислюють за формулою:
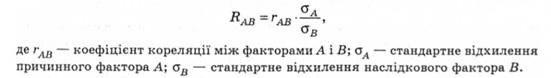
Планування й аналіз експериментів. Планування й аналіз експериментів — це третя важлива галузь статистичних методів, які розроблені для знаходження і перевірки причинних зв'язків між змінними.
Для дослідження багатофакторних залежностей останнім часом все частіше використовують методи математичного планування експерименту.
Можливість одночасного варіювання усіма факторами дає змогу: а) зменшити кількість дослідів;
б) звести помилку експерименту до мінімуму;
в) спростити обробку одержаних даних;
г) забезпечити наочність і легкість у порівнянні результатів.
Кожний фактор може набувати деяку відповідну кількість різних значень, які називаються рівнями і позначають —1, 0 та +1. Фіксований набір рівнів факторів визначає умови одного з можливих дослідів.
Сукупність усіх можливих поєднань обчислюють за формулою:
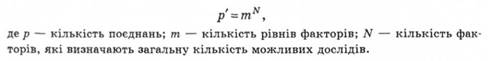
Повним факторним експериментом називається експеримент, в якому реалізуються всі можливі поєднання рівнів факторів. Повні факторні експерименти можуть володіти властивістю ортогональності. При ортогональному плануванні фактори в експерименті є некорельованими, коефіцієнти регресії, які вираховують у підсумку, визначають незалежно один від одного.
Важливою перевагою методу математичного планування експерименту є його універсальність, придатність у багатьох галузях досліджень.
Розглянемо приклад порівняння впливу деяких факторів на формування рівня психічної напруги у регулювальників кольорових телевізорів.
В основу експерименту покладено ортогональний план 23 (три фактори змінюються на двох рівнях).
Експеримент проводили за повним планом 23 з трикратним повторенням.
Ортогональне планування базується на побудові рівняння регресії. Для трьох факторів воно виглядає так:

Опрацювання результатів у цьому прикладі охоплює:
а) побудову ортогонального плану 23 з таблицею для розрахунку;
б) обчислення коефіцієнтів регресії;
в) перевірку їх значимості;
г) інтерпретацію одержаних даних.
Для коефіцієнтів регресії згаданого рівняння треба було поставити N= 23 = 8 варіантів, щоб мати змогу оцінити значущість коефіцієнтів, де кількість повторень К дорівнювало 3.
Складена матриця планування експерименту мала такий вигляд.
Визначення цільових ознак.
Визначення прогностичних ознак.
Виявлення функції зв'язку.
Інтерпретація й аналіз даних.
Форма подання результатів дослідження, завершення.
Універсальні психодіагностичні методики.
Оцінка психічного розвитку.
Розділ 6. ПСИХОЛОГІЧНЕ ВИВЧЕННЯ ПРОФЕСІЙ
6.1. Професіографія та її цілі