Банківські операції - Прасолова С.П. - 1.5. Розрахунки з урахуванням інфляції

При нарахуванні складних процентів (процентів, що капіталізуються) сума процентів, нарахованих після першого періоду нарахування, що є частиною загального терміну зберігання вкладу, не виплачується, а додається до базової суми вкладу. За другий період нарахування проценти будуть нараховуватись виходячи з суми базового вкладу, збільшеного на суму процентів, нарахованих за перший період і так далі за кожний наступний період нарахування. Тобто, на відміну від простих процентів, база для нарахування складних процентів буде збільшуватися з кожним періодом нарахування, що є частиною загального терміну зберігання вкладу, а загальна сума вкладу з нарахованими процентами зі врахуванням раніше прийнятих умовних позначень буде визначатися за формулою:

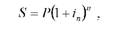
де: іп - номінальна ставка складних процентів; п - термін вкладу в роках.

Сума нарахованих процентів буде дорівнювати:

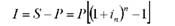
Складні проценти можуть нараховуватись також декілька раз на рік (наприклад, за місяцями, кварталами, півріччям). Сума вкладу з процентами (нарощена сума) при терміну вкладу п років буде дорівнювати:

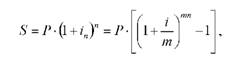
де: т - кількість періодів нарахування в одному році, яка за щомісячного нарахування капіталізованих відсотків буде дорівнювати 12;

і - номінальна річна ставка процентів;і

іп - ставка процентів за період нарахування, яка дорівнює - .т

Сума нарахованих процентів, відповідно, складе:

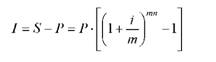
Приклад 9.

Банк нараховує складні проценти за номінальною ставкою 16 % річних. Визначити діючу ставку складних процентів, якщо складні проценти нараховуються щомісячно, щоквартально і за півріччя.

Розв'язок:

Для рішення задачі використовується елемент формули (1.11.): а) при щомісячному нарахуванні процентів, діюча ставка процентів за період нарахування складе:

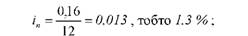
б) при щоквартальному нарахуванні процентів:

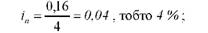
в) при нарахуванні за півріччями:

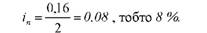
Приклад 10.

Депозит в розмірі 5000 грн. покладено в банк на 3 роки. Визначити суму нарахованих процентів за цей термін, якщо річна ставка складних процентів складає 10 %.

Розв'язок:

Для рішення задачі використовується формула (1.10.): І = 5000 [(1 + 0,1)3 -1] = 1655 грн.

Приклад 11.

Складні проценти на вклади нараховуються щоквартально за номінальною річною ставкою 10 % річних. Визначити суму процентів, нарахованих на вклад 2000 грн.:

а) за півроку;

б) за два роки.

Розв'язок:

Для рішення задачі використовується формула (1.12.): а) сума процентів, нарахованих за півріччя складе:

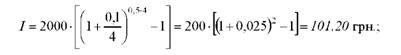
б) сума процентів, нарахованих за 2 роки складе:

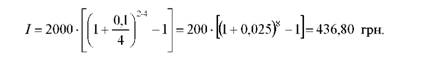
1.5. Розрахунки з урахуванням інфляції

При визначенні суми нарахованих процентів за вкладами необхідно враховувати рівень інфляції, оскільки якщо зростання інфляції перевищує суму зростання доходів вкладників, то це призводить до знецінення їх доходів.

Реальне значення суми вкладу разом з нарахованими процентами з урахуванням інфляції Бр можна визначити за формулою (1.13.):

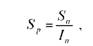
де Бп - номінальна сума вкладу з нарахованими процентами; Іп - індекс інфляції, який може бути визначено за формулою

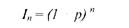
де р - рівень інфляції;

п - кількість періодів, за які враховуються рівні інфляції

Приклад 12.

Вклад у сумі 5000 грн. покладено в банк на півроку з щомісячним нарахуванням складних процентів за номінальною ставкою 16 % річних. Визначити реальний доход вкладника, якщо рівень інфляції складав 2 % на місяць.

Розв'язок:

Номінальну суму вкладу з процентами визначаємо за формулою

(1.11):

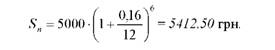
Індекс інфляції, розрахований за формулою (1.14) за півроку складе:

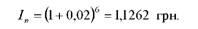
Відповідно, сума вкладу з процентами з точки зору її купівельної спроможності, визначена за формулою (1.13) буде дорівнювати:

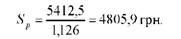
Таким чином, реальний доход (збиток) вкладника складе: Д (З) = 4805,98 - 5000 = - 1940,2 грн., що означає реальне знецінення доходу вкладника.