Математична статистика - Руденко В.М. - Міри мінливості (ММ)

Обмеженість мір центральної тенденції для характеристики сукупностей можна продемонструвати на прикладі двох вибірок (рис. 2.29), які мають різні розподіли, проте однакові (і це не складно перевірити) МЦТ (значення моди Мо, медіани Ми і середнього X дорівнюють 4).

Рис. 2.29. Властивості ММ

Проте вибірки мають істотну різницю значень основних ММ: дисперсій * _х і стандартних відхилень 8_х (див. два останні стовпчики рис. 2.29). Можна відзначити своєрідну "чутливість" показників ММ щодо властивостей сукупності.

Дисперсія вибірки обсягом п визначається як:

2 (х -X)² + (х2 -X)² + ... + (хп -X)²

^ =-:-^{, (2.3)}

п-1

_аб0 *² = ^* ~> , д_Є X - середнє арифметичне вибірки. п -1

Дисперсія вибірки *²_х, що розрахована за цією формулою, є незміщеною оцінкою свого генерального параметра а²_х завдяки внесенню поправки Бесселя п/(п-1), тобто:

*2 ^(хі ~^X)2 Л^(хі ~^X)2 . (2.4)

п п - 1 п - 1

Різницю п-1 називають числом степенів вільності к - кількість об'єктів або значень у складі обмеженої статистичної сукупності, які можуть вільно варіювати. Якщо обмежень вільності варіації існує декілька (у), то число степенів вільності дорівнюватиме к= п-у (де у - грецька літера "ню").

Чисельник формули дисперсії можна перетворити у такий спосіб:

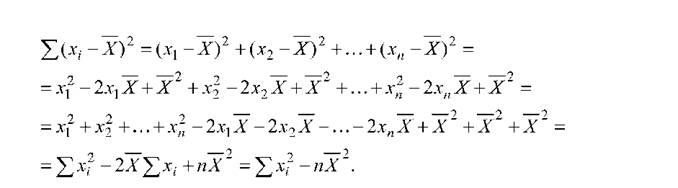
Тоді формула дисперсії має такий вигляд:

*² = -^(2х² "пХ²). (2.5)

п-1

Якщо дані представлено розподілами частот, дисперсія визначається як

*² = -Е /і (х - X)², (2.6)

п -1

де Хі - варіанти незгрупованих частот або центральні значення класових інтервалів у разі згрупованих частот;/ - диференціальні частоти, X - середнє.

Дисперсія служить мірою однорідності сукупностей емпіричних даних. Чим вища однорідність, тим нижче значення дисперсії. Для повністю однорідних сукупностей дисперсія дорівнює нулю.

Дисперсія генеральної сукупності обсягом N визначається як:

або = ^ ^(Хі-, де р = N ^ х_і - середнє арифметичне генеральної сукупності.

Стандартне відхилення вибірки визначається як у_х = д/УХ~. (2.8) Стандартне відхилення генеральної сукупності а_х = ^оХ". (2.9)

Коефіцієнт варіації У_х використовується у разі порівняльної оцінки різноякісних середніх величин і визначається (у тому числі у %) як відношення стандартного відхилення до середнього арифметичного:

у_і = у_х /X -100% . (2.10)

Асиметрія А_х характеризує ступінь несиметричності розподілу відносно його середнього. Позитивна асиметрія вказує на відхилення вершини розподілу в бік від'ємних значень, негативна - у бік додатних.

Ax = -ц--i(x -X)³. (2.11)

Ексцес E_x характеризує відносну опуклість або згладженість розподілу вибірки порівняно з нормальним розподілом. Позитивний ексцес позначає відносно загострений розподіл, негативний - відносно згладжений.

Ex =-^L-₄o£(X -X)⁴ -3. (2.12)

^П ■ ⁽Sx ⁾ i=1

"Стандартом" розподілів служить нормальний розподіл N(ji,o) з нульовою асиметрією і ексцесом. Для нього А_х = 0 - нормальний розподіл є симетричним відносно середнього значення, і Е_х = 0 - розподіл є "ідеальний" - не загострений і не згладжений.

Зауваження. Для визначення вибіркових значень асиметрії A_x та ексцесу E_x застосовують точні розрахункові формули, аналогічні тим, що використовує MS Excel:

Для асиметрії

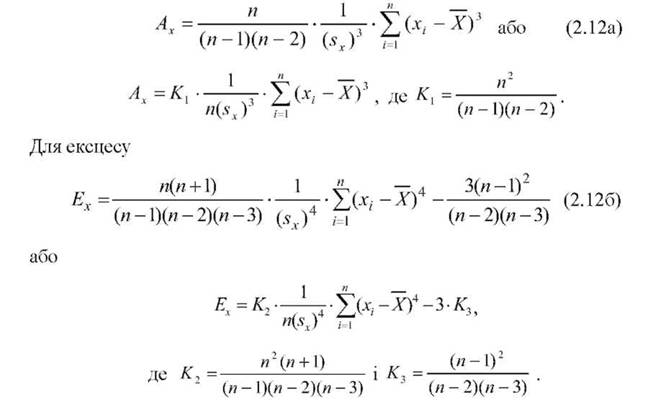
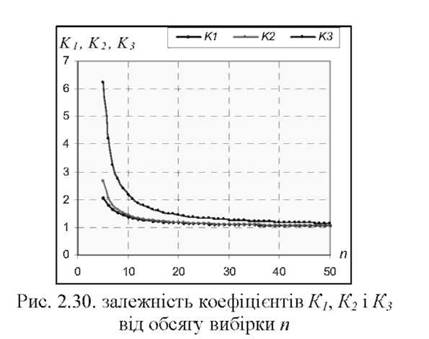
На рис. 2.30 показано, що коефіцієнти К], К₂ і К₃ при збільшені обсягу вибірки п асимптотично наближаються до одиниці (приблизно для п>30), а формули (2.12а) і (2.126) переходять у формули (2.11) і (2.12) відповідно.

Пропонуємо самостійно визначити, наскільки можуть різнитися результати точних і "спрощених" розрахунків ММ залежно від обсягу вибірки п.

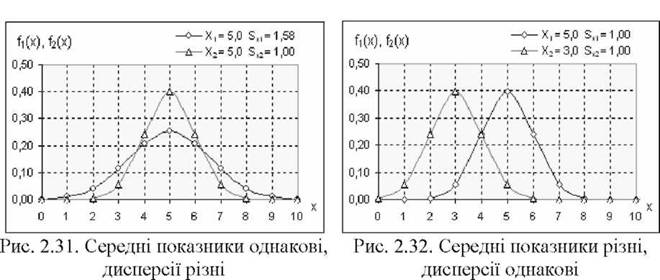
На якісному рівні можна наочно оцінити показники описової статистики завдяки вибірковим розподілам частот. Наприклад, форма розподілів на рис. 2.31 свідчить про однакові показники МЦТ (середні, моди і медіани вибірок однакові) і різні показники ММ (дисперсії і стандартні відхилення різні).

На рис. 2.32 показано розподіли двох однакових за однорідністю вибірок (дисперсії однакові), проте різних за середніми показниками. Ці вибірки мають також нульові значення асиметрії і ексцесу.

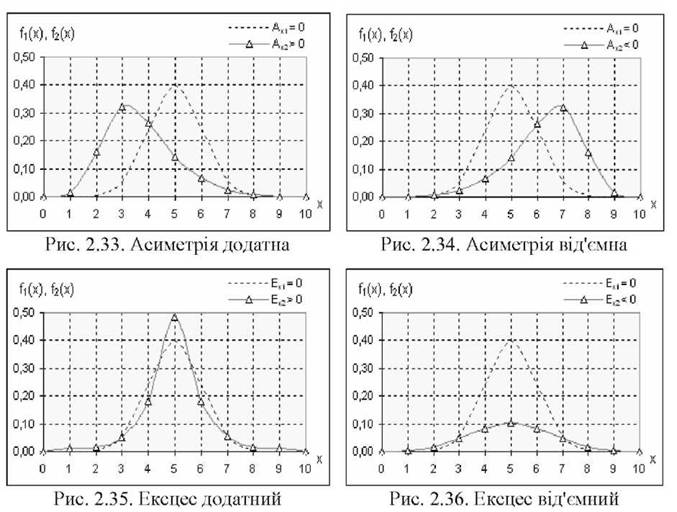
На рис. 2.33 - 2.36 продемонстровано, як форма розподілу частот може бути "деформована" відносно форми нормального (стандартного) розподілу. Саме показники асиметрії та ексцесу використовуються для перевірки відповідності емпіричного розподілу нормальному законові (див. розділ 5.2)