Математична статистика - Руденко В.М. - Повторні випробування

Повторні випробування

Явища і процеси, що вивчає психологія, - це, як правило, складні події. Тому формування теоретичної бази опису таких подій зручно розглядати на прикладі повторних випробувань. Тестування та іспити студентів можна вважати при деяких умовах прикладом таких випробувань.

З класичного визначення ймовірність - це число, до якого наближається частота появлень бажаної події при збільшенні незалежно виконаних випробовувань. До того ж і ймовірність, і частота виражаються в долях одини-

¹⁶ {Іноді пишуть "закони великих чисел", маючи на увазі основні теореми (Бе-рнуллі, Чебишева, центральної граничної теореми та ін.).}

7. Охарактеризуйте розподіл, функція якого її(х < 100) =| /(х)сіх = 0,50.

8. Яка інтерпретація площі під графіком щільність розподілу змінної?

9. Яка ймовірність визначається розподілом і щільністю розподілу?

10. Як визначити ймовірність за процентилем нормального розподілу?

11. Що таке математичне сподівання випадкової величини?

12. Поясніть властивості математичного сподівання випадкової величини.

13. Сформулюйте означення моди і медіани випадкової величини.

14. Сформулюйте означення дисперсії випадкової величини.

15. Охарактеризуйте властивості дисперсії випадкової величини.

16. Які показники називають початковим і центральним моментом к-то порядку випадкової величини?

17. Чим відрізняються формули початкового і центрального моментів випадкової величини?

18. Повторіть математичні процедури завдань за прикладами 3.11 - 3.15.

ці, їхні чисельні значення розміщені між нулем і одиницею, хоча, як відомо, частота випадкової величини і її ймовірність не співпадають в ідеалі.

Ймовірність, яку можна вказати до випробувань, називають апріорною. Наприклад, при підкиданні монети наперед відомо, що вона може впасти вгору "гербом" або "цифрою". Тут можливі лише дві події, ймовірності яких (якщо монета ідеальна) однакові: /"("герб") = /"("цифра") = 54 = 0,5.

Інша ситуація може мати місце при випробовуваннях, наприклад, впливу нових педагогічних технологій або психологічних методик на окремих осіб (школярів, студентів тощо) або на весь колектив. Результати таких випробувань передбачити наперед неможливо. Статистична ймовірність здійснення таких подій може бути встановлена тільки на підставі досліду, тобто апостеріорі.

Для практики застосування математичного апарату теорії ймовірностей важливе значення має відповідь на питання про те, чи співпадають апріорні (теоретичні) ймовірності зі статистичними (емпіричними) ймовірностями, представленими у вигляді частот? І якщо так, то при яких умовах?

Даючи принципово позитивну відповідь на це питання, численні досліди і

т

спостереження показали, що частоти випадкових подій типу - наближа-

п

ються до їхніх ймовірностей р у міру збільшення числа випробувань и. Наприклад, якщо одну й ту ж монету підкидати велику кількість разів, то в якомусь числі випробувань випаде "герб", а в інших випаде "цифра". Примітно те, що чим більше здійснено випробувань, тим емпірична частота події стає ближчою до її теоретичної ймовірності (для ідеальної монети/>=0,5).

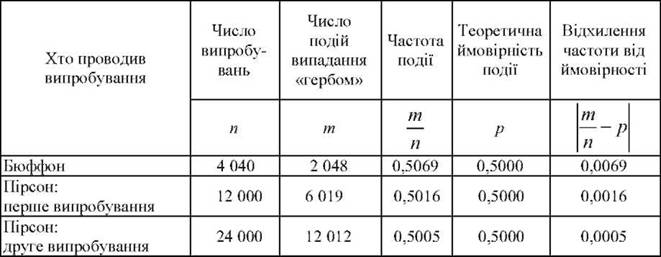
Існують і прямі експериментальні підтвердження того, що частота здійснення деяких подій близька до ймовірності, визначеної з теоретичних міркувань, наприклад, результати випробувань з підкиданням монети (табл. 3.6).

З табл. 3.6 видно, що при збільшені числа випробувань п відхилення час_т

тоти події від її ймовірності--р зменшується. У цьому факті є прояв дії

п

так званого закону великих чисел: вибіркові характеристики при зростанні числа дослідів наближаються до теоретичних, а це дає можливість оцінювати параметри імовірнісних моделей за даним дослідів.

Таблиця 3.6

Результати випробувань

Закон великих чисел носить об'єктивний характер і має відповідну емпіричну базу. Висновки закону підтверджують, наприклад, досліди Кетле: в урну поміщали 20 білих і 20 чорних куль, потім витягували з неї навмання одну кулю, реєстрували її колір і повертали кулю назад. Кожне випробування повторювали багато разів. Ймовірність появи білої або чорної кулі залишалася при цьому постійною, рівною 1/2 (див. табл. 3.7).

Таблиця 3.7

Результати дослідів Кетле

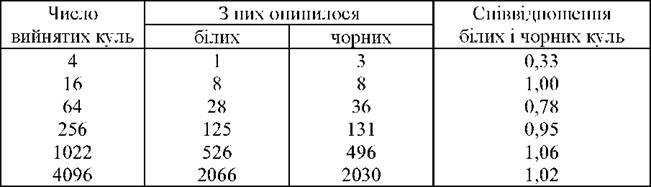
З табл. 3.7 видно, як із збільшенням числа випробувань співвідношення білих і чорних куль наближається до одиниці.

т

Закон великих чисел стверджує, що частота - події А буде скільки зап

вгодно близькою до її ймовірності р, якщо число випробувань п необмежено зростає. Можна взяти скільки завгодно мале число є і порівнювати його з різницею між відносною частотою і ймовірністю події. Ймовірність того, що ця різниця перевищить число є, прагнутиме до нуля при прагненні числа випробувань п до нескінченності:

Отже, частота події і її імовірність не співпадають, проте різниця між ними зменшується при збільшенні числа випробувань. Це значить, що статистичні закономірності виявляються тільки у багаторазових повторних випробуваннях і кількість таких випробувань п повинна бути значною.