Математична статистика - Руденко В.М. - Теорема Чебишева

Теорема Бернуллі стверджує: якщо т - кількість подій А в п попарно незалежних випробуваннях, а р є ймовірність настання події А в кожнім з випробувань, то при будь-якому є>0 справедлива нерівність

Ця формула є першим в історії варіантом закону великих чисел і по суті вважається початком теорії ймовірностей як галузі математичної науки. Відтоді теорії вибіркового методу стають основою математичної статистики.

Теорема Бернуллі дає можливість оцінити кількості незалежних випробувань п при певних умовах їх проведення.

Приклад 3.16. Ймовірність того, що навмання вибраний студент складе залік, дорівнює 90%. Скільки треба перевірити студентів, щоб з імовірністю 80% виявити успішно підготовлених студентів. Похибка при цьому не повинна перевищувати 10%.

Рішення:

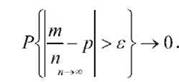
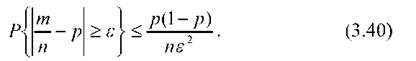
Визначимо відповідні до теореми Бернуллі позначення:

р = 0,90 - ймовірність того, що навмання вибраний студент складе залік;

є = 0,10 - похибка процедури перевірки студентів;

рі OL - p > o_,101 =0,80 - ймовірність виявлення підготовлених студентів.

І^п J

Значення ймовірності не перевищити похибку у 10% процедури перевірки студентів складає

р|^L - p < 0,ю|=1 - 0,80 = 0,20.

При цьому повинна виконуватися нерівність правої частини виразу (3.40)

^p^ < 0,20.

пє

Звідси кількість студентів, яких треба перевірити, визначиться як

p(1 - p) 0,90 o (1 - 0,90) 0,90 o 0,10 0,20 -є¹ 0,20 o (0,10)² 0,20 o 0,01

Відповідь: для того, щоб з імовірністю 80% виявити успішно підготовлених студентів з похибкою не вище 10%, треба перевірити більше ніж 45 осіб.

Одним з принципових питань математичної статистики є характер співвідношення параметра є і кількості незалежних випробуваннях п. Відповідь на це питання також дає закон великих чисел.

Приклад 3.17. Для умов прикладу 3.16 оцінити співвідношення кількості незалежних випробувань п і параметра є для трьох значень є (0,1; 0,05; 0,01).

Рішення:

Результати і формули розрахунку п згідно з теоремою Бернуллі (3.40) для різних значень є представлено в табличній формі на рис. 3.29.

Як бачимо з рис. 3.29 (див. стовпчики D і E), при зменшенні параметра е кількість необхідних незалежних випробувань п зростає пропорційно є².

Рис. 3.29. Результати і формули розрахунку n для різних є

Відповідь: чим жорсткіші умови є щодо зменшення різниці між емпіричною частотою події та її теоретичною ймовірністю, тим більшої кількості випробувань потребують такі досліди.

Теорема Чебишева

Теорема Чебишева свідчить: якщо випадкові величини Х, Х₂, X_n попарно незалежні й існує число C таке, що D[Xi < C для всіх /' = 1, 2, n, то для будь-якого є>0 справедлива нерівність

Гxі + x2 +...+Xn _м[xі+м[x2+...+м[Xn 1 с_ ₍₃₄₁₎

[ n n J ne¹

Нерівність (3.41) можна представити інакше

lim p{ - ±X, - - ±M[X, <є} = 1. (3.42)

Отже, ймовірність того, що середнє арифметичне незалежних випадкових ₁n

величин - X X_i відрізняється від середнього арифметичного математичних ₁n

сподівань - X M[X_i менш ніж на є, наближається до 1 при зростанні числа

n ¿=1

випадкових величин, для будь-якого є.

Теорема Чебишева є розвитком і узагальненням теореми Бернуллі Для практичних цілей найчастіше використовується такий варіант випробувань, коли всі X мають однакові показники математичного сподівання МХІ=М і дисперсії DPA^D. Тоді у якості оцінки математичного сподівання використовується вибіркове середнє арифметичне

Формула (3.44) означає, що вибіркове середнє x при збільшені числа випробувань (дослідів, спостережень, вимірювань) як завгодно близько за ймовірністю наближається до свого математичного сподівання М[X]:

x М [ X ]. (3.45)

Отже, вираз (3.45) є доказом того, що вибіркове середнє x є спроможною оцінкою свого аналога з генеральної сукупності. На цьому важливому висновку побудовано статистичне оцінювання (див. розділ 4).

Приклад 3.18. Оцінити ймовірність того, що середнє випадкової величини відхилиться від свого математичного сподівання на значення не більше ніж на три стандартних відхилення.

Рішення:

Визначимо відповідні до теореми Чебишева позначення: x і М[x]- середнє арифметичне величини x і математичне сподівання середнього арифметичного випадкової величини x;

Ж>[ x ] і В[ x ] - стандартне відхилення і дисперсія середнього арифметичного випадкової величини x;

є = 3 o SD[X ] - критерій відхилення різниці х - М[X]|;

рх -М[X]| <є}- ймовірність події, яку треба оцінити з умов задачі.

За теоремою Чебишева маємо рх - М[X]| > г|< ^^Х .

З урахуванням виразу SD[X] = і значення є =3 o SD[X] права час-

тина дорівнюватиме

D[X ] D[X] D[X ] 1 і- -і ) 1

-¹-- =-!-==- =-!-=_- = -, тобто РХ - M[X| >є<-

є² (3 o SD[ X ])² 9 o D[ X ] 9 * ¹ ' 9

З теореми Чебишева можна записати

рх - <г?) = 1 - рх - M[X] >є)< -9.

Тоді ймовірність події, яку треба оцінити, визначиться через нерівність рх - <г}> 1 - -9 = ⁸ * 0,89¹⁷.

Відповідь: ймовірність того, що середнє випадкової величини відхилиться від свого математичного сподівання на значення не більше ніж у три стандартних відхилення, складає приблизно 0,89 або біля 89%.

З теорем Бернуллі і Чебишева як з конкретних форм закону великих чисел випливає той факт, що вибіркові характеристики при зростанні числа випробувань наближаються до теоретичних, що дає можливість оцінювати параметри імовірнісних моделей за емпіричними даними.