В основі застосування методу найменших квадратів покладено умову мінімізації суми квадратів відхилень вибіркових даних від тих, що визначаються оцінкою.
Приклад 4.3. Визначити оцінку генерального середнього /ймнк випадкової величини xза методом найменших квадратів. Рішення:
Згідно з умовою мінімізації можна записати
n
u = £ (x, - її)1 = min. (4.14)
Для визначення екстремуму першу похідну функції u слід прирівняти нулю
-dU- = -l£ (x,-//) = 0, звідки X (xi = Х x, - n<" = 0 і М= - Z xt .
dM ¡=1 i=1 i=1 n ,=1
Отже, /} янк = x. (4.15)
Таким чином, оцінка за методом найменших квадратів математичного сподівання /йянк випадкової величини x є вибіркове середнє x (ця оцінка співпадає з оцінкою максимальної правдоподібності для випадкової величини, що має нормальний розподіл). Метод найменших квадратів має широке застосування у практиці статистичних досліджень, оскільки не вимагає знання закону розподілу випадкової величини і має достатньо розроблений математичний апарат.
Інтервальне оцінювання
Точкові оцінки навіть у тих ситуаціях, коли вони спроможні (наближуються до значення параметру при збільшені n), незміщені (у середньому збігаються з параметром) і ефективні (мають найменшу ступінь випадкових відхилень), є все ж таки наближеними показниками невідомих параметрів. їхнім головним недоліком вважається те, що при малому обсязі вибірки точкові оцінки можуть мати значне розходження з тим параметром, який вони оцінюють, а це може призвести до грубих помилок.
Інтервальною оцінкою називається чисельний інтервал, який покриває21 з певною ймовірністю невідомий параметр генеральної сукупності. Цей чисельний інтервал (2/1) називається довірчим інтервалом, а ймовірність - довірчою ймовірністю в 22. Найчастіше довірчий інтервал вибирається симетричним до параметру ©, тобто (© -а, © +а ).
Розмір довірчого інтервалу залежить від обсягу вибірки п (зменшується з ростом п) і від значення довірчої ймовірності (збільшується при наближенні
в до одиниці). Відхилення оцінки ©п від параметра ©, що оцінюється з певною довірчою ймовірністю в, називають випадковою похибкою репрезентативності. її найбільше відхилення є граничною похибкою. Випадкова похибка репрезентативності виникає внаслідок того, що досліджується не вся сукупність, а лише її частина (вибірка). її не слід плутати з систематичною похибкою репрезентативності, яка є наслідком порушення принципу випадковості при відборі елементів до вибірки, що може мати місце у практичній діяльності.
Довірча ймовірність в визначається дослідником за принципом практичної неможливості, а саме: події з імовірністю, близькою до 1, вважаються вірогідними (достовірними); події з імовірністю, близькою до 0, визнаються невірогідними (неможливими). Цей принцип не може бути доказаний математично. До того ж його сформульовано до однократного виконання випробування.
Поруч із поняттям "довірча ймовірність" в використовується поняття "рівень значущості" а. Між в і а існує співвідношення: в =1- а.
Рівень значущості а - вказує ймовірність помилки оцінювання. Для практичних цілей використовують різні значення довірчої ймовірності в або
21 С.АЙвазян, Н. Кремер та ін. наполягають на використанні саме слів "інтервал покриває", а не "містить", оскільки межі чисельного інтервалу визначаються за вибірковими даними і тому є випадковими величинами [1, С. 289; 41, С. 320].
22 Іноді довірчу ймовірність називають рівнем довіри або надійністю оцінки. [41, С.
320].
рівня значущості а - усе залежить від ризику помилки, який може собі дозволити дослідник. Якщо в (довірча імовірність) - це своєрідний "рівень довіри" прийняття рішення, то сенс параметра а (рівень значущості) можна трактувати як ймовірність ризику помилитися при прийнятті рішення. У психологічних і педагогічних дослідженнях загальноприйнятими вважаються так звані стандартні значення в і а (див. табл. 4.2).
Таблиця 4.2
Стандартні значення довірчої ймовірності в, рівня значущості " і параметра і
Довірча ймовірність | Рівень значущості | Параметр нормального розподілу | |
в | а | 2 а | 2 а/2 |
0,90 (90% вірогідності) | 0,10 (10%-й рівень) | 1,28 | 1,64 |
0,95 (95% вірогідності) | 0,05 (5%-й рівень) | 1,64 | 1,96 |
0,99 (99% вірогідності) | 0,01 (1%-й рівень) | 2,33 | 2,58 |
0,999 (99,9% вірогідності) | 0,001 (0,1%-й рівень) | 3,09 | 3,29 |
Методи визначення довірчих інтервалів реалізовано в основному на двох підходах: на знанні точного розподілу вибіркових характеристик для малих обсягів вибірок і на асимптотичних властивостях розподілу вибіркових характеристик для значних обсягів вибірок.
Довірчий інтервал розміром 2А - це чисельний інтервал, який з довірчою ймовірністю в покриває дійсне значення параметра генеральної сукупності. Наприклад, генеральне середнє /г може належати до інтервалу значень від (X -А) до (X +А), де вибіркове X є серединою цього довірчого інтервалу. Ширина довірчого інтервалу 2А може бути точно обчислена для заданої довірчої ймовірності в (або рівня значущості а) і цілком певного розподілу ймовірностей. На рис. 4.1 показано ширину симетричного довірчого інтервалу генерального середнього /і для нормального розподілу N(0,1).
Як бачимо, при збільшені довірчої ймовірності в (зменшені значення а) ширина довірчого інтервалу 2А зростає, що знижує точність визначення параметра генеральної сукупності. Для нормального розподілу модель інтервальної оцінки середнього генеральної сукупності /и має вигляд:
/ие(Х-А,Х + (4.16)
де А= аІ2Г х ; X і sx - вибіркове середнє і стандартне відхилення; п - обсяг вибірки; 2а/2 - параметр стандартного нормального розподілу (див. табл. 4.2) ; а - рівень значущості - ймовірність того, що відхилення вибіркового від генерального середнього не перевищить А за абсолютним значенням .
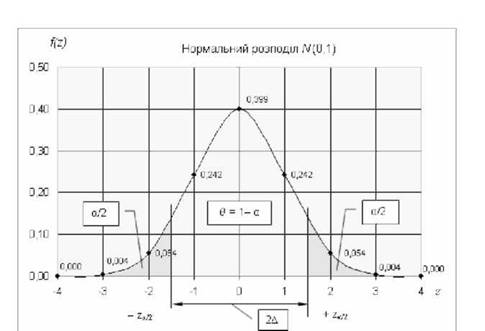
Рис. 4.1. Ширина довірчого інтервалу ТА для середнього /г=0
Вираз (4.16) свідчить, що середнє генеральної сукупності ¡1 покривається
діапазоном значень від (X -А) до (X +А). Оскільки А-то для підвищення
*Jn
точності при заданій довірчій ймовірності слід збільшувати обсяг вибірки n.
Приклад 4.4. Вибірка обсягом 80 осіб має середнє арифметичне X = 100 і стандартне відхилення sx = 5,6. Необхідно оцінити довірчий інтервал середнього генеральної сукупності fi на рівні значущості 0,05.
Послідовність рішення:
o визначити параметр стандартного нормального розподілу для рівня значущості а за допомогою функції MS Excel =НОРМСТОБР(0,05/2), яка повертає значення 1,96;
o довірчий інтервал середнього генеральної сукупності ¡1 дорівнюватиме
Л= = 1,96=56 " 1,23
л/и л/80 '
Відповідь: на рівні значущості 0,05 середнє генеральної сукупності fi належить діапазонові 100,0 + 1,23 . Інакше кажучи, з довірчою ймовірністю 95% середнє fi покривається діапазоном значень у межах від 98,77 до 101,23.
Довірчий інтервал зручно оцінювати за допомогою спеціальної функції MS Excel з відповідними аргументами =ДОВЕРИТ(а; sx; и). Так, для прикладу 4.4, функція =ДОВЕРИТ(0,05; 5,6; 80) повертає вже відоме значення 1,23. Запитання. Завдання.
1. Охарактеризуйте основні методи формування емпіричної вибірки.
2. Розкрийте поняття статистичної оцінки.
3. Чим відрізняються між собою точкове й інтервальне оцінювання?
4. Чим відрізняються "параметри" від " статистик"?
5. Охарактеризуйте основні властивості статистичних оцінок.
6. Яка ідея методу моментів як методи статистичного оцінювання?
7. В чому суть методу максимальної правдоподібності?
8. Які умови покладено в основу методу найменших квадратів?
9. В чому полягає суть інтервального статистичного оцінювання?
10. Охарактеризуйте поняття "довірча ймовірність" і "рівень значущості". Яке співвідношення існує між ними?
11. Що означає довірчий інтервал і як його розрахувати?
12. Повторіть математичні розрахунки за прикладами 4.1 - 4.4.
13. Виконайте лабораторну роботу № 9.
5. ПЕРВІРКА СТАТИСТИЧНИХ ГІПОТЕЗ
5.1. ХАРАКТЕРИСТИКА МЕТОДІВ ПЕРЕВІРКИ СТАТИСТИЧНИХ ГІПОТЕЗ
Поняття статистичної гіпотези
Статистичні критерії
Параметричні і непараметричні критерії
Рівень статистичної значущості
Правила прийняття статистичних рішень
Помилки прийняття статистичних рішень
Статистичні рішення на основі р-значень