Математична статистика - Руденко В.М. - Правила прийняття статистичних рішень

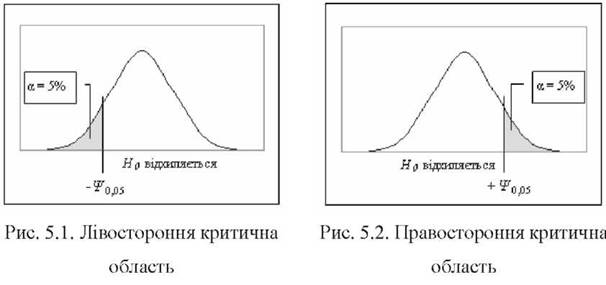
Прийняття статистичних рішень виконується на основі емпіричного критерію: якщо значення ¥_емп знаходяться в критичній області | ¥_емп | > | ¥_кр |, нульова гіпотеза Н₀ відхиляється²⁴. На рис. 5.1 - 5.3 критичні області зафарбовано. Рівень статистичної значущості і відповідні критичні значення критеріїв визначаються по-різному при перевірці спрямованих і неспрямованих статистичних гіпотез. При спрямованих гіпотезах використовується однобічний критерій (рис. 5.1 і 5.2), при неспрямованих - двобічний (рис. 5.3).

Винятки: для деяких непараметричних критеріїв, наприклад, Є-критерію знаків, Т-критерію Вілкоксона і [/-критерію Манна-Вітні встановлюються зворотні співвідношення.

Двобічний критерій строгіший, оскільки він перевіряє відмінності в обидві сторони, і для нього при певному рівні значущості а критичні зони удвічі менші, ніж для однобічного критерію. Отже, на рівні значущості а для однобічного критерію нульова гіпотеза Н₀ відхиляється, коли ¥_емп > ¥ _а , для двобічного критерію Н₀ відхиляється, коли ІРемп > ¥ а/₂ . Наприклад, на рівні значущості а =0,05 критична зона для однобічного критерію складає ¥ _0і05 (рис. 5.1 або 5.2), для двобічного критерію - ¥_{0 025} (рис. 5.3).

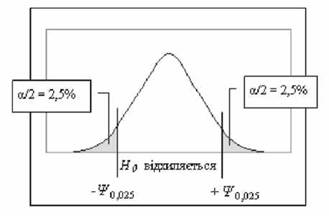
Рис. 5.3. Двостороння критична область

Критичні значення параметричних критеріїв, наприклад, t-критерію Стьюдента або ^-критерію Фішера, зручніше отримувати за допомогою відповідних функцій MS Excel. Критичні значення непараметричних критеріїв табульовано таким чином, що спрямованим гіпотезам відповідає однобічний, а неспрямованим - двобічний критерій. Гіпотези дослідника повинні збігалися за сенсом із гіпотезами, пропонованими в описі кожного з критеріїв.

Помилки прийняття статистичних рішень

Прийняття статистичних рішень супроводжується помилками.

Помилка 1-го роду - це помилка відхилення нульової гіпотези, тоді як вона правильна. Ймовірність такої помилки позначається як а (рівень значущості). Отже, а=р{¥є ¥ _кр | H₀} - це ймовірність події {¥є ¥ кр}, за умови, що нульова гіпотеза Н₀ істина. Якщо ймовірність помилки - це а, то ймовірність правильного рішення (1- а). Чим менше а, тим більша достовірність прийняття правильного рішення.

Помилка 2-го роду - це помилка прийняття нульової гіпотези Н₀ тоді, якщо вона неправильна. Ймовірність помилки 2-го роду позначається як Отже, Р=Р{¥<£ ¥_кр | Н_і} - це ймовірність події {¥<£ ¥кр}, за умови, що альтернативна гіпотеза Н_і прийнята (нульова гіпотеза Н₀ відхилена). Ймовірність не припуститися помилки 2-го роду дорівнює (1- Р) і називається потужністю критерію.

В табл. 5.1 показано можливі помилки прийняття статистичних рішень.

Таблиця 5.і

Помилки прийняття статистичних рішень

Потужність критерію - це його здатність виявляти відмінності, тобто відхиляти нульову гіпотезу про відсутність відмінностей, якщо вона помилкова. Потужність критерію визначається емпіричним шляхом. Виявляється, що деякі критерії дозволяють виявити відмінності там, де інші опиняються неспроможними це зробити, тому пропонується застосовувати більш потужні критерії. Проте підставою для вибору критерію може бути не лише потужність, але й інші його характеристики, а саме: ширший діапазон застосування до даних, визначених, наприклад, за номінальною або ранговою шкалою; обмеженість обсягів вибірки або їхня неоднаковість за обсягом; велика інформативність результатів. Тоді й використовують менш потужні критерії.