Математична статистика - Руденко В.М. - Критерій Шапіро-Вілка W

Критерій х засновано на порівнянні емпіричної гістограми розподілу випадкової величини з її теоретичною щільністю. Діапазон виміряних емпіричних даних розбивають на к інтервалів і розраховують статистику

₂ _ -у (т_і - пр_і)²

Хемп ~ / < ^{, (5.7)}

,=1 ^пр,

де ті - кількість значень випадкової величини, що потрапили в /-й інтервал; п - обсяг вибірки; р_і - теоретична ймовірність випадкової величини потрапити в /-й інтервал.

Для гіпотетичного теоретичного розподілу, який має закон розподілу Р(х), теоретична ймовірність р_і визначається якр_і = Р(х_І+1) - Р(х,), тобто

^рі = |^Р(х)ах = |^Р(х)<1х - |^Р(х)ах = ^Р(х,₊1⁾ - ^Р(х_і⁾. (5.8)

V 1 ₂

За умов к<<п і 2-і - ^{<< п} вважається, що статистика %_емп ^має розподіл

близький до розподілу хі-квадрат для к-1 ступенів вільності. Нульова гіпотеза Н₀ відхиляється на рівні значущості а, якщо хімп > ХІі.

Приклад 5.3. Перевірити за критерієм згоди % гіпотезу про нормальний розподіл емпіричних даних попереднього прикладу 5.2. Послідовність рішення: o Формулювання гіпотез:

Н₀: емпіричний розподіл не відрізняється від нормального; Н_і: емпіричний розподіл відрізняється від нормального.

o Статистичний критерій хімп дорівнює сумі квадратів відхилень емпіричних частот Ші від очікуваних теоретичних частот прі (5.7).

o Послідовність розрахунку емпіричного критерію хімп (результати показано на рис. 5.7, необхідні формули - на рис. 5.8):

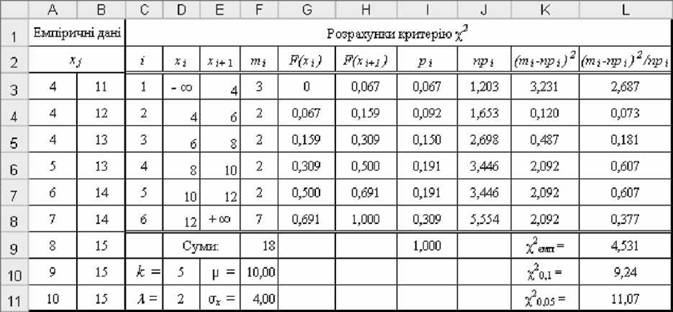
Рис. 5.7. Результати розрахунку критерію %

- внести емпіричні дані у комірки А1:В 11;

- розрахувати кількість класів k за формулою Стерджеса k=1+3,32^-lg(n) Для цього вираз =ОКРУГЛ(1+3,32*ЬОО(СЧЕТ(А3:В11));0) внести у комірку D10 і отримати k=1+3,32lg(18) = 5,2 = 5;

- у комірці D11 розрахувати розмір класового інтервалу X=(x_max-x_min)/k за допомогою виразу =(MAKC(A3:B11)-MHH(A3:B11))/D10 і отримати X ~ 2;

- внести у комірки D3:E8 значення початкових x_i і кінцевих x_i+i границь діапазонів х,- кратними 2. Мінімальне значення першого діапазону становить -оо (комірка D3), максимальне останнього інтервалу +оо (комірка Е8);

- у комірках F3:F8 розрахувати емпіричні абсолютні частоти m_i за допомогою функції =ЧАСТОТА(). Сума частот m_t дорівнюватиме обсягу вибірки, тобто 18;

- теоретична ймовірність випадкової величини p_i потрапити в /'-й інтервал розраховується як різниця значень нормального розподілу F(x_i+1) - F(x,). Значення нормального розподілу можна отримати за допомогою функції MS

Excel = НОРМРАСЩ). Середнє ц і стандартне відхилення а_х теоретичного нормального розподілу внести у комірки F10 i F11 відповідно (зауваження: заміна параметрів нормального розподілу вибірковими статистиками може призвести до суттєвого спотворення статистичних висновків);

- внести у інші комірки відповідні розрахункові вирази за рис. 5.8 і отримати значення емпіричного критерію хімп ,Щ° становитиме 4,53

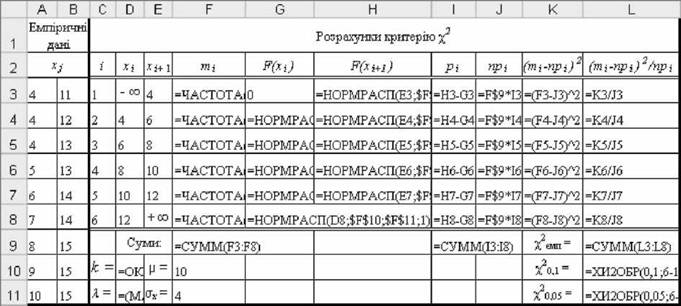
Рис. 5.8. Формули для розрахунку критерію х²_емп

o Критичне значення критерію х²_кр можна отримати за допомогою функції =ХИ20БР(), яка повертає значення двобічного критерію у комірках Е9 і 10 відповідно: -Іо_Л ~ 9,24 і у^о_Д5 ~ 11,07.

o Прийняття рішення. Оскільки /²_еЛИ ~ 4,53 не перевищує критичного значення навіть на рівні а=0,1 (%²о,_і ~ 9,24) , нульова гіпотеза н₀ приймається.

o Формулювання висновків: розбіжності емпіричного і теоретичного нормального розподілів можуть мати винятково випадковий характер.

Перевірку нормальності емпіричного розподілу виконаємо за допомогою критерію Шапіро-Вілка XV.

Критерій Шапіро-Вілка W

Статистика критерію W Шапіро-Вілка має вигляд:

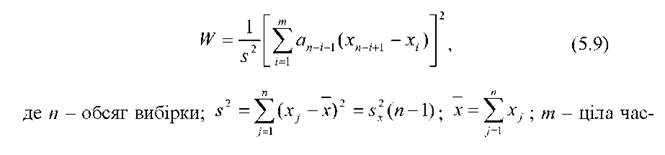
тина 2; коефіцієнти а_пі+1 для невеликих п і /' наведено у табл. 1 Додатків.

Приклад 5.4. Перевірити за критерієм Шапіро-Вілка гіпотезу щодо відповідності нормальному законові розподілу емпіричних даних прикладу 5.2. Послідовність рішення:

o Формулювання гіпотез:.

Н₀: емпіричний розподіл не відрізняється від нормального; Н₁: емпіричний розподіл відрізняється від нормального.

o Послідовність розрахунку емпіричного критерію XV (результати показано на рис. 5.9, необхідні формули - на рис. 5.10):

- у комірках С2:011 розмістити індекси (/') і (п-і+1), причому і змінюється від 1 до ш (ш у прикладі дорівнює п/2 = 18/2 = 9);

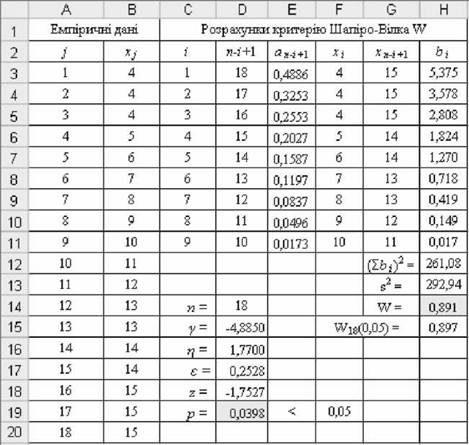
Рис. 5.9. Результати розрахунку Х¥-критерію Шапіро-Вілка

- у комірки Е2:Е11 внести 9 коефіцієнтів з табл. 1 Додатків з рядка для n=18;

- заповнити комірки F2:G11 значеннями x_t i x_n._i+1 або "вручну", або з використанням функцію MS Excel =ВПР(), яка за індексом у лівому стовпчику таблиці повертає значення в тім же рядку із зазначеного стовпця таблиці;

- у комірках H2:H11 розрахувати значення b = a_n__M(x_n__i+1 - Хі );

- у комірці H12 визначити квадрат суми параметрів - (Sb_i)², тобто чисельник виразу (5.9), а у комірці H13 - знаменник - s¹ ;

- значення критерію W у комірці H14 дорівнює (2Ь_і)² / s¹ = 0,891;

- критичне значення критерію W₁₈(0,05) отримати з табл. 2 Додатків. Для n=18 і <х=0,05 це значення складає 0,897 (див. комірку Н15 рис. 5.9).

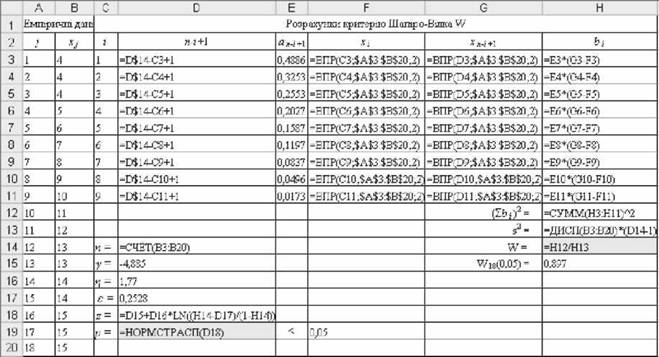
Рис. 5.10. Формули для розрахунку W-критерію Шапіро-Вілка

o Прийняття рішення відбувається за правилом: якщо ¥<¥_п(а), Н₀ відхиляється на рівні 2а. Оскільки XV ~ 0,891 не перевищує критичного значення 0,897 критерію Х¥₁₈(0,05), нульова гіпотеза щодо нормальності розподілу відхиляється на рівні 0,1.

o Формулювання висновків. Розходження між емпіричним і очікуваним теоретичним нормальним розподілами можна вважати статистично значущими на рівні 0,1.

Таким чином, на основі порівняння трьох критеріїв (асиметрії та ексцесу, хі-квадрат, Шапіро-Вілка) можна зробити такі загальні висновки:

- нульові значення моментів у разі застосування критеріїв асиметрії та ексцесу можуть прийматися і для розподілів, відмінних від нормальних. Близькість вибіркових значень асиметрії та ексцесу до теоретичних не обов'язково свідчить про нормальність розподілу результатів спостережень. Ці критерії служать не стільки для перевірки нормальності, скільки для виявлення відхилень розподілу від нормального, або, точніше, для перевірки альтернативних гіпотез [49];

- переважна більшість розподілів спостережень не є нормальними, тому в умовах реальних завдань малоймовірно приймати гіпотезу нормальності. Коректніше стверджувати, що розподіли мало відрізняється від нормального;

- критерій хі-квадрат, як і критерії моментів, не є спроможним. Його доцільно застосовувати лише для відхилення гіпотези нормальності. До того ж, на потужність критерію хі-квадрат сильно впливає кількість (к) і розмір (Я) інтервалів, практично цей критерій можна застосовувати, якщо пр_і > 5;

- кожен критерій має свої "проблеми", існують спеціально розроблені модифікації різних класичних критеріїв, наприклад, типу "хі-квадрат", які можна найбільш ефективно застосовувати у конкретних ситуаціях;

- при розрахунках теоретичного нормального розподілу його параметри (м і а_х) не завжди відомі дослідникові. Заміна їх вибірковими статистиками (X і s_x) може призвести до суттєвого спотворення статистичних висновків;

- найбільш потужним і позбавленим вище перерахованих вад виявився критерій Шапіро-Вілка Ж. За рейтингом цей критерій посідає перше місце серед двадцяти одного аналогічного методу [37, С.278] і може бути рекомендований для перевірки нормальності емпіричних розподілів.

Запитання. Завдання. 1. Які основні недоліки критеріїв асиметрії та ексцесу для перевірки нормальності розподілів?

2. Коли доцільно застосовувати критерію хі-квадрат в завданнях перевірки нормальності розподілів?

3. Проаналізуйте схему вибору параметричних критеріїв залежно від характеру сукупності і досліджуваних завдань.

4. Обґрунтуйте порівняльну характеристику трьох критеріїв (асиметрії та ексцесу, хі-квадрат, Шапіро-Вілка) як засобу оцінки відповідності емпіричного розподілу нормальному законові.

5. Повторіть математичні процедури завдань за прикладами 5.1 і 5.4.

6. Виконайте лабораторну роботу № 10.