Математична статистика - Руденко В.М. - Значущість середнього (критерій t, дисперсія невідома)

Критерій Стьюдента t використовується для перевірки гіпотез про чисельне значення середнього параметра з нормальним законом розподілу, коли дисперсія сукупності є невідомою.

Приклад 5.11. Мета вибіркового тестування 40 учнів (таблиця рис. 5.26) -оцінити показники успішності у навчанні за новою методикою. Чи можна на рівні значущості 0,05 прийняти, що результати тестування перевищать середній нормативний показник у 4,0 бали?

Послідовність рішення:

o Ситуації відповідає варіант спрямованих гіпотез:

Ні: р > /г₀.

o Перевірка припущень: досліджуваний параметр має нормальний розподіл; дисперсія невідома; виміри зроблено за шкалою інтервалів.

o Вибір статистичного критерію. Згідно з припущеннями цій ситуації відповідає однобічний і-критерій:

, ₌ ^^4^п^1, (5.20)

^Js

де ¡1 - середнє генеральної сукупності; ц₀, 8² і п - середнє, дисперсія та обсяг вибірки.

o Результати розрахунку емпіричного і-критерію і_емп показано на рис. 5.26, необхідні формули - на рис. 5.27. Емпіричне значення і-критерію:

і"" = І^Т^ - 2,09.

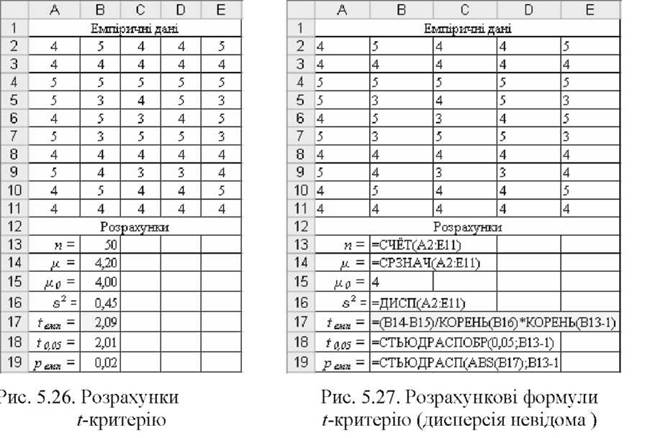
o Визначення критичного значення і-критерію можна здійснити за допомогою функції =СТЬЮДРАСПОБР(), аргументами якої є рівень значущості а і число ступенів вільності а⁷/ = п-1. Для значень а = 0,05 а⁷/= 50-1 = 49 функція =СТЬЮДРАСПОБР() повертає значення однобічного критерію відповідно до варіанту спрямованих гіпотез: ґ₀₀₅ -2,01.

o Прийняття рішення. Оскільки |і_еЛИ| > ґ_0>05 , тобто (2,09 > 2,01), нульова гіпотеза Н₀ відхиляється на рівні значущості 0,05.

o Формулювання висновків. На рівні значущості 0,05 можна стверджувати, що результати тестування перевищують нормативний показник у 4,0 бали. Пропонуємо також самостійно розібратися у значенні й сенсі ймовірності р_емп (див. комірку В19 рис. 5.27).

Значущість дисперсії (критерій х²)

У дослідженнях з психології і педагогіки мають місце завдання, коли необхідно оцінити властивості варіативності параметрів. Для таких ситуацій використовуються методи перевірки статистичних гіпотез щодо дисперсій сукупностей. Передбачається, що інтервальні дані мають нормальний закон розподілу.

Приклад 5.12. Чи можна стверджувати про те, що вибірка взята із генеральної сукупності з дисперсією (т₀²=0,25 (дані наведено у таблиці рис. 6.24)? Послідовність рішення:

o Формулювання неспрямованих гіпотез: Щ: а² = 0,25;

Н1: а² ф 0,25.

o Перевірка припущень: досліджуваний параметр має нормальний розподіл; виміри зроблено за шкалою інтервалів.

o Вибір статистичного критерію. Згідно з припущеннями цій ситуації відповідає модель двобічного /²-критерію:

2 (п-1) o ^

x = "-, (5.21)

^СТ0

де п - обсяг вибірки; 8_Х - дисперсія вибірки. o Результати розрахунку емпіричного критерію /²_ем" показано на рис. 5.28, необхідні для цього формули - на рис. 5.29. Значення вибіркової дисперсії дорівнює: s_x²=0,44. Значення емпіричного критерію /²_ем" таке:

₌ ⁽³⁰ -¹⁾ o^0,44 _т 5120 Х_емп 0,25 ~^51,20.

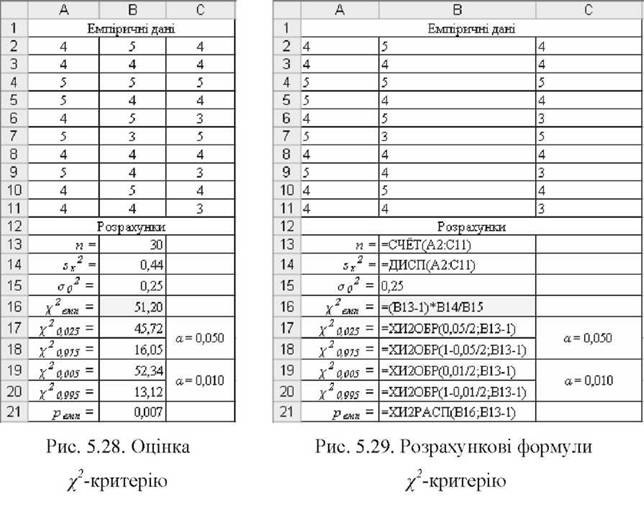
o Критичне значення критерію х Д^ля двобічної моделі на рівні значущості а встановлюються для точок (а/2) і (1- а/2) розподілу х², який є похідним від нормального, з числом ступенів вільності df = n-1. Значення /²_а/2 і /²₁._а/2 можна отримати за допомогою функції MS Excel =ХИ20БР(). Для а=0,05 і df=29 функція повертає: х₀₂₅ ~ 45,72 і /²_0,975 ~ 16,05; для а=0,01 - відповідно: /²0,005 ~ 52,34 І /²0,995 ~ 13,12.

o Прийняття рішення. Оскільки для рівні значущості 0,05 /²_ем" знаходиться у критичній зоні Хемп> Х²0,025 > X 0,975 (51,20 > 45,72 > 16,05), нульова гіпотеза H₀ відхиляється. Проте на рівні значущості 0,01 нульова гіпотеза H₀ приймається, оскільки х²₀,₀₀₅ > X гм я> Х²₀,₉₉₅, тобто умова 52,34 > 51,20 > 13,12 виконується.

o Формулювання висновків. На рівні значущості 0,01 є підстави стверджувати про те, що вибірка належить генеральній сукупності. Про це також свідчить ймовірність р_ем", яку можна отримати за допомогою функції MS Excel =ХИ2РАСП(), яка повертає однобічну ймовірність р_ем" = 0,007 розподілу /². Отже, нульова гіпотеза H₀ приймається лише на рівні значущості а =0,01, оскільки виконується умова а/2< р_ем" (0,01/2=0,005<0,007). Пропонуємо самостійно проаналізувати отримані результати.