Математична статистика - Руденко В.М. - Відмінності у значеннях дисперсій (F-критерій Фішера для двох незв'язаних вибірок )

Процедури перевірки гіпотез про рівність середніх для двох незалежних (незв'язаних) вибірок на основі критерію Стьюдента і продемонстровано у розділі 5.3, формула (5.10). Для двох зв'язаних вибірок, якщо є природна парність спостережень, наприклад, тестування об'єктів двічі - до та після експерименту, використовується так званий двовибірковий і-критерій Стьюдента. Статистика критерію має вигляд:

2 o а _г

і =-<п , (5.22)

де а =¹V а_і - середнє різниць; п - обсяг вибірки; ^ = (х_і1 - х_і2) - різни-п

|Х(а - а,)²

ця значень; х_а - ,1---- стандартне відхилення а,. Для статистики не

V п - 1

передбачається рівність дисперсій сукупностей, з яких обрано дані.

Приклад 5.13. Чи можна стверджувати на рівні значущості 0,05 (0,01) про те, що середні показники вибірки до і після експериментальної дії відрізняються одне від одного? Емпіричні дані представлено на рис. 5.30.

Послідовність рішення:

o Формулювання гіпотез:

Н₀: ц₁ - ц₂ = 0 (р₁ не відрізняється від /г₂); Н₁: ц₁ - ц₂ ф 0 (р₁ відрізняється від /г₂).

o Перевірка припущень: досліджуваний параметр має нормальний розподіл; дисперсії сукупностей невідомі; вибірки зв'язані; виміри за шкалою відношень.

o Вибір статистичного критерію. Згідно з припущеннями умовам відповідає модель двобічного і-критерію Стьюдента для зв'язаних вибірок:

2 o а _Г

o Результати розрахунку емпіричного критерію і_емп показано на рис. 5.30, необхідні для цього формули - на рис. 5.31. Емпіричне значення критерію дорівнює:

і = --^./Гї . 3,87 "™ 0,47 ^.

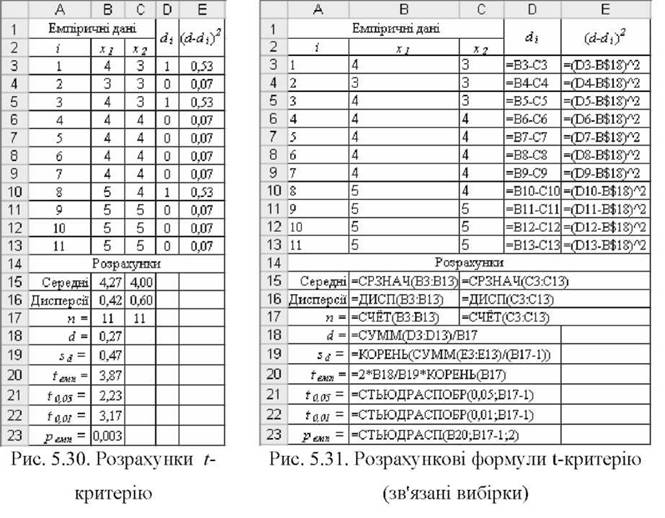
o Визначення критичного значення двобічного t-критерію Стьюдента можна виконати за допомогою функції =СТЬЮДРАСПОБР(). Для прийнятого рівня значущості а=0,05 (0,01) і ступенів вільності df= "-1=11-1=10 критичне значення дорівнюватиме: t_0i05~ 2,23 (t_0i01 ~ 3,17).

o Прийняття рішення. Оскільки t_eMn > t_0>01 (3,87 > 3,17), нульова гіпотеза Н₀ відхиляється на рівні значущості 0,01.

o Формулювання висновків. Підстави стверджувати про те, що показники вибірок не відрізняються одне від одного, відсутні на рівні значущості 0,01.. Пропонуємо самостійно прокоментувати значення показника р_ем".

Відмінності у значеннях дисперсій (F-критерій Фішера для двох незв'язаних вибірок )

Порівняння дисперсій двох сукупностей набагато цікавіше, аніж завдання перевірки відповідності дисперсії деякому передбачуваному значенню. Для перевірки гіпотези про рівність дисперсій двох незалежних сукупностей використовується критерій Фішера F, статистика якого має вид:

F = si² / S2², (5.23)

де s₁² і s₂²- дисперсії вибірок.

При цьому обсяги вибірок можуть бути як однакові, так і різні. Приклад 5.14. Чи можна стверджувати, що показники вибіркових дисперсій за даними рис. 5.32 статистично не відрізняються одне від одного? Послідовність рішення:

o Формулювання гіпотез. Умовам перевірки однаковості дисперсій а²₁ і & отриманих із двох сукупностей, відповідає варіант неспрямованих гіпотез:

Н₀: а²₁ = а²₂ (а²₁ не відрізняється від а²ф); Н₁: а²₁ Ф а²₂ (а²₁ відрізняється від а²ф).

o Перевірка припущень: досліджуваний параметр має нормальний розподіл; вибірки незв'язані; виміри зроблено за шкалою інтервалів.

o Вибір статистичного критерію. Ситуації відповідає модель двобічного

Б-критерію Фішера: Г_ем" = 8² / 8₂.

o Результати розрахунку ¥_гмп показано на рис. 5.32, необхідні для цього формули - на рис. 5.33. Дисперсії вибірок 8² ~ 1,54 8₂~ 0,70. Звідси значення емпіричного критерію таке: ¥_гмг= 1,54/0,70 ~ 2,21.

o Визначення критичного значення критерію Б. Для двобічної моделі на рівні значущості а встановлюються два критичні значення Г_кр для точок (а/2) і (1- а/2) Б-розподілу, тобто: Б_а/2 і Б₁._а/2 з числом ступенів вільності = п₁ -1= 14-1=13 і ¿#2 = п₂ - 1= 16-1=15,

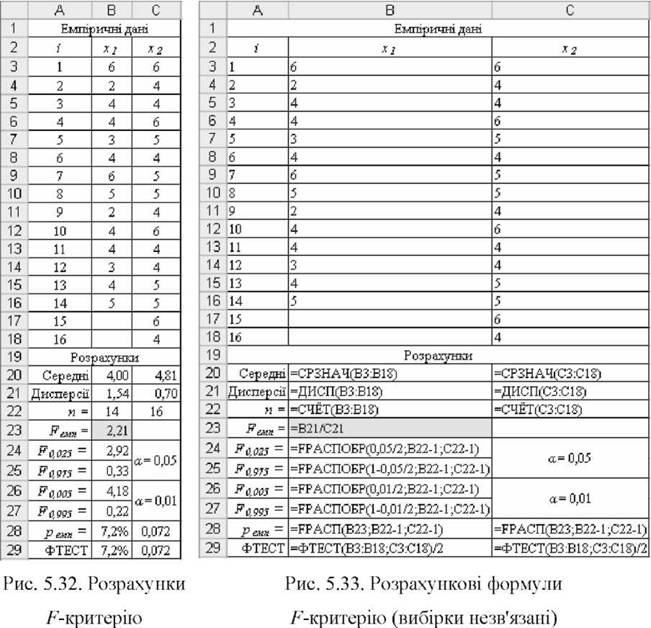
Для прийнятого рівня значущості а і ступенів вільності а/1 і а/₂ критичні значення двобічного критерію можна отримати за допомогою функції =РРАСПОБР(). Для а = 0,05 отримаємо 7^₀₂₅ = 2,92 і 7^₉₇₅ ~ 0,33; для а = 0,01 критичні значенняF_{0 005} ~ 4,18 і F_{0 995} ~ 0,22.

o Прийняття рішення. Оскільки значення f_eMrp 2,21 не знаходиться у жодній критичній зоні (0,33 < 2,21 < 2,92), приймається нульова гіпотеза Н₀.

o Формулювання висновків. Навіть на рівні значущості 0,05 немає підстав стверджувати про те, що показники дисперсій відрізняються одне від одного.

Перевірку статистичних гіпотез про істотність різниці дисперсій двох не-зв'язаних вибірок можна провести шляхом оцінювання ймовірності р_ем" за допомогою функції =FPACn(B23;B22-1;C22-1), яку внесено у комірку В28 (див. рис. 5.32 і 5.33). Як бачимо, р_ем" ~ 0,072 (7,2%). Нульова гіпотеза н₀ приймається за умови р_ем" > а. У нашому прикладі навіть на рівні значущості а =0,05(5%) ця умова виконується: 7,2% > 5%. Це значить, що нульова гіпотеза н₀ повинна бути прийнята, як це зроблено вище.

Експрес-оцінювання можна провести за допомогою функції MS Excel =3>TECT(B3:B18;C3:C18)/2, яку внесено у комірку В29 (див. рис. 5.32 і 5.33). Оскільки функція повертає однобічну ймовірність однаковості двох сукупностей, для двобічної ймовірності слід брати її половину. Аргументами функції виступають вибіркові масиви. Для двобічної моделі нульова гіпотеза н₀ приймається на рівні значущості а, якщо виконується умова а < ФТЕСТ < 1- а.

У нашому прикладі навіть на рівні значущості а=0,05 (5%) умова 5%<7,2%<95% виконується, а це значить, що н₀ приймається.

Перевірку статистичних гіпотез щодо різниці дисперсій можна виконати за допомогою пакета "Аналіз даних" розділ "Двовибірковий F-тест для дисперсій" (рис. 5.34).

Рис. 5.34. Меню пакета "Аналіз даних"

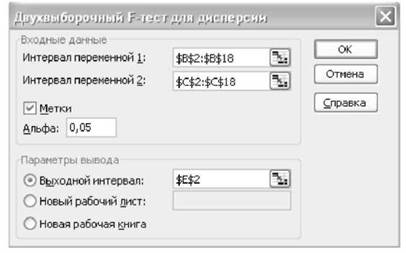
Для цього у діалоговому вікні необхідно ввести параметри, як показано на рис. 5.35, виконати команду "ОК" і отримати результати (рис. 5.36).

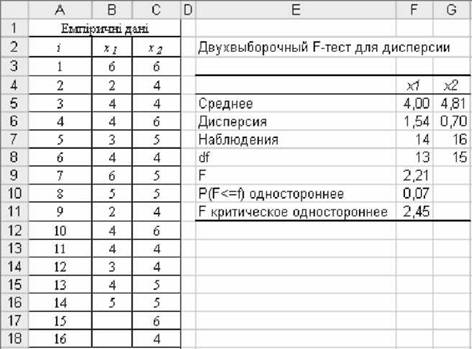
Рис. 5.35. Діалогове вікно "Двовибірковий Р-тест для дисперсій"

Рис. 5.36. Результати двовибіркового Р-тесту

Комп'ютерний засіб виконує розрахунки основних статистик (середні, дисперсії), а також значення емпіричних і теоретичних ^-критеріїв, які дозволяють зробити висновки щодо різниці дисперсій на рівні значущості а.