Математична статистика - Руденко В.М. - 6. ДИСПЕРСІЙНИЙ АНАЛІЗ

Основною метою дисперсійного аналізу, фундаментальна концепція якого була запропонована Фішером у 1920 р., є дослідження значущості відмінності між середніми декількох груп даних або змінних. Якщо порівнюються середні двох груп, дисперсійний аналіз дасть той же результат, що і звичайний ґ-критерій для незалежних або залежних вибірок. Проте використання дисперсійного аналізу має переваги особливо для малих вибірок.

У дисперсійному аналізі перевірка статистичної значущості відмінності між середніми декількох груп здійснюється на основі вибіркових дисперсій. Ця перевірка проводиться за допомогою розбиття загальної дисперсії (варіації) на частини, одна з яких обумовлена випадковою помилкою (тобто внут-рішньогруповою мінливістю), а друга пов'язана з відмінністю середніх значень. Якщо ця відмінність значуща, нульова гіпотеза щодо існування відмінності між середніми значеннями відкидається на певному рівні значущості.

Дисперсійний однофакторний аналіз

Дисперсійний однофакторний аналіз використовується у дослідженнях зміни результативної ознаки під впливом зміни умов або градацій фактора. Суть математичних перетворень дисперсійного методу полягає в тому, щоб зіставити дисперсії за факторами із дисперсією усіх значень, отриманих в експерименті. Однофакторний аналіз вимагає не менше трьох градацій фактора і не менше двох випробовувань у кожній градації. При проведенні дисперсійного аналізу необхідно перевірити нормальність розподілу досліджуваної випадкової величини і відсутність відмінності дисперсій сукупностей. Це можна виконати методами перевірки статистичних гіпотез (див.розділ 5).

Припустимо, що аналізується вплив фактора А на к рівнях А₁, ^4₂, А_к. Наприклад, в експерименті це можна реалізувати, якщо задіяти к вибірок з різними градаціями умов. На кожному рівні Лі (для кожної вибірки) проведено п спостереженьх_/1, х_/2, х_іп (див. табл. 6.1).

Таблиця 6.1

Розглянемо оцінки різних дисперсій.

Дисперсія я² для рівня Аі (для певної вибірки) може бути записана як

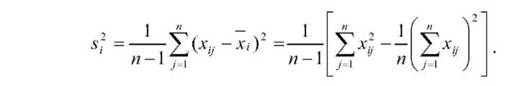
Дисперсія я₀ , що характеризує варіативність поза впливу фактора А

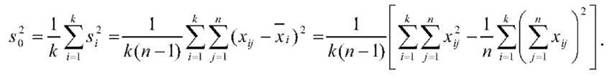
Загальна дисперсія я всіх пк спостережень дорівнює

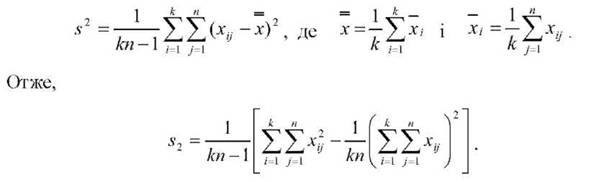
Дисперсія я ²_А, що характеризує зміну середніх х/ під впливом фактора А:

1 к _ =

^к ~ ¹ ¡=1

Перевірка впливу фактора А на зміну середніх може бути зведена до порівняння дисперсій я²_А і я² . Вплив фактора А вважатиметься значущим на ріні

а, якщо є значущим відношення 5 1я², тобто якщо

5²_Л і^ > ^_а[к -1; к(п -1)], де к -1; к(п -1) - ступені вільності ^-розподілу, 5 і я⁷] - ^-критерій Фішера. Приклад 6.1. Довести припущення про те, що фактор швидкості пред'явлення слів впливає на показники їх відтворення (дані у таблиці рис. 8.1). Послідовність рішення:

o Формулювання гіпотез.

Н₀: фактор швидкості не є більш вираженим, ніж випадковим; Н₁: фактор швидкості є більш вираженим, ніж випадковим.

o Перевірка припущень: досліджуваний параметр має нормальний розподіл; вибірки незв'язані однакових обсягів; виміри за шкалою відношень.

o Визначення емпіричного критерію Г_емп базується на зіставленні квадратів сум по стовпцях із сумою квадратів усіх емпіричних значень. Кожний стовпець представляє вибірку і відповідає певній градації фактора швидкості.

o Введені позначення:

п = 6 - кількість спостережень (рядків);

к = 3 - кількість факторів (стовпчиків);

пк = 6-3 = 18 - загальна кількість індивідуальних значень;

7 - індекс рядків змінюється від 1 до п (7 =1, 2, ..., п);

і - індекс стовпчиків змінюється від 1 до к (і =1, 2, ..., к).

o Математичні розрахунки (див. рис 6.1 і 6.2):

- розрахувати суми в комірках В13:В15 за формулами

і=1 7=1 п _м кп ^ і₌1 )

а саме

Є₁ = 6² + 7² + 6² + 5² +_+5² +5² = 432; й₂ = --(34² + 29² + 23²) = 421;

6

й₃ ^^(34 + 29 + 23)² = 410,89; 3 o 6

- розрахувати емпіричний критерій ¥_гмп в комірці В16 за формулою

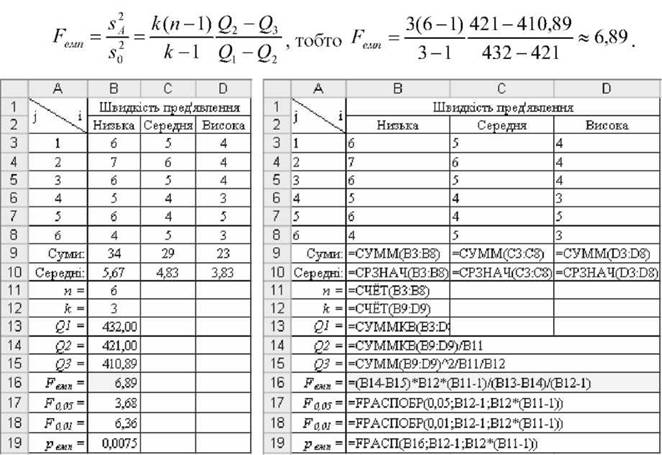
Рис. 6.1. Результати Рис. 6.2. Розрахункові формули

дисперсійного аналізу однофакторного дисперсійного аналізу

o Критичне значення ^_кр можна отримати за допомогою функції

=РРАСПОБР() для рівня значущості для а = 0,05 (0,01) і числа ступенів вільності к -1 = 3-1=2 і к(п -1) = 3(6-1)=15. Г_0і05 ~ 3,68 і Г_0і01 ~ 6,36.

o Прийняття рішення. Оскільки ¥_гмп >Р_0?01 (6,89 > 6,36), нульова гіпотеза Н₀ відхиляється на рівні значущості 0,01.

o Формулювання висновків. Відмінності в обсязі відтворення слів (фактор швидкості) є більш вираженими, ніж випадковим. Цю залежність можна представити графічно на рис. 6.3.

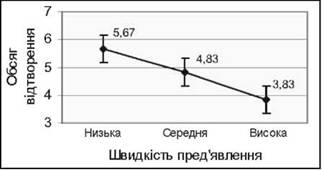
Рис. 6.3. Залежність середнього обсягу відтворених слів від швидкості пред'явлення

Розрахунки однофакторної моделі можна провести за допомогою пакета "Аналіз даних" розділ "Однофакторний дисперсійний аналіз" (рис. 6.4).

Рис. 6.4. Меню пакета "Аналіз даних" Після введення відповідних параметрів (рис. 6.5) можна отримати результати однофакторного дисперсійного аналізу (рис. 6.6).

Рис. 6.5. Діалогове вікно

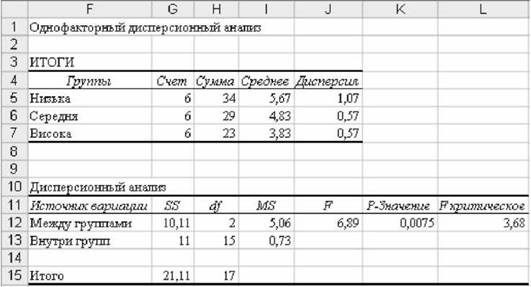
Рис. 6.6. Результати однофакторного дисперсійного аналізу (а = 0,05)

Комп'ютерний пакет "Аналіз даних" виконує розрахунки основних статистик (суми, середні, дисперсії, значення емпіричних і теоретичних критеріїв тощо), що дає підстави дослідникові для статистичних висновків.