Теорія статистики - Мармоза А.Т. - Розділ 4. Середні величини

4.1. Поняття про середні величини

Статистична сукупність складається з множини одиниць, об'єктів або явищ однорідних в деякому відношенні і одночасно відмінних за величиною ознак. Величина ознаки кожного об'єкта визначається як загальними для всіх одиниць сукупності, так і індивідуальними її особливостями.

Аналізуючи впорядковані ряди розподілу (ранжировані, інтервальні та ін.), можна помітити, що елементи статистичної сукупності явно концентруються навколо деяких центральних значень. Така концентрація окремих значень ознаки навколо деяких центральних значень, як правило, має місце у всіх статистичних розподілах. Тенденцію окремих значень досліджуваної ознаки групуватися навколо центра розподілу частот називають центральною тенденцією. Для характеристики центральної тенденції розподілу застосовуються узагальнюючі показники, які отримали назву середніх величин.

Середньою величиною у статистиці називають узагальнюючий показник, який характеризує типовий розмір ознаки в якісно однорідній сукупності в конкретних умовах місця і часу та відображає величину варіюючої ознаки з розрахунку на одиницю сукупності. Обчислюється середня величина у більшості випадків шляхом ділення загального обсягу ознаки на число одиниць, що володіють цією ознакою. Якщо, наприклад, відомий фонд місячної заробітної плати і кількість робітників за місяць, то середню місячну заробітну плату можна визначити шляхом ділення фонду заробітної плати на кількість робітників.

В якості середніх величин виступають такі показники як середня тривалість робочого дня, тижня, року, середній тарифний розряд робітників, середній рівень продуктивності праці, середній національний доход на душу населення, середня врожайність зернових культур по країні, середнє споживання продуктів харчування на душу населення тощо.

Середні величини обчислюються як з абсолютних, так і з відносних величин, є показниками іменованими і виражаються в тих самих одиницях вимірювання, що і усереднювана ознака. Вони характеризують одним числом значення досліджуваної сукупності. В середніх величинах знаходить відображення об'єктивний і типовий рівень соціально-економічних явищ і процесів.

Кожна середня характеризує досліджувану сукупність за однією будь-якою ознакою, але для характеристики будь-якої сукупності, опису її типових рис і якісних особливостей потрібна система середніх показників. Тому у практиці вітчизняної статистики для вивчення соціально-економічних явищ, як правило, використовується система середніх показників. Так, наприклад, показники середньої заробітної плати оцінюються спільно з показниками продуктивності праці (середнього виробітку продукції за одиницю робочого часу), фондоозброєністю і енергоозброєністю, рівнем механізації та автоматизації робіт та ін.

У статистичній науці і практиці середні величини мають виключно велике значення. Метод середніх величин є одним з найважливіших статистичних методів, а середня величина - однією з основних категорій статистичної науки. Теорія середніх величин займає одне з центральних місць в теорії статистики. Середні величини є основою для розрахунку показників варіації (розділ 5), помилок вибірки (розділ 6), дисперсійного (розділ 8) і кореляційного аналізу (розділ 9).

Не можна уявити також статистику без індексів, а останні по суті являють собою середні величини. Використання методу статистичних групувань теж веде до користування середніми величинами.

Як уже зазначалося, метод групувань - один із з основних методів статистики. Метод середніх у поєднанні з методом групувань це складова частина науково розробленої статистичної методології. Середні показники органічно доповнюють метод статистичних групувань.

Середні величини використовуються для характеристики зміни явищ в часі, розрахунку середніх темпів зростання і приросту. Наприклад, зіставлення середніх темпів зростання показників продуктивності праці та її оплати за певний період (ряд років) розкриває характер розвитку явищ за досліджуваний проміжок часу, окремо продуктивності праці і окремо оплати праці. Зіставлення темпів зростання зазначених двох явищ дає уяву про характер і особливість співвідношення зростання чи зниження продуктивності праці щодо її оплати за певні проміжки часу.

У всіх випадках, коли виникає потреба охарактеризувати одним числом сукупність значень ознаки, що змінюються, користуються його середнім значенням.

В статистичній сукупності значення ознаки змінюється від об'єкта до об'єкта, тобто варіює. Усереднюючи ці значення і надаючи урівняне значення ознаки кожному члену сукупності ми абстрагуємось від індивідуальних значень ознаки, тим самим якби замінюємо ряд розподілу значень ознаки одним і тим самим значенням, рівним середній величині. Однак така абстракція правомірна лише в тому випадку, якщо усереднення не змінює основної властивості по відношенню до даної ознаки в цілому. Ця основна властивість статистичної сукупності, пов'язана з окремими значеннями ознаки, і яка при усередненні має бути збережена незмінною, називається визначальною властивістю середньої по відношенню до досліджуваної ознаки. Інакше кажучи, середня замінюючи індивідуальні значення ознаки, не повинна змінювати загального обсягу явища, тобто обов'язкова така рівність: обсяг явища дорівнює добутку середньої величини на чисельність сукупності. Наприклад, якщо з трьох значень урожайності ячменю (х, =20,0; 23,3; 23,6 ц/га) обчислена середня (20,0+23,3+23,6):3 = 22,3 ц/га, то за визначальною властивістю середньої має бути дотримана така рівність:

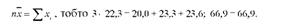
Як видно з наведеного прикладу, середня врожайність ячменю не співпадає з жодною з індивідуальних, так як ні в одному господарстві не одержана врожайність 22,3 ц/га. Проте якщо уявити, що в кожному господарстві одержали по 22,3 ц/га, то загальна сума врожайності не зміниться і буде дорівнювати 66,9 ц/га. Отже, середня замінюючи фактичне значення окремих індивідуальних показників, не може змінити розмір всієї суми величин досліджуваної ознаки.

Головне значення середніх величин полягає в їх узагальнюючій функції, тобто заміні множини різних індивідуальних значень ознаки середньою величиною, яка характеризує всю сукупність явищ. Властивість середньої характеризувати не окремі одиниці, а виразити рівень ознаки з розрахунку на кожну одиницю сукупності є її відмінною спроможністю. Ця особливість робить середню узагальнюючим показником рівня варіюючої ознаки, тобто показником, який абстрагується від індивідуальних значень розміру ознаки у окремих одиниць сукупності. Але те, що середня є абстрактною, не позбавляє її наукового дослідження. Абстракція є необхідна ступінь всякого наукового дослідження. В середній величині, як у будь-якій абстракції, здійснюється діалектична єдність індивідуального і загального. Взаємозв'язок середніх і окремих значень усереднюваної ознаки служить вираженням діалектичного зв'язку індивідуального і загального.

Застосування середніх має базуватися на розумінні та взаємозв'язку діалектичних категорій загального і індивідуального, масового і одиничного.

Середня величина відображає те загальне, що складається в кожному окремому, одиничному об'єкті. Завдяки цьому середня отримує велике значення для виявлення закономірностей, притаманних масовим суспільним явищам і не помітних в одиничних явищах.

У розвитку явищ необхідність поєднується з випадковістю. Тому середні величини пов'язані із законом великих чисел. Суть цього зв'язку полягає в тому, що при розрахунку середньої величини випадкові коливання, що мають різну спрямованість, в силу дії закону великих чисел, взаємно урівноважуються, погашаються і у величині середньої чітко відображається основна закономірність, необхідність, вплив загальних умов, характерних для даної сукупності. В середній знаходить відображення типовий, реальний рівень досліджуваних явищ. Оцінка цих рівнів і зміна їх в часі і просторі - одне з головних завдань середніх величин. Так, через середні виявляється, наприклад, закономірність підвищення продуктивності праці, урожайності сільськогосподарських культур, продуктивності тварин. Отже, середні величини являють собою узагальнюючі показники, в яких знаходить своє відображення дія загальних умов, закономірність досліджуваного явища.

За допомогою середніх величин вивчають зміну явищ у часі і просторі, тенденції в їх розвитку, зв'язки і залежності між ознаками, ефективність різних форм організації виробництва, праці і технологій, впровадження науково-технічного прогресу, виявлення нового, прогресивного в розвитку тих чи інших соціально-економічних явищ і процесів.

Середні величини широко застосовуються в статистичному аналізі соціально-економічних явищ, так як саме в них знаходять своє виявлення закономірності і тенденції розвитку масових суспільних явищ, варіюючих як у часі, так і у просторі. Так, наприклад, закономірність підвищення продуктивності праці в економіці знаходить своє відображення в зростанні середнього виробництва продукції з розрахунку на одного працівника, зайнятого у виробництві, збільшення валових зборів - у зростанні середньої урожайності сільськогосподарських культур тощо.

Середня величина дає узагальнену характеристику досліджуваного явища тільки за однією ознакою, яка відображає одну з найважливіших його сторін. У зв'язку з цим для всебічного аналізу досліджуваного явища необхідно будувати систему середніх величин за рядом взаємопов'язаних і доповнюючих один одного суттєвих ознак.

Для того, щоб середня відображала дійсно типове і закономірне в досліджуваних суспільних явищах при її розрахунку необхідно дотримуватись таких умов.

1. Ознака, за якою обчислюється середня має бути істотною. В противному разі буде отримана несуттєва або спотворена середня.

2. Середню потрібно обчислювати тільки за якісно однорідною сукупністю. Тому безпосередньому обчисленню середніх має передувати статистичне групування, яке дає змогу розчленувати досліджувану сукупність на якісно однорідні групи. У зв'язку з цим науковою основою методу середніх величин є метод статистичних групувань.

Питання про однорідність сукупності не повинне вирішуватися формально за формою її розподілу. Його, так само як і питання про типовість середньої, потрібно вирішувати, виходячи з причин і умов, що формують сукупність. Однорідною є та сукупність, одиниці якої формуються під впливом загальних головних причин і умов, які визначають загальний рівень даної ознаки, характерний для всієї сукупності.

3. Розрахунок середньої величини має базуватися на охопленні всіх одиниць даного типу або досить великої сукупності об'єктів, щоб випадкові коливання взаємно зрівноважували один одного і проявлялася закономірність, типові і характерні розміри досліджуваної ознаки.

4. Загальною вимогою при розрахунку будь-якого виду середніх величин є обов'язковим збереження незмінним загального обсягу ознаки в сукупності при заміні індивідуальних її значень середнім значенням (так звана визначальна властивість середньої).