Теорія статистики - Мармоза А.Т. - 6.4. Визначення необхідної чисельності вибірки

При організації вибіркового спостереження виникає питання про те, якою повинна бути чисельність вибіркової сукупності, при якій межі можливої помилки не перевищать деякої заздалегідь заданої дослідником величини. Необхідно встановити таку чисельність вибірки, яка з довірчим рівнем імовірності Р забезпечувала б одержання даних, що достатньо повно відображають узагальнюючі характеристики генеральної сукупності.

Надто велика вибірка призведе до нераціональних витрат трудових і матеріальних коштів, а недостатня - до великих помилок. Отже, треба встановити оптимальну чисельність вибірки, яка б гарантувала потрібну точність результатів і надійність висновків спостереження.

Необхідна чисельність вибірки залежить від таких факторів:

1. Розміру граничної помилки вибірки єр, тобто величини можливих відхилень показників генеральної сукупності від показників вибіркової сукупності. Чим менше розмір заданої граничної помилки, тим більшою має бути чисельність вибірки.

При визначенні необхідної чисельності вибірки гранична помилка вибірки заздалегідь задається самим дослідником залежно від характеру вирішуваних завдань і потрібної точності висновків. На практиці звичайно виходять з того, що гранична помилка вибірки по відношенню до середньої помилки не перевищує 1-5%. Іншими словами, цей процент не повинен перевищувати прийнятий довірчий рівень значущості а.

2. Ступеня варіації досліджуваної ознаки. Чим більше варіація (дисперсія, коефіцієнт варіації та ін.,), тим більшою має бути чисельність вибірки.

3. Рівня довірчої імовірності Р, з яким потрібно гарантувати припустимі розміри граничної помилки вибірки. Імовірність у свою чергу пов'язана з нормованим відхиленням і. Чим більшим є заданий рівень довірчої імовірності Р, тим більше нормоване відхилення і, тим більшою має бути чисельність вибіркової сукупності.

4. Способу відбору одиниць у вибіркову сукупність (повторний або безповторний відбір).

Отже, при визначенні необхідної чисельності вибірки мають бути задані такі умови: а) розмір граничної помилки; б) рівень варіації (дисперсія, коефіцієнт варіації та ін.); в) рівень довірчої імовірності і значення нормованого відхилення, що відповідає їй.

Формули для розрахунку необхідної чисельності вибірки виводяться з формул граничних помилок для середньої і для частки шляхом відповідних алгебраїчних перетворень:

Наведемо формули необхідної чисельності вибірки для різних способів відбору;

а) при визначенні середнього розміру ознаки і о

п = £2 - власне випадкова і механічна повторна вибірка;

При обчисленні необхідної чисельності вибірки потрібно знати міру коливання досліджуваної ознаки. Однак, дисперсія ознаки або її частка р у генеральній сукупності, як правило, невідомі і визначатимуться лише після проведення вибіркового спостереження. Не знаючи цих величин, не можна визначити необхідну чисельність вибірки.

Труднощі, що виникають, можна розв'язати такими шляхами:

1. Замість фактичного значення а0 або р підставляють дані попередніх вибіркових спостережень, які проводилися в аналогічних цілях.

2. Можна провести пробні обстеження на невеликому обсязі вибірки і за даними кількох таких обстежень взяти найбільше значення дисперсії або частки.

3. Невідому величину середнього квадратичного відхилення можна знайти приблизно за величиною розмаху передбачуваної варіації (К - хтах ~ хтіп). Доведено, що з імовірністю Р = 0,997 можна стверджувати, що розмах варіації в нормальному розподілі ознаки укладається в бст (крайні значення знаходяться на відстані в той або інший бік від середньої величини на 3ст), тобто ІР = бст, звідси ст = 1/6 ІР.

4. Якщо розрахунок необхідної чисельності вибірки проводиться для альтернативної ознаки і її частка невідома хоча б приблизно, то вона приймається рівною своєму максимальному значенню 0,5 і дає величину дисперсії, яка дорівнює 0,25 (рд = 0,5 o 0,5).

Тоді формули для визначення необхідної чисельності вибірки при повторному і безповторному відборі набудуть відповідно такого вигляду:

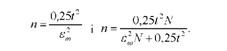
Нерідко на практиці при визначенні необхідної чисельності вибірки гранична помилка вибірки задається не абсолютною величиною. а величиною відносної помилки, яка виражається в процентах. У цьому випадку і варіація ознаки має бути виражена в процентах, тобто дисперсію ознаки замінюють на коефіцієнт варіації (V).

Чисельність вибірки для випадку, коли гранична помилка задається в процентах, визначається за такими формулами:

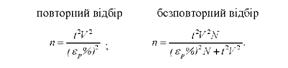
Розглянемо приклади розрахунку необхідної чисельності вибірки при повторній і безповторній вибірці.

Повторний відбір. Приклад. В TOB проектується вибіркове визначення жирності молока, що приймається від населення. Загальне поголів'я корів в особистих підсобних господарствах населення становить 180 голів. За проведеними раніше дослідженнями встановлено, що середня жирність молока становить 3,6%, а середнє коливання жирності дорівнює 0,2% (ст = 0,2%).

Потрібно визначити, яке поголів'я корів слід піддати вибірковому обстеженню, щоб визначити середню жирність молока з граничною помилкою

0,1% (% = 0.1%). Довірчий рівень імовірності Р = 0,9545, якому відповідає нормоване відхилення і = 2 (дод. 2).

При випадковому повторному відборі чисельність вибірки визначається за формулою

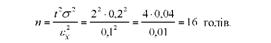
Отже, вибірковому обстеженню досить піддати 16 корів, щоб з довірчою імовірністю Р = 0,9545 (імовірність помилки в 5 випадках з 100) визначити середню жирність молока з помилкою, що не перевищує 0,1%.

Для одержання більш високої гарантії результатів вибіркового спостереження можна збільшити точність вибірки, тобто зменшити розміри припустимої граничної помилки. Так, якщо граничну помилку вибірки зменшити в два рази з 0,1 до 0,05%, то при тих самих умовах ст = 0,2% і і = 2,0 чисельність вибірки становитиме:

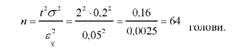
Отже, збільшення точності вибірки у два рази призводить до зростання чисельності вибірки в 4 раза (16 o 4 = 64).

Безповторний відбір.

Приклад. На свинофермі із загальним поголів'ям поросят у віці 2 - 4 місяці N = 2000 голів необхідно визначити середню живу

масу однієї голови в кінці місяця з точністю 1 кг (% = 1 кг). Довірчий рівень імовірності Р = 0,9545, якому відповідає і = 2. За даними зважування в минулому місяці (або пробному в даному) встановлено, що коливання живої маси в стаді становить 4 кг (ег= 4 кг).

Необхідно встановити, яку чисельність поросят слід відібрати для зважування, щоб середня жива маса була одержана з точністю до 1 кг. Так як зважування проводиться безповторно, то

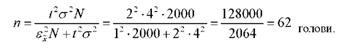
Отже, досить зважити 62 голови, щоб без великих витрат і швидко одержати відповідь із заданою, практично вірогідною точністю.