Теорія статистики - Мармоза А.Т. - 8.2. Дисперсійний аналіз при групуванні даних за однією ознакою

Порядок проведення дисперсійного аналізу при групуванні даних за однією ознакою розглянемо на такому прикладі.

В досліді вивчався вплив нових комбікормів на прирости живої маси бройлерів (табл. 8.1).

Таблиця 8.1. Середньодобові прирости живої маси бройлерів, г

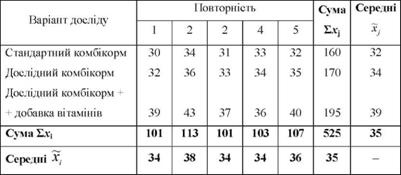
Аналіз даних таблиці показує, що середні прирости живої маси вище по групах бройлерів, що одержували дослідний комбікорм і дослідний комбікорм з добавкою вітамінів. Отже, варіація середніх по варіантах досліду зумовлювалась різним складом раціонів. Але прирости живої маси варіювали і всередині груп, тобто мала місце внутрішньогрупова (залишкова) варіація, викликана рештою неврахованих факторів. Про це свідчать середні прирости живої маси по повторностях: вони коливаються від 34 до 38 г.

На основі вихідних даних методом дисперсійного аналізу перевіримо вірогідність впливу різних за якістю раціонів на прирости живої маси бройлерів. Для цього висунемо і перевіримо статистичну гіпотезу відносно середніх в генеральних сукупностях.

Сформулюємо нульову і альтернативну гіпотези:

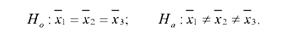
Рівень значущості приймемо рівним а = 0,05. Найпотужнішим критерієм перевірки Но є Б-критерій Фішера. Для перевірки Н0 і формулювання висновків за результатами дисперсійного аналізу необхідно обчислити фактичне значення Б-критерію Фішера і порівняти його з табличним значенням Ба.

Для розрахунку фактичного значення Б-критерію виконаємо всі необхідні операції по його обчисленню відповідно до етапів дисперсійного аналізу.

При групуванні даних за однією ознакою загальний обсяг варіації можна розкласти на варіацію, пов'язану з дією групувальної ознаки (міжгрупову або систематичну), і варіацію внутрішньогрупову (залишкову):

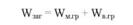
Для визначення сум квадратів відхилень піднесемо до квадрату середньодобові прирости і суми приростів (табл. 8.2).

Позначимо загальне число спостережень N = 15, число варіантів досліду т = 3, число повторностей п = 5, N = т o п = 3 o 5 = 15.

Таблиця 8.2. Квадрати середньодобових приростів живої маси

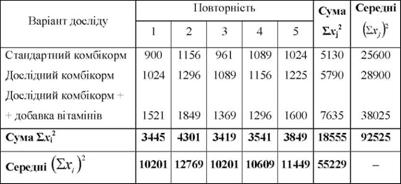
На підставі одержаних в табл. 8.2 даних обчислимо:

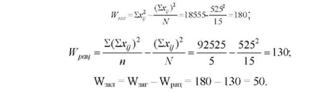
Визначення і розкладання варіації дало такі результати: ™звг = -¥рщ + -¥зал; 180 = 130 + 50 ; 100,0% = 72,2% + 27,8%. Отже, 72,2% загальної варіації середньодобових приростів бройлерів у досліді припадає на варіацію досліджуваного фактора (раціонів), а 27,8% варіації зумовлено неврахованими факторами.

Встановимо число ступенів свободи варіації для кожної суми квадратів відхилень при N = 15, т = 3, п = 5.

Тоді число ступенів свободи варіації для загальної суми квадратів відхилень

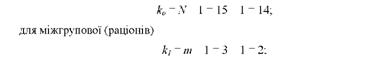
для залишкової визначається за різницею так само, як і залишкова варіація: к2 = к0 - к1 = N - 1) - (т - 1) = 14 - 2 = 12.

Знаючи суми квадратів відхилень і ступені свободи, визначимо дисперсії, як відношення суми квадратів відхилень до відповідного числа ступенів свободи варіації.

Для дисперсійного аналізу викликає інтерес міжгрупова і залишкова дисперсії, а загальна дисперсія в аналізі участі не бере, тому її не обчислюємо:

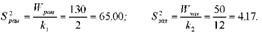
Зіставимо дисперсії, тобто знайдемо фактичне значення Б-критерію Фішера:

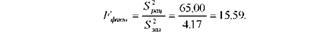
Для перевірки нульової гіпотези необхідно визначити табличне значення Б-критерію Фішера (дод. 4) і порівняти його з одержаним фактичним значенням.

V 2

Більшій дисперсії рац відповідає число ступенів свободи варіації кі =2 (чисельник відношення), меншій дисперсії зал число ступенів свободи варіації к2 = 12 (знаменник відношення). Отже, згідно дод. 4 теоретичне (табличне) значення Б-критерію знаходиться на перетині другого стовпця і дванадцятого рядка: Б005 = 3,88.

Порівняємо фактичне і табличне значення Б-критерію:

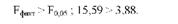
Оскільки Бфакг > Б005, висунута нульова гіпотеза щодо випадкових розбіжностей в групових середніх має бути відхилена і прийнята альтернативна гіпотеза: значення генеральних середніх істотно відрізняються. Іншими словами, фактичні дані не узгоджуються з нульовою гіпотезою. Отже, вплив різних за якістю раціонів на середньодобові прирости живої маси бройлерів вірогідний і істотний.

В дисперсійному аналізі при розкладанні загальної варіації результативної ознаки за компонентами необхідно враховувати порядок формування вибірок: залежні чи незалежні. Якщо в прикладі, що розглядується, вибірки сформовані як незалежні (тобто в кожну групу відібрано по п'ять тварин у випадковому порядку), то загальна сума квадратів відхилень поділяється на два компонента: "¥р!Щ і "¥зал. Однак частіше в дослідах з тваринами формуються групи тварин-аналогів відповідно до числа повторностей по кожному варіанту досліду. Кожен варіант досліду має за повторність - тварину-представника з групи аналогів.

При проведенні експерименту (розглянутий вище приклад) з перевірки впливу різних раціонів на прирости живої маси бройлерів могло бути сформовано п'ять груп тварин-аналогів, оскільки дослід мав проводиться у п'ятикратному повторенні. Групи складалися з трьох голів відповідно варіантам раціону і кожний варіант досліду мав представника з однієї і тієї самої групи тварин-аналогів. Отже, середні по повторностях (по графах табл. 8.1) відбивають тоді відмінності між виділеними групами. Ці відмінності необхідно виключити із загального варіювання приростів, оскільки вони не є випадковими, не пов'язані із зміною раціонів і в певній мірі можуть затушовувати вплив на прирости досліджуваного фактора.

Розкладання загальної варіації результативної ознаки при залежному формуванні вибірок ведеться за схемою:

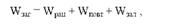
тобто на відміну від незалежного формування вибірок включає ще й варіацію повторностей.

За даними табл. 8.2 обчислимо суму квадратів відхилень повторностей:

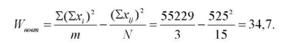
Цій сумі квадратів відхилень відповідає к"оет = п - 1 = 5 - 1 = 4 тоді дисперсія повторностей становитиме:

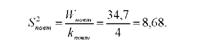
Виключення із загальної суми квадратів відхилень "¥повт призводить і до зміни "¥зал відповідних їй ступенів свободи варіації:

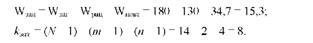
а отже, і залишкової дисперсії

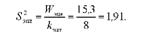
Зіставимо дисперсію раціонів і повторностей із залишковою дисперсією. Результати розрахунків оформимо в табл. 8.3.

Таблиця 8.3. Аналіз дисперсій

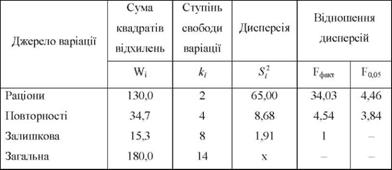
Табличне значення Б-критерію для оцінки відношення дисперсії раціонів до залишкової дисперсії знаходимо на перетині другого стовпця і восьмого рядка - Б005 = 4,46, а для відношення дисперсії повторностей до залишкової - на перетині четвертого стовпця і восьмого рядка - Б005 = 3,84 (дод. 4). Порівняння Рфакг з табличними значеннями призводить до відмови від нульової гіпотези. Отже, відмінності між середніми за раціонами і повторностями не можуть бути віднесені на рахунок випадкового варіювання.