Теорія статистики - Мармоза А.Т. - 7.6. Перевірка статистичної гіпотези про істотність розбіжностей між дисперсіями

Задача перевірки гіпотези про рівність дисперсій виникає досить часто. Наприклад, при аналізі стабільності виробничого процесу до і після впровадження нової техніки (коливання у випуску продукції вимірюється за допомогою середнього квадратичного відхилення), при вивченні ступеня однорідності двох сукупностей відносно будь-якої ознаки (стажу роботи, рівня продуктивності праці, продуктивності тварин тощо). Найчастіше необхідність перевірки гіпотези про рівність дисперсій виникає при порівнянні середніх величин сукупностей, оскільки при цьому в більшості випадків передбачається, що генеральні дисперсії рівні. Так як вибіркові дисперсії, як правило, нерівні в ході перевірки статистичної гіпотези про рівність середніх необхідно перевірити гіпотезу про істотність різниці дисперсій.

Гіпотеза про рівність дисперсій перевіряється за допомогою Г-критерію Фішера, який являє собою відношення двох вибіркових дисперсій і £22 при відповідних ступенях свободи варіації к1 і к2:

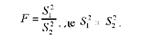
Цей критерій докладно розглядається при вивченні дисперсійного аналізу (розділ 8). Тому ми тут обмежимося лише розглядом схеми застосування критерію.

Критичне значення Га знаходиться в спеціальних таблицях (дод. 4 і 5) з урахуванням зазначених ступенів свободи при заданому рівні значущості а. Для зручності обчислень ці таблиці складені для відношень більшої дисперсії до меншої. Тому при визначенні вибіркового значення гф^ завжди більшу вибіркову дисперсію необхідно ділити на меншу. Отже, завжди г > 1.

Для перевірки нульової гіпотези про рівність дисперсій в генеральних сукупностях (ро :<?1 =а; На:а^ *<у{) слід обчислити фактичне значення г-критерію і порівняти його з табличним значенням. Оскільки дисперсії генеральних сукупностей невідомі, то перевірку висунутої гіпотези здійснюють на основі порівняння вибіркових дисперсій ?2 і . При цьому слід мати на увазі, що якщо відношення Зі2 : ?2 близьке до одиниці, то, очевидно, немає підстав для відхилення нульової гіпотези. Якщо це відношення значно відрізняється від одиниці, то даний факт може бути підставою для її відхилення.

Перевірка гіпотези Н0 зводиться до такого правила: якщо фактичне значення критерію потрапляє в область припустимих значень (гфщ^ < га) нульова гіпотеза про рівність дисперсій в генеральних сукупностях приймається; якщо ж фактичне значення критерію потрапляє в критичну область (гфакг > га), то від нульової гіпотези слід відмовитися.

Якщо альтернативна гіпотеза формулюється так: На: оі * <т2, то використовується двосторонній критерій. Якщо ж відомо, що одна з дисперсій передбачувано більше другої, то альтернативна гіпотеза На :оІ >ег2 і використовується односторонній критерій.

Порядок перевірки гіпотези про істотність різниці між дисперсіями розглянемо на такому прикладі. Нехай, шляхом направленого відбору з місцевого стада овець виведена нова лінія, що характеризується більшою плодючістю на одну матку. Для короткості вихідну сукупність назвемо групою І, а нову лінію групою ii.

Припустимо, встановлено, що дисперсія в групі ii менша (група більш однорідна).

Для перевірки істотності різниці дисперсій відібрано таку кількість тварин:

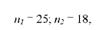
при цьому = 12,8; 8^ = 4,6.

Сформулюємо нульову і альтернативну гіпотези:

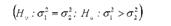
Рівень значущості приймемо рівним а = 0,05. Визначимо фактичне значення Г-критерію:

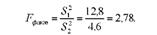
Табличне значення Г-критерію при к1 = п1 - 1 = 25 - 1 = 24 і к2 = п2 --1 = 18 - 1 = 17 і а = 0,05 становить Гад5 = 2,19 (дод. 4).

Оскільки Гфщ^ > Г005; 2,78 > 2,19 нульова гіпотеза про рівність дисперсій відхиляється. Це означає, що дисперсія ознаки в II групі суттєво нижче.

Для великих вибірок перевірка гіпотези про рівність дисперсій може бути проведена на основі Г-критерію нормального розподілу:

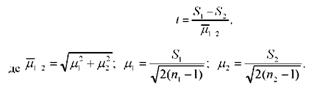
Тут ми розглянули лише випадок перевірки гіпотези про рівність двох дисперсій. Якщо ж потрібна оцінка істотності відмінностей ряду дисперсій, то застосовуються інші критерії:

а) критерій Кохрана, якщо чисельності вибірок рівні;

б) критерій Бартлетта, якщо чисельності вибірок нерівні.