Для розробки виробничих програм поточного і перспективного фінансового планування діяльності підприємств необхідною умовою їхнього функціонування є врахування різних факторів (умов), таких як режим роботи підприємства, вид залежності витрат від обсягів випуску продукції, узгодженість в роботі окремих структурних підрозділів і т. д. З метою наочності та загальності викладення процедур коригування суперечливої системи обмежень даний підхід до подолання несумісності в задачах перспективного і поточного фінансового планування подається на прикладі найпростіших моделей задач фінансового планування виробничо-господарської діяльності.
6.4.2.1. Класифікація невласних задач лінійного та випуклого програмування
Запишемо задачу лінійного програмування:
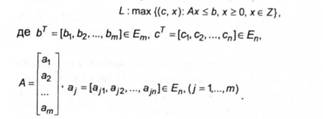
Тут ї- множина цілих чисел. Нехай 7-ї' оптимальне значення.
Форма запису (6.1) задачі і зручна через її стандартну виробничо-економічну інтерпретацію, відповідно до якої Ь -- вектор ресурсів, с - вектор цін. Стовпці матриці А моделюють технологічні способи шляхом завдання витрат ресурсів, які припадають на одиничну інтенсивність використання відповідних способів, так що вектор інтенсивності х= [х,, х2,..., ху задає рівень виробництва (фінансовий план виробництва).
Двоїстою до (6.1) виступає задача лінійного програмування
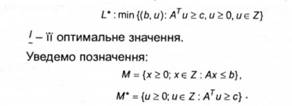
Ці множини називаються допустимими для /_ і і* відповідно.
Основний факт, що пов'язує задачі і і £.*, формулюється як теорема двоїстості: якщо задача /. розв'язувана, то /_* також розв'язувана, при цьому їхні оптимальні значення збігаються: / = / .
Якщо задача і розв'язувана, то вона називається власною задачею, якщо ж ні - невласною.
Припущення М* 0, М" * 0 рівносильне розв'язуваності задачі і, а відповідно, і задачі і*.
Якщо задача і невласна, то можливі такі три випадки:
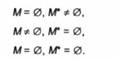
Залежно від того, чи виконується одна з умов (6.3) - (6.5), будемо говорити про невласну задачу і відповідно 1-го, 2-го та 3-го роду.
З даної класифікації невласних задач лінійного програмування видно, що коли і - невласна задача 1-го роду, то і* - 2-го роду (і навпаки); якщо і - невласна задача 3-го роду, то /.* - також невласна задача 3-го роду (і навпаки).
Розглянемо кожну з цих умов. Перша з них означає, що, як тільки за деякого прирощення ДЬ є Ет система нерівностей
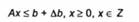
сумісна, то задача
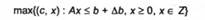
розв'язувана.
Дійсно, із сумісності системи (6.6) та умови М*ф0 виходить розв'язуваність (6.7), а відповідно, в силу теореми двоїстості і
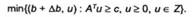
А також, якщо при деякому АЬ задача (6.7) розв'язувана, то, розв'язувана і задача (6.8), то М* ф 0.
Умова (6.4) означає, що в задачі і оптимальне значення 7 дорівнює + оо. а умова (6.5) еквівалентна тому, що при будь-якому прирощенні АЬ, яке забезпечує розв'язуваність системи (6.6), оптимальне значення задачі (6.7) дорівнює + оо, що є наслідком теореми двоїстості для задач лінійного програмування.
Запишемо задачу випуклого програмування у формі
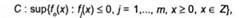
де 2- множина цілих чисел.
Введемо позначення: 7 - оптимальне значення задачі (6.9),
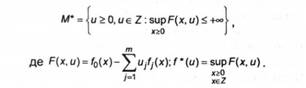
Двоїстою до С будемо вважати задачу
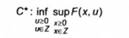
або еквівалентну до неї задачу
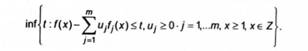
Остання має вигляд задачі лінійного програмування з нескінченним числом обмежень. Задача (6.9) називається власною, якщо
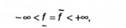
де І - оптимальне значення задачі (6.10); в іншому випадку -невласною.
Виділимо (як у лінійному випадку) три класи невласних задач випуклого програмування залежно від пустоти або непусто" ти допустимих множин М і ЛГ задач С і С* відповідно:
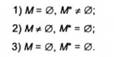
Залежно від виконуваності властивостей (6.1)-(6.3) будемо говорити про невласну задачу С 1-го, 2-го або 3-го роду відповідно.
Для невласних задач випуклого програмування не може бути дано характеристику у тій формі, яка має місце для невласних задач лінійного програмування. Проте справедливі формули
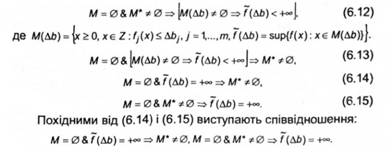
6.4.2.2. Змістовна інтерпретація невласних задач лінійного програмування
6.4.2.3. Моделі коригування невласних задач
6.5. Основні фінансові елементи в системі бізнес-планування
Глава 7. КАТЕГОРІЇ РИЗИКУ І ЛЕВЕРИДЖУ
7.1. Леверидж та його роль у фінансовому менеджменті
7.2. Методика розрахунку критичного обсягу продажів
7.3. Оцінка виробничого левериджу
7.4. Оцінка фінансового левериджу
РОЗДІЛ 3. УПРАВЛІННЯ АКТИВАМИ ПІДПРИЄМСТВА: ФІНАНСОВІ РІШЕННЯ