Економічна теорія управління фірмою - Іванова Н.Ю - Кількісний аналіз попиту

Завданням аналізу попиту є встановлення зв'язків між різними факторами, що впливають на процес реалізації товару, і попитом на цей товар. Одним з найбільш поширених методів кількісного аналізу попиту є кореляційно - регресійний (статистичний) аналіз.

За допомогою кореляційного аналізу можна з'ясувати наявність зв'язків між факторами з тим, щоб залишити у моделі ті фактори, які:

- мають найбільш істотний вплив на залежний фактор;

- є максимально незалежними між собою. Завдання регресійного аналізу полягає у побудові регресійної

моделі, яка описує форму зв'язку між залежним фактором і незалежними факторами.

Крім того, що за допомогою кореляційно-регресійного аналізу можна побудувати функцію попиту, його результати мають достатньо широкий спектр практичного використання. Основними напрямками такого використання є:

1. При побудові оптимальної економіко-математичної моделі залежний фактор доцільно вводити у цільову функцію, а незалежні - у обмеження.

2. Регресійна модель використовується для планування діяльності фірми. Вона надає можливість приймати рішення якщо і не в умовах визначеності, то хоча б в умовах ризику. Однак важливо пам'ятати, що прогнозування доцільне лише за умов збереження тенденцій, що склалися.

3. Коефіцієнти при параметрах регресійної моделі використовуються для оцінки еластичності залежної змінної за незалежними змінними.

В загальному випадку попит на товар залежить не лише від ціни на нього, а й від інших факторів. Визначити форму і тісноту зв'язку між попитом і двома чи більше факторами можна за допомогою множинного кореляційно-регресійного аналізу. Основою цього аналізу є оцінка параметрів регресії (коефіцієнтів) для кожної незалежної змінної. Кожен параметр (коефіцієнт) є мірою того, як кожна незалежна змінна впливає на залежну змінну за умов, що всі інші незалежні змінні залишаються сталими.

Багато функцій попиту є практично лінійними і мають такий загальний вигляд:

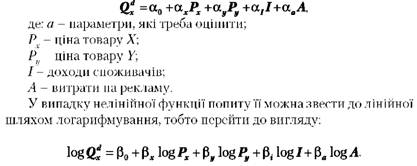
Побудова регресійної моделі здійснюється за допомогою відповідних комп'ютерних програм, які також здійснюють розрахунки статистичних тестів. Однак комп'ютер лише виконує розрахунки, що закладені у програмі. Завдання менеджера полягає в тому, щоб визначити придатність моделі для використання.

Придатність моделі визначають шляхом відповіді на такі запитання:

Чи мають параметри регресії правильний знак і розумні значення?

Наскільки якісно зміни попиту пояснюються змінами незалежних змінних (як в сукупності, так і окремо за кожною змінною). Чи мають незалежні змінні статистичну значущість?

Крок 1 (тестування придатності моделі)

а) знаки коефіцієнтів

Кожен коефіцієнт регресії - це граничне значення реакції змінної попиту на одиничну зміну відповідної незалежної змінної.

Знак параметра перевіряється для того, щоб визначити, чи показує він теоретично правильну зміну змінних.

Якщо знак неправильний, то:

- або модель побудована неправильно;

- або існує мультиколінеарність.

б) величини коефіцієнтів

Це перевірка параметра на економічний зміст. Іноді параметр може мати таке значення, яке не має економічного сенсу. Особливо це важливо, коли рівняння регресії у натуральному вигляді. Наприклад:

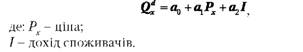
Нехай знаки параметрів правильні, але a₂= 1,3. Це означає, що з кожного додаткового долара доходу споживач має витратити 1,3 долара на купівлю. Однак це - безглуздя.

Крок 2 (статистичні тести й оцінки) а) дані тестів (для регресії в цілому)

Для регресії в цілому існують такі тести:

- множинний коефіцієнт детермінації, R²;

- скоригований коефіцієнт детермінації, R²;

- статистика для регресії;

- середня квадратична похибка для регресії;

R² (множинний коефіцієнт детермінації) - міра того, наскільки лінія регресії співпадає із експериментальними даними. R² показує, на скільки відсотків зміна залежної змінної пояснюється змінами всіх незалежних змінних і знаходиться в межах:

0 < R² < 1.

Показник має суто математичний зміст і може бути близьким до 1 лише тому, що кількість спостережень менше кількості оцінюваних параметрів. Якщо R² = 1, то кількість спостережень дорівнює кількості незалежних параметрів. Це свідчить про недостатність інформації. Тому використовують R².

Зазвичай, якщо кількість спостережень перевищує кількість незалежних параметрів хоча б у 5 або 4 рази, то прийнятним вважається

R² > 0,75.

Коефіцієнти R² і R² показують величину варіації, яку можна пояснити. Однак вони не говорять про статистичну значущість цієї варіації. Для цього використовують ^-статистику.

Чим вище - статистика, тим краще лінія регресії відповідає вихідним даним.

Для оцінки статистичної значущості F використовують таблиці критичних значень F-розподілу. Таблиці з рівнем значущості 0,05 відповідають рівням довіри 95%. Якщо розраховане значення Б перевищує відповідне критичне значення, то це означає, що ми на 95% можемо бути впевнені в тому, що істинне значення параметрів регресії не дорівнює 0.

Однак це не означає, що всі незалежні змінні значущі. Кожна незалежна змінна має бути перевірена на статистичну значущість.

Середня квадратична похибка S_е характеризує розкид спостережень від теоретичної регресії.

Чим менше S, тим сильніший зв'язок між залежною і незалежними змінними і тим краще лінія регресії описує вихідні дані. б) дані тестів (для окремих параметрів).

Для параметрів окремих змінних найчастіше використовуються такі тести:

- середня квадратична похибка коефіцієнта регресії (SERC);

- t -статистика;

- Р (імовірність).

Середня квадратична похибка коефіцієнта регресії (SERC) визначає розкид значень відносно коефіцієнта регресії. Якщо SERC має невелике значення відносно до параметра, який оцінюється, то це означає, що параметр наближається до істинного значення.

Якщо окрема незалежна змінна є статистично значущою, то істинне значення її параметра не дорівнює нулю. Це припущення перевіряється за допомогою t-статистики.

Практичне правило для використання t-статистики говорить, що коли абсолютне значення t-статистики більше 2, то можна з 95% впевненістю вважати, що істинне значення параметру не є 0 (тобто отримана оцінка параметра близька до його істинного значення).

Більш точним показником статистичної достовірності є Р. Чим менше Р, тим більш достовірна отримана оцінка, зазвичай, якщо Р < 0,05, то вважають, що оцінюваний коефіцієнт є статистично достовірним.

Як вже зазначалося, коефіцієнти при параметрах регресійної моделі є відповідними коефіцієнтами еластичності попиту. Так, для лінійної функції попиту

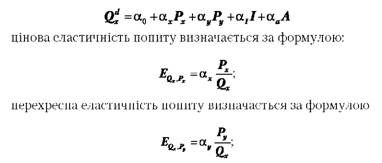
еластичність попиту за доходом визначається як

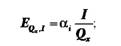
еластичність попиту за витратами на рекламу визначається таким чином

А

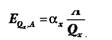
Для логарифмічної функції