Економічний аналіз - Мних Є.В. - 2.6. Застосування економіко-математичних методів і моделей у розв'язку аналітичних задач

Ускладнення об'єктів аналітичного дослідження і функцій управління вимагає широкого використання сучасних методів розв'язання економічних задач із застосуванням математики та кібернетики. Теорія і практика економічного аналізу охоплюють понад сто різних видів економіко-математичних методів і моделей, які умовно можна класифікувати за групами:

• методи кореляційно-регресійного аналізу;

• методи математичного програмування;

• матричні методи та моделі;

• інші економіко-математичні методи і моделі.

Методи кореляційно-регресійного зв'язку в економічному аналізі використовують для виявлення форми та щільності зв'язку між різними параметрами досліджуваного об'єкта, характер функціональної залежності між якими невизначено.

Найчастіше цей зв'язок є стохастичним. Кореляція виражає ймовірнісну залежність між змінними параметрами алгоритму зв'язку. Кореляційна залежність може бути виявлена як між двома кількісними ознаками (парна кореляція), так і між багатьма (множинна кореляція).

Основне завдання кореляційно-регресійного аналізу — забезпечити репрезентативність даних, обґрунтованість застосування до досліджуваного явища відповідних імовірнісних схем, що практично зводиться до вибору рівняння відповідної кривої (параболи чи гіперболи) та ін. Отже, на першому етапі визначають показники-фактори кореляційного зв'язку, які достатньо корельовані у зміні досліджуваного показника. Визначивши вид рівняння, методом найменших квадратів розраховують його параметри за вихідними даними. На другому етапі визначають щільність зв'язку результативного показника з показниками-факторами, яка виражається коефіцієнтами парної чи множинної кореляції. Значення коефіцієнтів показує, яка ймовірність зміни результативного показника, якщо показник-фактор змінити на один пункт.

Залежність досліджуваного показника від одного фактора у найбільш спрощеному вигляді можна виразити таким алгоритмом:

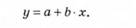
Для визначення параметрів аіЬ використовують метод найменших квадратів, який полягає у розв'язанні системи рівнянь:

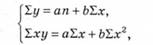
де п — кількість спостережень; у — результативний показник; х — факторний показник; а і Ь — сталі значення.

Коефіцієнт парної кореляції (кху) визначають за формулою

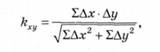
де Ах — відхилення від середньої ряду значень показника х; Ау — відхилення від середньої ряду значень показника у. Складніші залежності можуть бути виражені рівнянням множинної лінійної кореляції

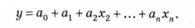
Коефіцієнт множинної кореляції (М) визначається так:

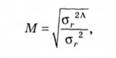
де аг2Л — дисперсія значень величини і/, при підстановці взятих зі спостережень значень факторів х у знайдене рівняння

регресії У =/(*і, *2" *8" •••• *п)>

ог2 — дисперсія фактичних значень величини у.

Рівняння регресії визначають та розв'язують, використовуючи спеціальні програми для ЕОМ. Аналітик повинен формувати задачу аналітичного дослідження та правильно інтерпретувати її розв'язки. Якщо аналітик логічно може досить ефективно оцінити значущість розв'язку, то побудова рівняння регресії значно спрощується.

На базі методів кореляційно-регресійного зв'язку сформовано економіко-математичний метод аналізу — метод виробничої функції.

Методи математичного програмування призначені для оптимізації господарської діяльності. Цінність їх полягає у тому, що вони дають змогу оцінювати ступінь досягнення потенціалу, визначати лімітуючі ресурси, "вузькі місця", ступінь конкурентності та дефіцитності.

Методи математичного програмування охоплюють методи лінійного та динамічного програмування.

Методи лінійного програмування (транспортна задача, задача оптимального розкрою, задача оптимальної суміші та ін.) використовують для розв'язання багатьох оптимізаційних аналітичних задач, де функціональні залежності досліджуваних явищ і процесів детерміновані.

У задачах лінійного програмування повинні виконуватись три основні умови.

Умова 1. Обмеженість ресурсів:

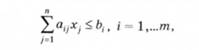
де а — норматив витрати і'-го ресурсу на зміну у-го параметра досліджуваного об'єкта;

х— значення у-го параметра досліджуваного об'єкта;

Ь — ліміт і-то ресурсу.

Умова 2. Невід'ємність зміни значень у-го параметра досліджуваного об'єкта:

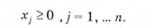
Умова 3. Критерій оптимізації зміни досліджуваного об'єкта:

л

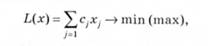
де с. — кількісна оцінка значущості зміни у-го параметра на один пункт.

Досягнення основних аналітичних результатів при застосуванні методів лінійного програмування виявляються у визначенні потенціальних можливостей зміни будь-якого параметра досліджуваного об'єкта, а також резервів нереалізованих можливостей. Задачі лінійного програмування успішно розв'язують на базі створеного програмного забезпечення роботи ЕОМ.

Методи динамічного програмування використовують для розв'язання оптимізаційних задач, у яких цільова функція або обмеження характеризуються нелінійними залежностями. Ці методи використовують під час дослідження стохастичних факторних систем. Задачі динамічного програмування розв'язують шляхом поетапного розв'язання певної кількості оптимізаційних задач, диференційованих за лінійними формами. Як і у випадку розв'язання задач лінійного програмування, використовують спеціальне програмне забезпечення роботи ЕОМ.

Матричні методи та моделі економічного аналізу ґрунтуються на лінійній і векторно-матричній алгебрі, їх використовують при дослідженні складних і великорозмірних економічних структур. Найпоширенішими в аналізі є матрична модель міжгалузевого балансу, матриця багатокритеріальної оптимізації, ключова матриця та ін.

Модель міжгалузевого балансу є важливим методом економічного аналізу складних пропорційних залежностей, коли за кількістю виміряних прямих зв'язків визначається вся сукупність зв'язків (прямих і непрямих). Наприклад, продуктова матрична модель міжгалузевого балансу має такий вигляд:

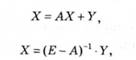
де X — матриця сукупного виробництва продукції;

У — матриця сукупного кінцевого споживання продукції;

А — матриця прямих витрат ресурсів на виробництво продукції;

Е — одинична матриця.

Для будь-якого і-го продукту буде виділене рівняння типу:

В економічному аналізі модель міжгалузевого балансу використовують для розрахунку технологічних нормативів, внутрішньогосподарських виробничо-технологічних розрахунків, аналізу збалансованості виробництва, калькулювання собівартості продукції тощо. Розв'язують задачі типу міжгалузевого балансу з використанням спеціального програмного забезпечення ЕОМ.

Матрицю багатокритеріальної оптимізації використовують в економічному аналізі як метод порівняльної, рейтингової оцінки варіантів можливих змін параметрів економічної системи на багатокритеріальній основі. За формою це одинична матриця з виокремленням у ній заданої кількості критеріїв порівняння (табл. 2.9).

Матриця може бути збільшена залежно від кількості введених критеріальних ознак. Наприклад, мінімум витрат можливий за відсутності обмежень на використання певних видів сировини, максимальний випуск — за різних обмежень асорти-

Таблиця 2.9. Матриця багатокритеріальної оптимізації діяльності підприємства

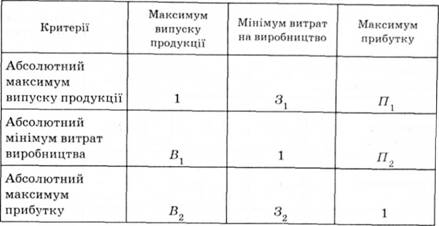
менту товарів. За пріоритетними критеріями може бути проведений рейтинг оптимальних результатів, наприклад, за значенням прибутку на 1 грн витрат.

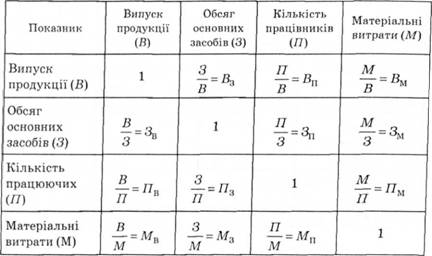
Метод ключової матриці дає змогу спростити розв'язання задач методом виробничих функцій. Він полягає у тому, що вся система функціональних зв'язків (детермінованих і стохастичних) у досліджуваному об'єкті аналізу максимально агрегується до утворення детермінованих факторних систем. Алгоритм факторної системи будують за участю коефіцієнтів міжелементного зв'язку, а деякі з них не мають чіткої економічної інтерпретації (наприклад витрата сировини в розрахунку на одного робітника за зміну) (табл. 2.10).

У складі інших економіко-математичних методів і моделей можна виокремити математичну теорію гри, математичну теорію масового обслуговування, теорію нечітких множин.

Математичну теорію гри використовують тоді, коли обирають найвигідніші управлінські рішення, при організації статистичного спостереження і контролю, при організації господарських взаємовідносин з партнерами та в інших ситуаціях. В управлінні ця теорія набула форми ділової гри. Сформулювавши конфліктні ситуації, математично їх можна подати як гру двох, трьох чи більше партнерів, кожен з яких хоче

Таблиця 2.10. Модель ключової матриці базових показників виробничо-господарської діяльності підприємства

максимізувати свою вигоду за рахунок іншого партнера. Розв'язуючи такі задачі визначають умови гри: кількість партнерів і правила гри, можливі стратегії партнерів, можливе отримання вигоди. Важливою є сукупність правил гри, за якими залежно від ситуації вибір партнера буде однозначним. Кількість стратегій може бути скінченною і нескінченною. Дослідження стратегій ґрунтується на використанні математичного апарату (лінійних рівнянь і нерівностей, ітераційних методів тощо). Якщо виграш одного партнера дорівнює програшу іншого, то їх алгебрична сума дорівнює нулю. Ці ігри називають нульовими. Кожній стратегії відповідає певний виграш (+), або програш (-), залежно від обраної супротивником стратегії. Відповідну інформацію можна подати у вигляді матриці. Наприклад, у парній грі (табл. 2.11) умови гри містять можливі стратегії кожного партнера і суми виграшу чи програшу для будь-якого поєднання стратегій. Партнер А має три, а партнер Б — чотири стратегії. У табл. 2.10 наведено тільки суми виграшу гравця А, бо для гравця Б ця сама сума буде програшем. Які ж стратегії краще обирати партнерам? Партнер А користуючись стратегією А,, може виграти 10 одиниць, стратегією А2 — 9, а стратегією А3 —11. Але за теорією гри треба вважати, що другий партнер обиратиме стратегії, які дадуть партнерові А не найбільший, а найменший виграш. Такими за стратегії А1 є 3 одиниці, за А2 — 5 і за А3 — 1 одиниця.

Таблиця 2.11. Умови гри

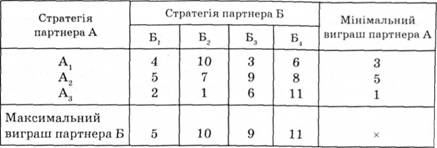
Якщо врахувати, що партнер А дуже обережний, то на максимальні виграші він не орієнтується. Він думає так: якщо я оберу стратегію А2, то гарантуватиму собі виграш не менше 5 одиниць, а за інших стратегій він може бути меншим. Саме ця стратегія партнера А і буде оптимальною. Партнер Б за будь-якої стратегії буде у програші, але програвати він намагатиметься якомога менше. Такою стратегією є Б., обравши яку більше 5 одиниць він не програє. Він і обирає цей мінімакс. Отже, партнер А орієнтується на максимін, а партнер Б — на мінімакс. У цій грі їхня тактика збігається, і такий збіг називають сідловою точкою, значення якої визначає ціну гри.

У теорії гри розглядають і складніші задачі, які виникають внаслідок збігу суми виграшу та програшу, за виникнення домовленостей (кооперативні ігри), за непостійної кількості учасників гри, за гри з випадковим результатом та ін.

Математичну теорію масового обслуговування використовують при розв'язанні соціально-економічних задач, пов'язаних з організацією обслуговування та ремонту устаткування, проектуванням потокових ліній, плануванням маршрутів міського транспорту, організацією телефонної служби тощо. Завдання теорії масового обслуговування — визначити такі характеристики системи, які забезпечують задану якість її функціонування. Основними елементами системи масового обслуговування, які характеризують структуру, склад і функціональні зв'язки, є вхідний потік запитів, послідовність запитів і засоби обслуговування.

За строком перебування запитів у системі до початку обслуговування системи масового обслуговування поділяють на три групи: з необмеженим часом очікування, з відмовами (втратами) і змішаного типу. У першій еру пі, якщо всі засоби обслуговування зайняті, елемент системи, що надійшов, чекає доти, доки один з них не звільниться. У системах з відмовами будь-який елемент, що надійшов, а усі засоби зайняті, виходить із системи. У системах змішаного типу елемент, надійшовши до системи, де усі засоби зайняті, перебуває у ній обмежений час, протягом якого або буде обслужений, або залишить систему. Прикладом такої системи є телефонна станція.

До завдань теорії масового обслуговування належать:

• пошук залежностей, які характеризують якість функціонування обслуговування залежно від характеристик вхідного потоку;

• пошук параметрів, які характеризують можливості обслуговування;

• вибір способу організації системи загалом.

Задачі теорії масового обслуговування можна розв'язати, використовуючи широку мережу потужних ЕОМ. У випадку, коли система масового обслуговування дуже складна і її треба розв'язати без спрощень, використовують певний імітаційний метод, що потребує значних витрат машинного часу.

Метод дослідження операцій використовують в аналізі для отримання порівняльної оцінки альтернативних рішень. Він має на меті об'єктивно оцінити пропоновані цілеспрямовані дії і, можливо, запропонувати альтернативні варіанти. Складність методу полягає у тому, що досліджувані цілеспрямовані дії (операції), не ізольовані, а пов'язані з іншими діями, які дослідника у цей час не цікавлять, однак можуть впливати на хід операції. Усвідомлення операції, її мети, аналіз факторів, які стосуються цієї мети, порівняння витрат і результатів повинні дати аналітику підставу виокремити найважливіше і сформулювати умови задачі, провівши добір показників.

Вибором показників і їх формалізацією, визначенням допустимої області зміни та побудовою цільової функції починається другий етап дослідження операцій — перехід від описової до формальної моделі.

Надалі здійснюється аналіз моделі переважно шляхом статистичного моделювання, за допомогою експертних оцінок, ділових ігрових імітацій тощо.