Обгрунтування господарських рішень та оцінювання ризиків - Донець Л.І. - 3.5.4. Критерій мінімаксного ризику Севіджа

У випадку, коли ОПР орієнтується на найменш сприятливі умови та неконтрольовані фактори застосовують критерій песимізму.

Для гри, яку задано матрицею виграшів за критерієм песимізму визначається варіант рішення, який мінімізує мінімальні виграші для кожного варіанта ситуації. Критерій песимізму записують у вигляді

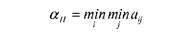
Для гри, яку задано матрицею програшів за критерієм песимізму визначається варіант рішення, який максимізує максимальні програші для кожного варіанта ситуації. Критерій песимізму записують у вигляді

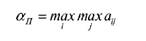
За критерієм песимізму передбачається, що неконтрольовані фактори можуть бути використані несприятливим чином. В реальних ситуаціях можуть в багатьох задачах неможливий контроль за неконтрольованими факторами. Це відноситься до задач, в яких є необхідність урахування фактору часу; задач соціально-економічного прогнозування; задач довгострокового планування тощо.

Наприклад, витрати виробництва є контрольованими факторами на короткострокових часових інтервалах, але при аналізі довгострокових проектів певні елементи витрат виробництва стають неконтрольованими: вартість електроенергії, вартість матеріалів тощо.

Приклад 3.5. Для гри, яку задано матрицею виграшів у прикладі 3.2, за критерієм оптимізму вибрати стратегію, яка є найбільш вигідною.

Розв'язання. Запишемо матрицю виграшів у вигляді таблиці 3.6 і знайдемо найменше значення minaij для кожного рядка.

Таблиця 3.6

Матриця виграшів гри

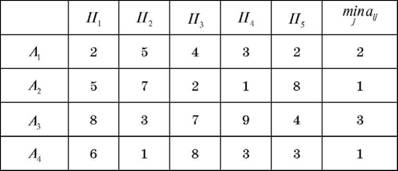
За формулою (3.16) маємо:

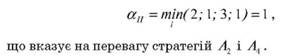
Це означає, що незалежно від того яку стратегію буде застосовувати гравець "природа", тобто який зі станів складеться на ринку, гравець А (статистик), при застосуванні стратегій А2 і А4, тобто техніки видів А2 і А4, отримає гарантований виграш не менше 1 одиниці. При використанні гравцем А будь-якої іншої стратегії, тобто випуску іншого виду техніки, у випадку гіршої ситуації може бути отриманий виграш менший ніж 1 одиниця.

3.5.4. Критерій мінімаксного ризику Севіджа

Виникають ситуації, в яких неконтрольовані фактори діють більш приємним чином у порівнянні з найкращім становищем, на яке орієнтувалась ОПР. Наприклад, погодні умови оказалися краще прогнозованих; конкуренція зменшилась на ринку у порівнянні з прогнозованими очікуваннями. У цих умовах виникає необхідність визначення можливих відхилень отриманих результатів від їх оптимальних значень. У цьому випадку застосовують критерій Севіджа.

Цей критерій аналогічний попередньому критерію Вальда, але ОПР використовує не матрицю виграшів А, а матрицю ризиків Я .

За критерієм Севіджа кращим є рішення, при якому максимальне значення ризику буде найменшим, тобто

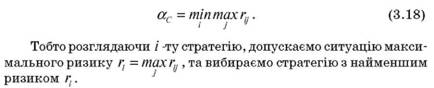
Для застосування критерію Севіджа до ситуації пред'являються ті ж самі умови, що й для критерію Вальда.

Приклад 3.6. Для вихідних даних прикладу 3.2 за критерієм Севіджа вибрати стратегію, яка є найбільш вигідною.

Розв язання. Запишемо матрицю ризиків гри у вигляді таблиці 3.7 і знайдемо найбільше значення max rij для кожного рядка.

Таблиця 3.7

Матриця ризиків гри

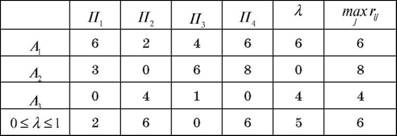
тобто вибираємо стратегію А3 , при застосуванні якої статистиком величина ризику, що дорівнює 4 одиниці, приймає мінімальне значення у самій гіршій ситуації.

Помітимо, що цей вибір оптимальної стратегії збігається з вибором за критеріями Вальда і оптимізму.

Суть критерію Севіджа полягає у прагненні уникнути великого ризику при виборі рішення (стратегії).

3.5.5. Критерій песимізму-оптимізму Гурвіца

Цей критерій рекомендує в процесі прийняття рішення використовувати певний середній результат, що характеризує стан між крайнім песимізмом і крайнім оптимізмом.

У випадку, коли гру задано матрицею виграшів за критерієм Гурвіца перевага віддається варіанту рішення, яке визначається максимумом серед лінійних комбінацій мінімального і максимального виграшів:

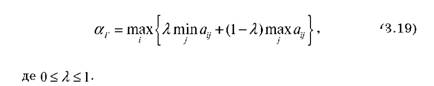
Коефіцієнт λ можна розглядати як показник оптимізму.

При λ = 0 критерій Гурвіца співпадає з максимаксним критерієм, тобто орієнтація на граничний ризик, оскільки великий виграш спрягається з великим ризиком. При λ = 1 критерій Гур-віца співпадає з критерієм Вальда, тобто орієнтація на обережну поведінку. Тому критерій Гурвіца це називають критерієм узагальненого максиміну.

Значення λ є проміжними між ризиком і обережністью і вибирається із суб'єктивних (інтуїтивних) міркувань в залежності від конкретних умов та схильності до ризику ОПР.

У випадку, коли гру задано матрицею програшів за критерієм Гурвіца перевага віддається варіанту рішення, яке визначається мінімумом серед лінійних комбінацій мінімального і максимального виграшів:

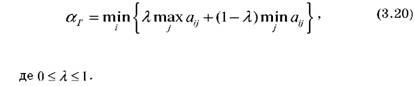
Формулу (3.20) застосовують також у випадку, коли задано матрицю ризиків.

Критерій Гурвіца застосовується у випадку, коли:

про ймовірність появи стану Пj нічого не відомо;

з появою стану Пj необхідно вважатися; реалізується тільки мала кількість рішень; допускається деякий ризик.

Приклад 3.7. Для гри, яку задано матрицею виграшів у прикладі 3.2, за критерієм Гурвіца при λ = 0,6 вибрати стратегію, яка є найбільш вигідною.

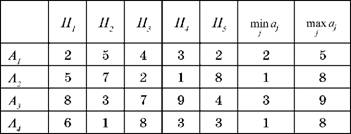
Розв'язання. Запишемо матрицю виграшів у вигляді 1 таблиці 3.8 і знайдемо найменше значення min аj, і найбільше значення max аj, для кожного її рядка.

Таблиця 3.8. Матриця виграшів гри

Визначимо максимум серед лінійних комбінацій мінімального і максимального виграшів за формулою (3.19):

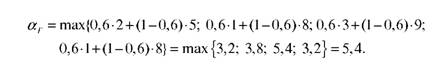
Таким чином, за критерієм Гурвіца при значенні показнику оптимізму λ = 0,6 слід вибрати стратегію А3.

Помітимо, що цей вибір оптимальної стратегії збігається з вибором за критеріями Вальда, оптимізму і Севіджа.