Обгрунтування господарських рішень та оцінювання ризиків - Донець Л.І. - 5.3.5. Статистичні розподіли втрат

Одна з важливих задач аналізу варіаційних рядів - послідовності варіант, взятих з генеральної сукупності певної досліджуваної ознаки Х, зокрема втрат - полягає у виявлені закономірності розподілу і визначені її характеру. З цією метою будують варіаційні ряди достатньо великих сукупностей. Велике значення для виявлення закономірностей розподілу має правильна побудова варіаційного ряду: вибір числа груп і розміру інтервалу ознаки, що варіюється.

Якщо розподіл проведено за дискретної ознакою, що виражена цілими числами, то такий варіаційний ряд називають дискретним; якщо розподіл проведено за кількісною ознакою, що виражена у вигляді інтервалів, то маємо інтервальний варіаційний ряд. Складовими елементами варіаційного ряду є ряд варіант (окремі числові значення ознаки, що варіюється) і ряд частот (числа, які показують кількість разів зустрічається кожна варіанта).

Якщо ми говоримо про характер, тип закономірності розподілу, то маємо на увазі відображення в ньому загальних умов, що визначають варіацію. При цьому мова йдеться завжди про розподіли якісно однорідних явищ. Загальні умови, що визначають тип закономірності, пізнаються аналізом сутності явища, тих його властивостей, що визначають варіацію ознаки, що вивчається. Тобто необхідно висунути наукову гіпотезу, що пояснює певний тип теоретичної кривої розподілу.

Під теоретичною кривої розподілу розуміють графічне зображення ряду у вигляді неперервної лінії зміни частот у варіаційному ряді, який функціонально зв'язаний зі зміню варіант (значень ознаки). Теоретичний розподіл може бути виражено аналітичне - формулою, що зв'язує частоти варіаційного ряду і відповідні значення ознаки. Такі формули називають законами розподілу.

Випадкова величина - це змінна величина, конкретне значення якої не визначене, залежить від випадку, але для якої визначена функція розподілу ймовірностей. Остання й дозволяє аналізувати ступінь ризику.

В умовах обмеженої інформації буває важко обрати емпіричну функцію розподілу ймовірностей. Тому в практичних розрахунках, мабуть, зручніше користуватися найчастіше уживаними в теорії ймовірностей стандартними функціями розподілу ймовірностей, зокрема: нормальним розподілом ймовірностей, розподілом Гаусса, показниковим (експоненційним) розподілом, розподілом Пуассона. Практика розрахунків може показати й інші, зокрема емпіричні, розподіли ймовірностей.

Типовим графіком розподілу ймовірностей втрат, що характеризують ступінь підприємницького ризику, можна вважати криву нормального розподілу.

У канонічному виді нормальний розподіл випадкової величини записується щільність розподілу ймовірностей втрат Х за формулою (5.11) (рис. 5.6).

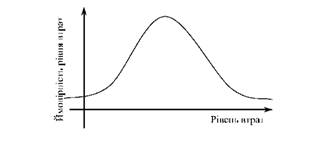
Рисунок 5.6 - Нормальний розподіл рівня втрат

Інтегральна функція нормального розподілу визначається таким чином:

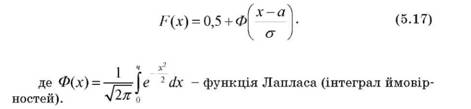
Вибір функції нормального розподілу (5.11) можливо обґрунтувати такими припущеннями:

ймовірність відсутності збитків практично дорівнює нулю, тому що при здійсненні заходу якісь втрати будуть, а у разі відмови від здійснення заходу його ймовірність дорівнює нулю;

ймовірність надзвичайно великих збитків також можна розглядати як таку, що дорівнює нулю, бо в практичній діяльності втрати завжди мають межу;

між мінімальними (нульовими) й максимальними збитками існує деякий рівень збитків, що очікується як найбільш ймовірний. Щільність ймовірностей у цій області збільшується;

нарешті, резонно припустити, що крива ймовірностей втрат змінюється неперевно і монотонно, зростаючи від нуля до найбільшого значення ймовірності і спадаючи від найбільшого значення до нуля у разі збільшення втрат від нуля до максимуму.

Звичайно, важко припустити, що графік розподілу ймовірностей втрат обов'язково буде мати вигляд класичної кривої нормального розподілу. Він може бути асиметричним, мати ексцес тощо, але для аналізу цих зміщень потрібно мати достатньо інформації або вагомі аргументи для обґрунтування напрямів таких зміщень.

Ризик підприємства на ринку вільної конкуренції у разі відхилення ціни реалізованої ним продукції від рівня ринкової ціни може бути оцінений із використанням експоненціального закону розподілу ймовірностей, що має наступний вид:

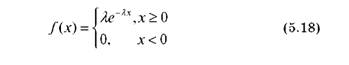
Інтегральна функція розподілу ймовірностей має вид:

У даному прикладі йдеться про те, що на ринку склалася ринкова ціна деякого продукту, що відповідає рівновазі попиту й пропозиції. Але підприємство надає переваги ризику і хоче або одержати додатковий дохід (прибуток) за рахунок підвищення (відхилення) цін запропонованої ним продукції відносно ринкової ціни, або збільшити реалізацію продукції, установлюючи на неї знижену ціну (рис. 5.7).

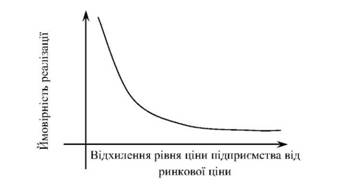
Рисунок 5.7 - Ймовірність реалізації без втрат у разі відхилення ціни підприємства від ринкової ціни

Розраховуючи на додатковий дохід (прибуток), підприємство водночас ризикує і може не одержати тих доходів, які б воно мало, торгуючи на ринку за існуючими цінами. Очевидно, резонно припустити, що чим більше відхилення цін, установлених підприємством на свою продукцію, від ринкових, тим більша ймовірність зростання можливих втрат. Але зауважимо, що зберігається й деяка ймовірність отримання додаткового доходу.

Характерним в основному для природних ризиків, фізичним розподілом є розподіл Парето (чи самоподібний розподіл). Функція щільності ймовірностей розподілу втрат при цьому має вид:

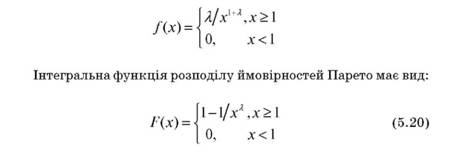
У теорії ймовірностей доведено, що функція розподілу суми великого числа незалежних випадкових величин близька до нормального розподілу за умови, що сукупність випадкових величин має кінцеві моменти першого і другого порядків. Це твердження зветься центральною граничною теоремою. Більшість ризиків виникає саме як результат дії великого числа незалежних випадкових факторів і тому може бути описано нормальним розподілом. Даній умові задовольняють відмовлення й аварії технічних систем, втрати на фінансовому ринку, ризики збитку життя і здоров'я тощо.

Самоподібний розподіл характерний для більшості природних катастроф, таких, як землетруси і повені.

З трьох описаних розподілів тільки самоподібний не має кінцевих центральних моментів першого і другого порядків.

Як середній рівень ризику може бути використане математичне очікування випадкової величини. Якщо функція не має моментів, то замість математичного очікування використовують медіану розподілу.

Як граничний рівень ризику, що був визначений як максимально прийнятний розмір втрат, може застосовуватися квантиль розподілу. Квантиль - це таке значення випадкової величини, що може бути перевищено лише з ймовірністю, яка менше заданої.

Квантиль порядку визначається як корінь рівняння:

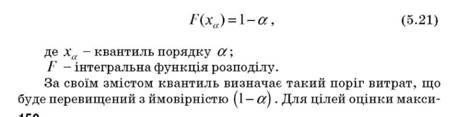
мальної величини втрат доцільно використовувати 95%, 99% чи навіть 99,9% квантилі, що відповідає ймовірності перевищення максимально прийнятного рівня витрат з частотою відповідно один раз у 20, 100 і 10 000 років.

Розглянемо дещо ускладнену ситуацію, коли підприємству доводитися оцінювати ризик у зв'язку зі зміною загальної кон'юнктури ринку. Так, є конкурентний ринок, де різко змінюється ситуація щодо попиту на продукцію, яку випускає підприємство. Крім нашого підприємства, таку ж продукцію випускають 8 підприємств. Можливе входження на ринок ще одного нового підприємства.

Потрібно оцінити, який ризик підприємства, якщо воно не прореагує на зміну кон'юнктури ринку. У даному разі обмежимося визначенням ймовірності того, які підприємства, що випускають конкуруючий із нашим продуктом товар, прореагують на зміну кон'юнктури і попиту ринку. Для спрощення розуміння суті справи припустимо, що ймовірність реакції кожного підприємства, у тому числі й нашого, на кон'юнктуру ринку, що змінилася, дорівнює 0,1. Будемо вважати, що можливість включення в ринок нового підприємства дорівнює 0,15. Разом на ринку даного продукту можуть бути 10 підприємств. Якщо хоча б одне підприємство, крім того, що досліджується, відреагує на ситуацію швидше, ніж ми, то нашому підприємству загрожують втрати в сумі 400 млн. грн.

Оцінити ймовірність цих втрат можна виходячи з теореми про ймовірність появи хоча б однієї з п незалежних подій:

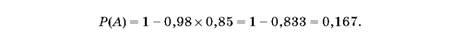
Отже, якщо ми не відреагуємо раніше інших на кон'юнктуру ринку, що змінилася, ймовірність виникнення втрат у розмірі приблизно 400 млн. грн. для підприємства, що досліджується, досить велика - 0,167.

Для оцінки ризику в діяльності підприємства потрібна достовірна інформація, яку можна мати тільки в результаті її накопичування й систематизації. Цінова інформація, особливо в умовах інфляції, вимагає постійного поповнення й опрацювання щодо нових ризиків. Для аналізу ризикових показників вона потребує статистичного опрацювання. Але часто її буває недостатньо. Тому доводитися користуватися експертними оцінками. Отже, інформацію з визначення ризику варто умовно поділити на два види:

об'єктивна, або статистична, інформація, що може бути використана для розрахунку ймовірних характеристик оцінки ризику;

суб'єктивні, експертні оцінки, що є пропозиціями експертів, фахівців. Нерідко інтуїтивні оцінки можуть сприяти виробленню найбільш вдалого рішення.

Ймовірна оцінка ризику математично відпрацьована, має свої теореми та методи обчислення, але задовольнятися цим у підприємницькій діяльності теж досить ризиковано, через те що реальна точність математичного розрахунку багато в чому залежить від вихідної інформації. Тому й тут не можна відмовлятися від підприємницької інтуїції.

Питання для поточного контролю та поглибленого засвоєння знань

1. Розкрийте поняття "оцінка ризику".

2. Охарактеризуйте області ризику.

3. Охарактеризуйте зони ризику.

4. В чому полягає сутність поняття рівня ризику?

5. Чим обумовлена відсутність універсальної методики визначення економічного ризику?

6. В чому полягає сутність нормального розподілу випадкових величин?

7. Охарактеризуйте параметри нормального розподілу.

8. Як побудувати криву ризиків?

9. Сформулюйте загальні умови приємності певного виду економічної діяльності.

10. Чим обумовлено використання кількісної оцінки ризику для ухвалення господарського рішення?

11. Охарактеризуйте види втрат в підприємницькій діяльності.

12. Чим обумовлено розподіл на зони ризику і в чому полягають особливості кожної зони ризику?

13. Яким чином змінюється структура втрат у залежності від виду підприємницької діяльності?

14. Наведіть приклади розподілу рішень щодо управління ризиком для подій різного класу.