Обгрунтування господарських рішень та оцінювання ризиків - Донець Л.І. - 9.3. Використання "дерева рішень"

для обґрунтування господарських рішень

Метод дерева рішень - це один з методів автоматичного аналізу величезних масивів даних. Перші ідеї створення "дерев рішень" починаються з робіт П.Ховленда і Е.Ханта кінця 50-х років XX століття. Проте основоположною роботою, що дала імпульс для розвитку цього напряму, стала книга Е.Ханта, Дж.Мерина і П.Стоуна "Experiments in Induction", яку було опубліковано в 1966 р.

Область використання методу "дерева рішень" можна об'єднати в три класи:

опис даних: застосування "дерева рішень" дозволяє зберігати інформацію про вибірку даних в компактній і зручній для обробки формі, що містить в собі точні описи об'єктів;

класифікація: застосування "дерева рішень" дозволяє справитися із завданнями класифікації, тобто відношення об'єктів до одного з описаних класів;

регресія: якщо змінна має недостовірні значення, то застосування "дерева рішень" дозволяє визначити залежність цієї цільової змінної від незалежних (вхідних) змінних.

Для прийняття рішення за допомогою "дерева рішень" необхідно виконати такі крокі:

1) оцінити стан ринку вектором чинників X = (x1, x2, x3, x4) (цей крок виконується користувачем системи);

2) визначити клас зростання прибули шляхом руху вектора X = (x1, x2, x3, x4) по дереву рішень з верхніх рівнів до нижніх (цей крок виконується системою).

У методиці використовується ієрархічна структурна схема. Для її побудови прийняті відповідні позначення елементів (подій) і логічних операцій.

В основу методу "дерева цілей" покладено підпорядкованість, розгортаємість і ранжування цілей. Дерево цілей з кількісними показниками, що використовуються в якості одного із засобів при прийнятті рішень, і носить назву "дерева рішень".

Головна перевага "дерева рішень" перед іншими методами - можливість пов'язати ставлення цілі з діями, що підлягають реалізації в сьогоденні. При побудові багаторівневого "дерева рішень" досягнення мети кожного з рівнів моделі забезпечується комплексом заходів попереднього рівня. Кожен рівень "дерева рішень" повинен займати певне місце в ієрархічній послідовності, складеної на основі дотримання причинно-наслідкових зв'язків.

9.3.1. Етапи побудови "дерева рішень"

Дерево рішень - це графічне зображення послідовності рішень і станів середовища з указівкою відповідних ймовірностей і виграшів для будь-яких комбінацій альтернатив і станів середовища.

Побудова "дерева рішень" виконується "зверху вниз" - від задач більш складних, більш важливих - до завдань менш складним, менш важливим, що вимагає менше часу (коштів, сил, ресурсів) для їх здійснення.

На схемі "дерева рішень" саме верхнє положення займає кінцева мета розв'язання проблеми (кінцевий результат).

Чим складніше можна вирішити завдання, тим більше має бути число рівнів розгляду проблеми і тим більше число завдань, що вирішуються на кожному рівні.

Для кожного "дерева рішень" будується матриця. Часто вводяться коефіцієнти взаємної корисності рішень, одержувані опитуванням експертів. Вони показують вплив ступеня важливості одних рішень на інші.

Застосування методу "дерева рішень" дозволяє:

визначати шляхи досягнення мети з виконанням кількісної оцінки складності виникають завдань та оцінкою труднощі здійснення того чи іншого варіанту;

поліпшувати якість рішень в умовах невизначеності.

Процес прийняття управлінських рішень за допомогою дерева рішень у загальному випадку припускає виконання п'яти етапів:

Етап 1. Формулювання завдання.

Насамперед необхідно відкинути всі фактори, що не стосуються проблеми, а серед безлічі тих, що залишилися, виділити суттєві і несуттєві. Це дозволить привести опис завдання щодо прийняття управлінського рішення у форму, що піддається аналізу. Повинні бути виконані такі основні процедури: визначення можливостей збору інформації для експериментування і реальних дій;

складання переліку подій, що з певною імовірністю можуть відбутися;

установлення часового порядку розміщення подій, у наслідках яких міститься корисна і доступна інформація, і тих послідовних дій, які можна розпочати.

Етап 2. Побудова "дерева рішень".

Етап 3. Оцінка ймовірностей станів середовища, тобто зіставлення шансів виникнення кожної конкретної події. Слід зазначити, що вказані ймовірності визначаються або на підставі наявної статистики, або експертним шляхом.

Етап 4. Установлення виграшів (чи програшів, як виграшів зі знаком мінус) для кожної можливої комбінації альтернатив (дій) і станів середовища.

Етап 5. Вирішення завдання.

Перш ніж продемонструвати процедуру застосування дерева рішень, введемо ряд визначень. У залежності від ставлення до ризику розв'язання задачі може виконуватися з позицій так званих "об'єктивістів" і "суб'єктивістів".

Безумовним грошовим еквівалентом (БГЕ) гри називається максимальна сума грошей, які гравець готовий заплатити за участь у грі (лотереї), або, що те саме, та мінімальна сума грошей, за яку він готовий відмовитися від гри.

Кожен гравець має свій БГЕ. Гравця, для якого БГЕ збігається з очікуваною грошовою оцінкою (ОГО) гри (з середнім виграшем у грі), тобто виконується рівність

то гравця умовно називають об'єктивістом; якщо рівність (9.1) не виконується, то гравця, для якого БГЕ менше або більше ОГО, називають суб'єктивістом.

Очікувана грошова оцінка розраховується як сума добутків розмірів виграшів на ймовірності цих виграшів, тобто ОГО співпадає з математичним очікуванням випадкової величини Х - величини виграшів. Якщо х1,х2,...,хn - можливі значення випадкової величини Х, а р1,р2,...,рn - ймовірності, з якими випадкова величина Х приймає можливі значення, тоді ОГО можна знайти за формулою

Приклад 9.1. Проводиться розіграш лотереї, в якій розігрується 100 білетів. З них 5 мають виграш 50 грн., 10 - 10 грн., інші виграшу не мають. Вартість одного лотерейного білету 1 грн. Розрахувати ОГО для виграшу гравця та проаналізувати гравця з позиції БГЕ.

Розв язання. Для того, щоб розрахувати ОГО побудуємо випадкову величину Х - величину виграшу в лотереї. Наприклад, якщо гравець придбає білет, і він не виграє, то гравець витратить 1 грн., тому його виграш буде дорівнювати втраченій 1 грн., тобто х1 =-1. З аналогічних міркувань отримаємо, що випадкова величина Х буде мати такі можливі значення: х1 = -1, х2 = 9 , х3 = 49 . За класичним означенням ймовірності знайдемо ймовірності можливих значень: р1 = 0,85 , р2 = 0,1, х3 = 0,05 . Таким чином маємо закон розподілу випадкової величини Х, що наведено в табл.

Таблиця 9.3. Закон розподілу виграшу в лотереї

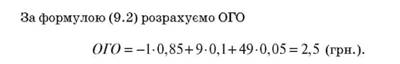
Один індивід пошкодує і 1 грн. за право участі в такій лотереї, тобто просто не купить лотерейний білет, інший готовий заплатити за лотерейні білети 5 грн., а третій заплатить навіть 30 грн. за можливість одержати 50 грн. (наприклад, коли ситуація складається так, що тільки маючи 50 грн., гравець може досягти своєї мети, тому можлива втрата останніх коштів, а в нього їх рівно 30 грн., не змінює для нього ситуації).

Якщо БГЕ гри дорівнює 2,5 грн., то гравця можна назвати об'єктивістом; якщо БГЕ гри менше ніж 2,5 грн., то гравець є суб'єктивістом, який не схильний до ризику; якщо БГЕ гри більше ніж 2,5 грн., то гравець є суб'єктивістом, який схильний до ризику.

9.3.2. Процедура прийняття господарського рішення за допомогою "дерева рішень"

Розглянемо процедуру прийняття управлінського рішення на прикладі наступної задачі.

Приклад 9.2. Керівництво компанії вирішує, чи створювати для випуску нової продукції велике підприємство, мале підприємство чи продати патент іншій фірмі. Розмір виграшу, який компанія може одержати, залежить від сприятливого чи несприятливого стану ринку (табл. 9.4).

За допомогою дерева рішень надати рекомендації щодо прийняти управлінського рішення.

Розв'язання. На основі даної таблиці виграшів (втрат) можна побудувати "дерево рішень" (рис. 9.8).

Ймовірність сприятливого і несприятливого станів економічного середовища дорівнює 0,5. Процедура прийняття управлінського рішення полягає в обчисленні для кожної вершини дерева очікуваних грошових оцінок, відкиданні безперспективних галузей і виборі галузей, яким відповідає максимальне значення ОГО.

Таблиця 9.4. Вихідні умови прикладу 9.2

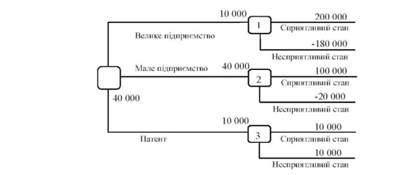
Рисунок 9.8 - Дерево рішень для прикладу 9.2

Порівнявши розраховані ОГО, можна зробити такий висновок.

Найбільш доцільно вибрати стратегію 2, тобто будувати мале підприємство, а галузі (стратегії) 1 і 3 дерева рішення можна відкинути. ОГО найкращого рішення дорівнює 40000 у.о. Слід зазначити, що наявність стану з ймовірностями 50% (або 0,5) невдачі і 50% удачі на практиці часто означає, що справжні ймовірності гравцю швидше за все невідомі і він приймає таку гіпотезу (так зване припущення - п'ятдесят на п'ятдесят).