Обгрунтування господарських рішень та оцінювання ризиків - Донець Л.І. - 12.2. Принцип мінімаксу (максиміну). Розв'язок матричної гри в чистих стратегіях

Визначимо найкращу стратегію гравця А з урахуванням всіх можливих відповідей на неї гравця В. При цьому слід розраховувати на те, що на будь-яку стратегію Аі гравця А гравець В відповість стратегію Вj, для якої виграш гравця А виявиться мінімальним, оскільки гравець В прямує зашкодити гравцю А.

Алгоритм знаходження максиміну (мінімаксу)

Максимін - це максимальний виграш, який гравець А може собі гарантувати в грі проти розумного противника.

Якщо гравець А буде дотримуватись максимінної стратегії, то йому при будь-якої розумної поведінці гравця В гарантовано виграш, не менший ніж а.

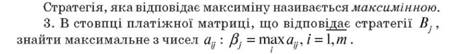
Мінімакс - це мінімальний програш, який гравець В може собі дозволити в грі проти розумного противника.

Якщо гравець В буде дотримуватись найбільш обережної з усіх стратегій - мінімаксної - то йому при будь-якої випадку забезпечено програш, не більший ніж в.

Стратегія, яка відповідає мінімаксу називається мінімаксною.

Принцип мінімаксу. В теорії ігор принцип обережності, який рекомендує гравцям дотримання максимінної і мінімаксної стратегій, називається принцип мінімаксу. Він випливає з припущення про обережність гравців, тобто з бажання розв'язати конфліктну ситуацію найкращим чином для всіх учасників конфлікту.

Приклад 12.3. Проаналізувати платіжну матрицю, яку побудовано у прикладі 12.2. Визначити верхню і нижню ціну гри.

Розв' язання. Запишемо платіжну матрицю у вигляді таблиці 12.3.

Таблиця 12.3. Платіжна матриця гри

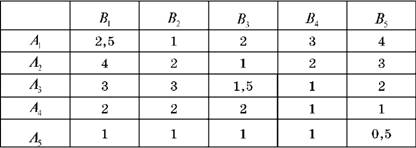
Проаналізуємо гру з боку фірми В, яка контролює стовпці платіжної матриці. Перший стовпець, що відповідає стратегії В1, є гіршим ніж інші, оскільки фірмі В він несе найбільший програш. Фірмі В стратегію В1 не зручно застосовувати (говорять, що це домінуюча стратегія), тому її можна виключити з платіжної матриці:

Таблиця 12.4. Платіжна матриця гри без стратегії В1

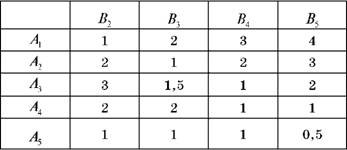
Проаналізуємо гру з боку фірми А, яка контролює рядки платіжної матриці. Останній рядок, що відповідає стратегії А5 є гіршим ніж інші, оскільки фірмі А він несе найменший виграш. Фірмі А стратегію А5 не зручно застосовувати, тому її можна виключити з платіжної матриці:

Таблиця 12.5. Платіжна матриця гри без стратегій В1, А5

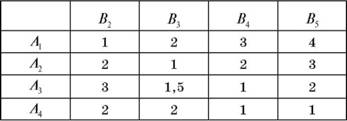
Фірма В не буде застосовувати стратегію В5, оскільки вона домінується стратегією В4, при виборі якої програш цієї фірми менше. Тому стратегію В5 можна виключити з платіжної матриці:

Таблиця 12.6. Платіжна матриця гри без стратегій В1, А5, В5

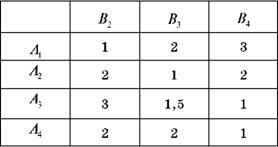
Після скорочення розміру платіжної матриці гри, визначимо верхню і нижню ціну гри за допомогою алгоритму знаходження максиміну (мінімаксу). В кожному рядку платіжної матриці знайдемо мінімальне з чисел aij і запишемо його у додатковий стовпчик min ajj.

Таблиця 12.7 Платіжна матриця гри без стратегій B1, A5 , B5

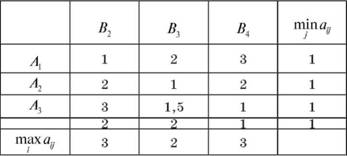
З найдених чисел виберемо найбільше за формулою (12.5) а = vнц = max аi = max {1,1,1,1} = 1, що визначить нижню ціну гри або максимін, тобто максимальний виграш, який фірма А може собі гарантувати в грі, що розглядається. Цей виграш відповідає стратегіям A1, A2, A3 і A4. Тобто кожна стратегія фірми А є мак-симінною.

В кожному стовпці платіжної матриці знайдемо максимальне з чисел aij і запишемо його у додатковий рядок max aij.

З найдених чисел виберемо найменше за формулою (12.6) ß = vвц = minßj = min {3, 2, 3} = 2 , що визначить верхню ціну гри або мінімакс, тобто мінімальний програш, який фірма В може собі дозволити в грі, що розглядається, який відповідає стратегії B3. Ця стратегія є мінімаксною.

Таким чином, скоротити розмірність платіжної матриці можна:

виключенням однакових рядків чи стовпців;

виключенням більших стовпців

виключенням менших рядків.

В матричній грі, яку розглянуто в прикладі 12.3, верхня і нижня ціни гри не співпадають: vнц ≠ vвц.

Якщо верхня і нижня ціни гри співпадають, то загальне значення vнц = vвц = v називається чистою ціною гри або ціною гри, а така гра називається визначеною грою в чистих стратегіях або грою з сідловою точкою.

Чистою стратегією Ai гравця А називається можливий хід, який гравець А обрав з ймовірністю 1.

Ціна гри v дорівнює елементу платіжної матриці (aiojo).

Елемент (aiojo) є одночасно мінімальним в рядку io платіжної матриці, максимальним в стовпці jo платіжної матриці і називається сідловою точкою. Сідловій точці відповідають оптимальні стратегії, сукупність яких є оптимальним рішенням або рішенням матричної гри.

Якщо один з гравців дотримується своєї оптимальної стратегії, то для другого гравця відхилення від його оптимальної стратегії не може бути вигідним. Відступ гравців від їхніх оптимальних стратегій погіршує їх власне становище.

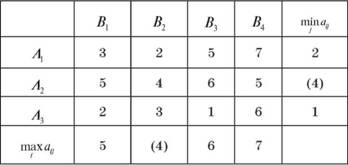
Розв'язання. Запишемо платіжну матрицю у вигляді таблиці 12.8.

Таблиця 12.8. Платіжна матриця гри