Теорія економічного аналізу - Купалова Г.І. - 13.2. Програмування

Математичне або оптимальне програмування розробляє теорію та методи вирішення умовних екстремальних задач і є основою формального апарату аналізу різноманітних задач управління, планування та проектування. Особливо велику роль відіграє програмування в задачах оптимізації планування суспільного господарства та управління виробництвом. Завдання планування економіки здебільшого зводяться до вибору сукупності чисел (параметрів управління), які забезпечують оптимум деякої функції при обмеженості умов роботи системи.

Залежно від властивостей функцій, які визначають показник якості та обмеження задачі, математичне програмування поділяється на лінійне та нелінійне.

Задачі, в яких цільова функція є лінійною, а умови записуються у вигляді лінійних рівностей та нерівностей, становлять предмет лінійного програмування. Задачі, в яких показник якості рішення або деякі із функцій, що визначають обмеження нелінійні, належать до нелінійного програмування.

Метод лінійного програмування найбільш розповсюджений у прикладних економічних дослідженнях завдяки його достатній наочності, зрозумілості інтерпретацій. Це дає змогу суб'єкту господарювання прийняти найкраще обґрунтоване (за формальними ознаками) рішення в умовах більш-менш жорстких обмежень стосовно доступних для підприємства ресурсів. Особливо ефективне застосування лінійного програмування в аналізі фінансово-господарської діяльності для вирішення насамперед завдань щодо планування діяльності для пошуку оптимальних параметрів випуску та найкращого використання наявних ресурсів.

Отже, сутність методу лінійного програмування полягає у пошуку максимуму чи мінімуму обраної відповідно до мети аналізу цільової функції за наявних обмежень.

Проведення економіко-математичного моделювання передбачає 3 основні етапи:

1) постановка мети і визначення завдань дослідження, якісний опис об'єкта у вигляді економічної моделі;

2) формування математичної моделі досліджуваного об'єкта, вибір чи розробка методів дослідження, програмування моделі на ЕОМ, підготовка вихідної інформації;

3) аналіз математичної моделі, здійснення розрахунків, обробка та аналіз отриманих результатів.

Розглянемо чим є модель. Модель (лат. modulus – міра, зразок) – абстрактний образ, який відображає основні риси описуваного явища. Оскільки модель відтворює сутність відповідного об'єкта, вона відтворює й об'єкт, відволікаючись при цьому від другорядних властивостей, які реально властиві досліджуваному об'єкту. Тому модель ніколи повністю не є адекватною об'єкту і передбачає використання процедур абстрагування та ідеалізації.

Терміном "модель" позначають також аналог досліджуваного процесу, предмета чи явища, що відображає суттєві функції та характеристики об'єкта, який моделюється, з погляду мети дослідження.

Під економіко-математичною моделлю слід розуміти математичний опис досліджуваного економічного процесу чи об'єкта. Здебільшого математична модель будь-якого процесу в економіці характеризується за допомогою системи рівностей та нерівностей, які містять певний набір параметрів і змінних величин. Процедура економіко-математичного моделювання замінює дорогі та трудомісткі натуральні експерименти розрахунками.

Розглянемо використання методу лінійного програмування на прикладі.

Приклад. Для виготовлення двох видів кондитерської продукції – печива та цукерок – використовують чотири види сировини: наповнювач, цукор, какао-порошок, муку. Запаси та кількість сировини, яка витрачається кондитерським цехом на виготовлення однієї тонни виробів наведені в табл. 13.2.

Прибуток, який отримують з 1 т печива дорівнює 750 грн, а з тонни цукерок – 1200 грн.

Визначити оптимальні річні обсяги виробництва печива і цукерок, щоб прибуток від їх реалізації був максимальний за наявних ресурсів.

Таблиця 13.2. Ресурси та витрати на виготовлення продукції кондитерського цеху

Розв'язання

1. Складемо економіко-математичну модель задачі. Для цього позначимо обсяг виробництва печива як х1% а цукерок як х2. Для їх виготовлення потрібно буде:

– наповнювача: 0,1х₁ + 0,3х₂;

– цукру: 0,2х₁ + 0,1х₂;

– какао-порошку: 0,1х₂;

– муки: 0,3х₁.

Оскільки споживання сировини не повинно перевищувати її запаси, відповідно: 180,160, 50 і 210 т, то зв'язок між використанням сировини та її запасами відобразить система нерівностей:

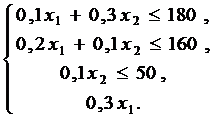
За змістом задачі змінні величини х₁³ 0, х₂³0.

2. Загальний прибуток (П) становитиме 1500 х₁ грн від реалізації печива та 2500 х₂ грн від реалізації цукерок, тобто

П = 750х₁ +1200х₂ max.

3. Розрахуємо х₁ та х₂.

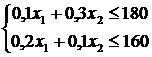p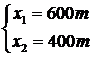

Таким чином, оптимальний річний обсяг виробництва для отримання максимального прибутку становить для печива – 600 т, цукерок – 400 т. За таких умов очікується одержання прибутку розміром 930 тис. грн:

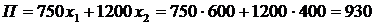(тис. грн).