Теорія економічного аналізу - Купалова Г.І. - 13.4. Метод Монте-Карло

Поєднання аналізу чутливості та методу сценаріїв на основі теорії ймовірностей здійснюється в імітаційному моделюванні за методом Монте-Карло.

Метод Монте-Карло – це чисельний метод, основу якого становить одержання великого числа реалізацій випадкового процесу, який формується так, щоб імовірнісні характеристики (математичні очікування, імовірність деяких подій, імовірність попадання траєкторії процесу в деяку область тощо) дорівнювали певним величинам задачі, яка розв'язується.

Метод Монте-Карло ґрунтується на імітації масового процесу шляхом вирахування його ходу, в якому випадкові коливання визначаються за допомогою жеребка або таблиці випадкових чисел. Економічний експеримент може замінюватися статистичними випробуваннями моделі економічного процесу. Побудова цієї моделі може ґрунтуватися на розподілі випадкових величин у досліджуваному процесі.

Таким чином, сутність методу Монте-Карло полягає в тому, що замість аналітичного описання системи масового обслуговування здійснюється "розіграш" випадкового процесу, який відбувається в системі масового обслуговування, шляхом спеціально організованої процедури. В результаті такого "розіграшу" здійснюється кожного разу нова, відмінна від інших реалізація випадкового процесу. Цю множину реалізацій можна використати як деякий штучно отриманий статистичний матеріал, що обробляється звичайними методами математичної статистики. Після такої обробки можуть бути отримані майже будь-які характеристики обслуговування.

В імітаційному моделюванні за методом Монте-Карло передбачається певна послідовність та етапність дослідження (рис. 13.3).

Перший етап імітаційного моделювання за методом Монте-Карло. Розробка прогнозної моделі передбачає формування очікуваної імітаційної моделі, яка повинна адекватно відображати майбутній сценарій реалізації проекту.

Другий етап – виявлення чинників ризику включає відбір ключових змінних для моделювання.

Третій етап – визначення умов кореляції полягає у встановленні формальної залежності між результативним показником і відібраними ключовими змінними.

Четвертий етап – імовірнісний розподіл відібраних ключових змінних передбачає здійснення таких кроків:

1) визначення обмежень можливої зміни відібраних ключових змінних;

2) встановлення імовірнісної ваги за межами значень.

П'ятий етап – імітаційне прогнозування вимагає генерування випадкових сценаріїв реалізації проекту з використанням вибраних допущень.

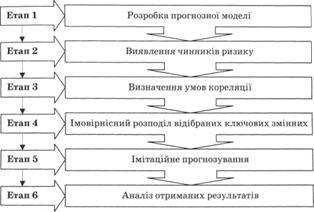
Рис. 13.3. Блок-схема імітаційного моделювання за методом Монте-Карло

Шостий етап – аналіз отриманих результатів потребує здійснення статистичної оцінки та інтерпретації одержаних результатів імітації.

Імітаційне моделювання за методом Монте-Карло застосовується для побудови математичної моделі для інвестиційного проекту з важкопрогнозованими показниками. Його метою є визначення розподілу результатів реалізації проекту на основі імовірнісного розподілу його ключових змінних і кореляційної залежності між ними.

Особливістю та однією з основних вимог імітаційного моделювання за методом Монте-Карло є застосування спеціальних комп'ютерних програм. Це, зокрема, пояснюється тим, що генерування випадкових сценаріїв реалізації проекту (етап 5) повторюються 500–1000 разів.

Одержані значення результативного показника проекту (чистої теперішньої вартості чи внутрішньої норми дохідності) використовуються для побудови графіка щільності його розподілу зі своїм власним математичним очікуванням і стандартним відхиленням. На основі значення математичного очікування та стандартного відхилення обчислюється коефіцієнт варіації результативного показника проекту, за допомогою якого оцінюється індивідуальний ризик проекту.

Метод Монте-Карло застосовується в розрахунках для складних комплексів, в яких використання класичних методів розрахунків практично неможливе. Він набув поширення у розв'язанні економічних задач, дослідженні функціонування складних систем, наприклад в теорії масового обслуговування, управлінні та нормуванні запасів та ін.

Наприклад, для вирішення питання щодо розширення магазину необхідно проаналізувати черги, які тут виникають. Час підходу покупців і час їх обслуговування мають випадковий характер і їх розподіл може бути встановлений за наявною інформацією. Внаслідок взаємодії цих випадкових процесів створюється черга.

Згідно з методом Монте-Карло перебирають (за допомогою ЕВМ) усі можливі стани системи з різним числом покупців за годину, часом їх обслуговування тощо, зберігаючи ті самі характеристики розподілу. В результаті багаторазового штучного відтворення роботи магазину розраховують характеристики обслуговування так, якби вони були одержані при спостереженні над реальним потоком покупців.