Логіка - Дуцяк І.3. - 5.2. Безпосередні виводи

Безпосередніми називають виводи, які містять один засновок. Далі йдеться про виводи, можливість виконання яких зумовлена тим чи іншим відношенням між обсягами імен, зафіксованих засновком.

Суть безпосередніх виводів полягає в такому. На підставі знання про відношення обсягу імені 5 до імені Р, заданого в явній формі у засновку, роблять явним неявно задане знання про відношення обсягу імені Р до обсягу імені 5 (такий вивід називають оберненням), про відношення обсягу імені Р до обсягу імені 5 (це протиставлення предикатові), про відношення обсягу імені 5 до обсягу імені Р (це називають перетворенням) та ін. Наприклад, у разі обернення з твердження Жодне озеро не є морем отримують твердження Жодне море не є озером.

Одним зі способів обґрунтування висновків у разі безпосередніх виводів є з'ясування виду відношення між шуканими іменами шляхом побудови діаграми відношення обсягів. Послідовність дій у цьому разі є такою.

Інструменти. Алгоритм виявлення висновку в разі одного засновку шляхом побудови діаграми Ейлера:

1- Будують діаграму відношення обсягів для засновку.

2. У разі, якщо шуканий висновок містить терміни з запереченнями, то діаграму відношень обсягів доповнюють полями, що відповідають обсягам заперечених імен.

3. Візуально визначають відношення обсягів між суб'єктом та предикатом шуканого висновку.

4. Формулюють відповідне знайденому відношенню твердження (у тому числі в словесному вигляді).

Розглянемо як засновок твердження Усі квадрати (5), але не тільки вони є прямокутниками (Р). Нехай треба побудувати висновки про відношення прямокутників до квадратів (обернення) і про відношення не прямокутників до квадратів (протиставлення предикатові).

Виконаємо обернення. Побудуємо діаграму відношення обсягів для засновку. Загально стверджувальному видільному вислову відповідає відношення підпорядкованості. Візуально визначаємо відношення шуканого суб'єкта до шуканого предиката - це відношення відповідає частковому видільному твердженню. Формулюємо відповідний цій діаграмі висновок: Частина Р і тільки вони є Б (рис. 5.5, 6"). Останнім кроком є формулювання цього висновку словесно: Частина прямокутників і тільки вона є квадратами.

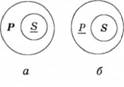
Рис. 5.5. Діаграми Ейлера, якими графічно зображено побудову висновку в разі обернення загальностверджувального невидільного засновку: а - діаграма засновку; б - діаграма висновку; підкресленням позначено ту підмножину об'єктів, яка є суб'єктом твердження

У разі побудови висновку про фігури, які не є прямокутниками (протиставлення предикату), відповідно до пункту 2 алгоритму, діаграму засновків треба доповнити зображенням тих об'єктів, які відповідають імені з запереченням (рис. 5.6, а). Якщо прямокутники на діаграмі Ейлера позначено колом з позначенням 3, то плоскі фігури, які не є прямокутниками, позначимо прямокутним полем поза межами кола Р. У висновку це поле повинно бути суб'єктом твердження.

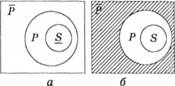
Рис. 5.6. Діаграми Ейлера, якими графічно зображено побудову висновку в разі протиставлення предикатові загальностверджувального засновку: а - діаграма засновку; б - діаграма висновку; штрихуванням позначено ту підмножину об'єктів, яка є суб'єктом висновку

Візуально визначаємо відношення шуканого суб'єкта до шуканого предиката - оскільки поле Р і поле 5 (див. рис. 5.6, а) не мають жодної спільної точки, то це відношення несумісності, якому відповідає загальнозаперечне твердження. Формулюємо відповідний цій діаграмі висновок Усі Р не є Я (див. рис. 5.6, б). Останнім кроком є формулювання цього висновку словесно: Жодна плоска фігура, яка не е прямокутником, не є квадратом.

Під час виконання безпосередніх виводів важливо враховувати, що для цих виводів актуальними є лише суб'єкт і предикат твердження, а не, скажімо, назви предметів. Наприклад, у разі, коли треба виконати обернення засновку Жоден орел не полює на муху у висновку треба стверджувати не про мух, а про тих, хто полює на мух. Отже, в разі обернення отримаємо: Жоден, хто полює на мух, не є орлом.

У традиційній логіці, зазвичай, описують три види безпосередніх виводів: перетворення, обернення і протиставлення предикатові. Водночас можливі інші варіанти відношень одного з імен 5 або 5 до обсягу одного з двох інших імен Р або Р, чи навпаки, одного з імен Р або Р до обсягу одного з двох інших імен 5 або 5. Є вісім варіантів таких відношень. Отже, якщо один із цих восьми варіантів є засновком (твердження зі структурою в - Р), то сім інших варіантів будуть можливими висновками: 5 - Р; 8 -Р; 5 - Р; Р -Я; Р - £; Р-5; Р - 5.

Сформулювати правило виведення будь-якого з наведених вище семи типів для довільного з п'ятнадцяти елементарних простих висловів можна за допомогою табличного методу.