Логіка - Жеребкін В.Є. - 9.1. Умовно-категоричний силогізм

(продовження)

9.1. Умовно-категоричний силогізм

Умовним силогізмом називається силогізм, у якому один або обидва засновки є умовними судженнями. Розрізняють два види умовних силогізмів: умовно-категоричний силогізм і чисто умовний силогізм.

Умовно-категоричним силогізмом називається силогізм, у якому більший засновок є судженням умовним, а менший — категоричним. Наприклад:

Якщо правовідносини належать до цивільного права, то суперечка підлягає судовому розгляду. Ці правовідносини належать до цивільного права. Отже, суперечка у цьому випадку має бути розв'язана у судовому порядку.

Логічною основою висновків умовнокатегоричного силогізму є така аксіома: ствердження основи неодмінно призводить до ствердження наслідку, а заперечення наслідку — до заперечення основи.

Це положення виражає такий об'єктивно існуючий зв'язок між причиною і наслідком: 1) певна причина неодмінно викликає певний наслідок і 2) наслідок не може виникнути без причини з нічого. Тому, якщо існує причина, то має існувати і її наслідок; якщо гаданий наслідок не існує, то це означає, що не існує й причини, котра викликає цей наслідок. Наприклад, якщо тіло нагріти (причина), то воно обов'язково розшириться (наслідок), а якщо цей наслідок відсутній, то відсутня його причина (нагрівання).

Подібну умовну залежність ми спостерігаємо також між явищами співіснуючими та явищами, пов'язаними у певній послідовності у часі.

Залежно від того, який хід руху думки від ствердження основи до ствердження наслідку або від заперечення наслідку до заперечення основи, розрізняють два модуси умовно-категоричного силогізму: стверджуючий та заперечний.

Стверджуючий модус (modus ponens) — це такий умов-no-категоричний силогізм, у якому в меншому засновку стверджується основа, а у висновку — наслідок більшого засновку. Формула модусу:

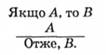
За допомогою символів математичної логіки цей модус відображають так:

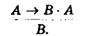
У стверджуючому модусі від істинності (існування) основи ми йдемо до істинності (існування) наслідку. Хід умовиводу тут ґрунтується на положенні: ствердження основи веде до ствердження наслідку.

Менший засновок стверджуючого модусу за якістю не обов'язково є ствердним, він може бути й заперечним. Згідно з цим стверджуючий модус має такі чотири різновиди:

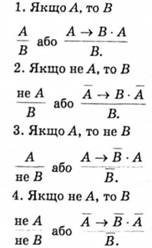
Заперечний модус (modus tollens) — це такий умовно-категоричний силогізм, у котрому у меншому засновку заперечується наслідок, а у висновку — основа більшого засновку, Формула модусу:

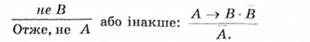
У заперечному модусі у меншому засновку заперечується істинність (існування наслідку) більшого засновку, йдеться про те, що в цьому випадку немає такого наслідку, котрий указано в умовному судженні. У висновку висловлюється думка про те, що в цьому випадку не було (або немає) і самої основи більшого засновку. Наприклад:

У заперечному модусі ми робимо висновок від хибності (відсутності) наслідку до хибності (відсутності) основи. Такий рух думки визначається положенням (аксіомою): заперечення наслідку є заперечення основи.

Обидва розглядувані модуси (стверджуючий і заперечний) правильні, їх висновки, що випливають із засновків неминуче, — достовірні. Правомірним є запитання: чи можна в умовно-категоричному силогізмі робити висновок від хибності основи до хибності наслідку і від істинності наслідку до істинності основи? Відповідь на це запитання логіка дає негативну. Зумовлено це ось чим. Зв'язок причини й наслідку

(дійсності), як правило, неоднозначний. Один і той же наслідок може бути викликаний не однією, а різними причинами. Наприклад, пожежа (наслідок) може виникнути унаслідок підпалу, через несправність електропроводки, удару блискавки, якогось нещасного випадку; подряпини та садна на тілі підозрюваного можуть бути наслідком його боротьби з жертвою, але можуть бути й наслідком якоїсь іншої причини.

Схематично відношення причини і наслідку можна відобразити так:

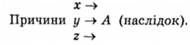
Якщо цю схему виразити у вигляді суджень, то висловимо три такі умовні судження:

Із наведеного видно також, що якщо немає, наприклад, причини х, то це ще не означає, що нема й наслідку А; воно могло бути викликане причиною у або причиною z. А якщо існує наслідок А, то з цього неминуче не випливає, що в цьому випадку існує причина х; наслідок міг бути результатом причини у або z. Тому умовиводи від заперечення даної основи до заперечення наслідку і від ствердження наслідку до ствердження певної основи дають знання не достовірні, а тільки більш-менш імовірні або хибні. Наприклад:

Тут у меншому засновку стверджується наслідок більшого засновку, тому не можна зробити істинного висновку про те, що даний договір укладений не в нотаріальній формі, він міг бути визнаний недійсним з якоїсь іншої причини, наприклад тому, що документи домовласника виявилися підробленими.

Висновки від існування наслідку до існування основи і від відсутності основи до відсутності наслідку не містять доказової сили, за їхньої допомоги не можна обґрунтувати кінцевих висновків із судової справи. Але, оскільки вони все ж можуть давати приблизні знання, ними часто користуються у практиці розслідування кримінальних справ під час висування версій.

Наприклад, на місці вчиненого злочину виявлено труп із слідами боротьби. Слідчий припускає, що сліди боротьби мають залишитися і на тілі злочинця. У ході розслідування справи стає відомо, що у Петренка на руках, обличчі і шиї наявні садна й подряпини. Природно припустити, що Петренко причетний до вчиненого злочину. Така версія з логічного боку є висновком від існування наслідку до існування основи:

Здобутий висновок тільки імовірний, оскільки садна у Петренка могли утворитися за обставин, котрі не пов'язані із цим злочином.