Логіка - Конверський А.Є. - 3. Визначення логічних термінів.

Таким чином, розгляд групи семантичних категорій, яку називають дескриптивними термінами, показує, що вони фіксують головні типи мислиннєвих структур, із яких будується процес міркування.

Самі ж логічні зв'язки, відношення, що мають місце у процесі міркування, представлені другою групою семантичних категорій - логічними термінами.

До л о г і ч н и х термінів відносять відношення1 між дескриптивними термінами у середині висловлювання, відношення між висловлюваннями, кількісні характеристики предметів думки у простих висловлюваннях, описові вирази предметів думки у простих висловлюваннях.

У природній мові відношення між термінами у простому висловлюванні, відношення між простими висловлюваннями у складному висловлюванні виражають, відповідно, словами "є" ("суть"), "і", "або", "якщо, то", "ні", "якщо, і тільки якщо, то". Відношення зафіксовані цими словами, називають л о г і ч н и м и зв'язками.

Кількісні характеристики предмета думки у простому висловлюванні виражають словами "будь-які" "всі", "деякі" і називають кванторами ("всі" - квантор загальності, "деякі" - квантор існування).

Описові вирази предмета думки у простому висловлюванні представлені словами "той", "який", "такий, що". Це - оператори визначених і невизначених дескприпцій.

Розглянемо стисло логічні зв'язки. До характеристик кванторів і операторів визначеної та невизначеної дескрипцій звернемося пізніше.

Серед групи логічних зв'язок виділяють зв'язку "є" і так звані пропозиційні зв'язки "і", "або", "якщо, то", "ні", "якщо і тільки якщо, то".

Зв'язка "є" (або множинна форма "суть"), як уже зазначалося, фіксує логічні відношення між дескриптивними термінами у простому висловлюванні. Вона констатує наявність певної ознаки у суб'єкта висловлювання. А оскільки ознаки бувають двох видів (властивість або відношення), то зв'язка "є" вказує на наявність у предмета думки певної властивості, або наявність між предметами думки певного відношення.

1. Варшава є столичним містом.

2. Сократ є вчителем Платона.

У першому висловлюванні зв'язка "є" приписує властивість предмета думки "столичне місто", у другому - відношення, яке притаманне Сократу і Платону.

Залежно від того, що констатує "є" у висловлюванні їх поділяють на:

- атрибутивні (висловлювання про властивості) і

-релятивні (висловлювання про відношення).

Щоб у даному випадку не виникло плутанини стосовно зв'язки "є" (тобто, що зв'язка "є" виражає відношення між S і Р, і тут же, що зв'язка "є" приписує відношення предмета думки висловлювання), то звернемо увагу на таку обставину.

Виходячи з того, що зв'язка "є" фіксує відношення між S і Р, а ці відношення можуть бути двох видів: або відношенням належності, або відношенням неналежності.

Відношення належності - це відношення простору, часу, величини, сили, причинності тощо. Наприклад, у висловлюванні "Логіка є філософською наукою" маємо відношення належності, а у висловлюванні "Логіка виникла раніше кібернетики" - маємо відношення часу. За логічним характером ці висловлювання різні. У першому констатується зв'язок між предметом і такою його ознакою, як властивість, а в другому - зв'язок між предметами через таку ознаку, як часове відношення.

Відношення належності має такі різновиди:

а) належність властивості предмета ("6 є парним числом");

б) належність певного предмета до класу предметів ("Ньютон є видатним фізиком");

в) належність одного класу предметів до іншого ("Трикутник є геометричною фігурою").

Отже, розуміння зв'язки "є" як відношення належності чи неналежності дає єдиний критерій логічного аналізу простих висловлювань, на якому ґрунтується логіка предикатів - один із розділів сучасної формальної логіки.

На відміну від зв'язки "є", слова природної мови "ні", "і", "або" , "якщо, то", "якщо і тільки якщо, то" складають групу логічних термінів, які фіксують логічні відношення не між Б і Р, а між висловлюваннями.

Слова "і", "або", "якщо, то" і подібні їм прийнято називати граматичними сполучниками. І це справді так, коли ми хочемо описати способи зв'язку простих речень у складні. За допомогою граматичних сполучників досягається певна смислова єдність простих речень у складному. Утворюючи складне речення зосереджуються на тому, щоб воно було зв'язане за змістом, не звертаючи уваги на те, істинні чи ні прості речення (що входять до його складу), а також отримане з них складне речення.

Але ці ж слова є носіями і логічних сполучників. На відміну від граматичних сполучників, логічні сполучники фіксують зв'язки між висловлюваннями, а не між реченнями.

Сполучаючи висловлювання за допомогою логічних сполучників, ми враховуємо лише логічні значення (істинність, хибність) простих висловлювань і відволікаємося від змісту, смислу простих висловлювань. При утворенні складних висловлювань нас цікавить залежність істинності чи хибності складного висловлювання від істинності чи хибності простих висловлювань, що його складають.

Наприклад, візьмемо висловлювання "Квадрат є геометричною фігурою або Франція є монархією". У цьому висловлюванні немає смислового, змістовного зв'язку, тому слово "або" не є носієм граматичного сполучника. Але з погляду логіки таке сполучення простих висловлювань допустиме і отримане з них висловлювання має конкретне значення. Тобто, отримане складне висловлювання ми оцінюємо як істинне.

Враховуючи цю особливість логічних сполучників (які у природній мові представлені тими самими словами, що й граматичні), у логіці вводяться спеціальні назви і символи для позначення логічних сполучників:

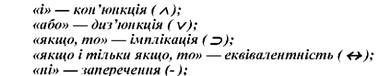
Оскільки логічні сполучники, з'єднуючи прості висловлювання у складні, фіксують не смисл, зміст простих висловлювань, а лише їхнє значення, то визначення кожного логічного сполучника зводиться, по суті, до встановлення умов, за яких утворене складне висловлювання буде істинним, а за яких - хибним. Іншими словами, пояснити, наприклад, що собою являє кон'юнкція, це означає показати, як залежить значення складного висловлювання від значень простих, що його утворюють за допомогою цього сполучника. А оскільки у складних висловлюваннях береться до уваги тільки значення простих, які комбінуються за допомогою логічних сполучників і це є визначальним, то, як правило, складне висловлювання часто називають за іменем сполучника, що його утворює. Тобто, говорять не "складне кон'юнктивне висловлювання", а "кон'юнкція".

За допомогою логічних сполучників із простих висловлювань утворюють складні, їх називають логічними операціями.

Розділ логіки, який досліджує природу таких логічних термінів, як заперечення, кон'юнкція, диз'юнкція, імплікація, еквівалентність, називають логікою висловлювань.

А логічні терміни "кон'юнкція", "диз'юнкція" і подібні - пропозиційними сполучниками, або пропозиційними зв'язками ("пропозиція" від слова висловлювання).

Отже, підсумовуючи попередні зауваження щодо характерних ознак пропозиційних сполучників, можна виділити два головних питанння, які цікавлять логіку висловлювань:

1) яким чином із простих (атомарних) висловлювань можна утворити складні (молекулярні) ?

2) як залежить логічне значення молекулярного висловлювання від логічних значень атомарних ?

Розглянемо тепер визначення пропозиційних зв'язок.

Серед пропозиційних зв'язок виділяють заперечення як унарну зв'язку . Унарна - означає "одномісна". Вона застосовується до одного висловлювання. Решта зв'язок (чотири), є бінарними, двомісними. Тобто, лише при наявності двох простих висловлювань можна отримати правильно побудоване складне висловлювання.

Запереченням називається логічна операція, за допомогою якої з певного істинного висловлювання отримують нове висловлювання, яке буде хибним, і навпаки.

Заперечне висловлювання складається із вихідного висловлювання і знака заперечення ( 1), який ставлять перед ним: 1 А. (Часто вживають і інші символи для позначення заперечення: ( - ) або ( ~ ). Відповідно: А або ~А. Запереченням висловлювання А є складне висловлювання 1 А. У природній мові аналогами заперечення є слова "не", "невірно, що", "не має місця, що".

У логіці висловлювань процедури визначення кожної логічної операції задаються так званими таблицями істинності.

Щоб побудувати таблицю істинності ми повинні прийняти такі умови:

1) просте висловлювання може бути або істинним, або хибним, але не можуть бути одночасно і істинним , і хибним;

2) кількість рядків таблиці істинності для певного складного висловлювання відповідає формулі: 2n (де 2 - кількість логічних значень для простого висловлювання (істина та хиба), а n - кількість простих висловлювань, що входять до складу складного висловлювання). Логічне значення "істина" позначається буквою "і" (перша буква в слові "істина"), а логічне значення "хиба" - буквою "х" (перша буква в слові "хиба").

Наприклад, якщо до складу складного висловлювання входить два простих висловлювання, то відповідно до формули 2n замість п підставляємо 2 і отримуємо формулу 22 = 4. Тобто, таблиця істинності для цього складного висловлювання буде складатися із чотирьох рядків. Якщо таблиця будується для простого висловлювання, то вона складатиметься із двох рядків відповідно до формули 21 = 2.

Побудуємо таблицю істинності для заперечення.

Слово "кон'юнкція" походить від conjnctio - зв'язок, сполучник.

У природній мові аналогами кон'юнкції є вирази "А разом з В", "А і В", "як А так і В", "А в той час як В", "В, хоча і А", "В, незважаючи на А", "не тільки А, а й В" і деякі інші.

У логіці кон'юнкцію позначають символами: "л".

Наведеному визначенню кон'юнкції відповідає така таблиця істинності:

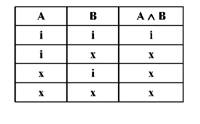
Відповідно до наведеної таблиці складне висловлювання "Ми знаходилися в аудиторії, і на вулиці йшов дощ" буде істинним лише тоді, коли істинними будуть обидва прості висловлювання "Ми знаходилися в аудиторії" і "На вулиці йшов дощ". В усіх інших випадках воно хибне.

Відомим фактом є багатозначність слів природної мови. І це стосується не тільки слів-іменників, а й сполучників, серед яких є і слово "або". Логіка створює спеціальні засоби, за допомогою яких аналізується подібна багатозначність і які дають можливість запобігти цій багатозначності.

Складне висловлювання, утворене за допомогою сполучника "або", відображає існування різних можливостей.

Наприклад, висловлювання "Він досяг гарних результатів у навчанні або завдяки старанності, або завдяки здібностям" відображає наявність різних можливостей отримання гарних результатів у навчанні. Це висловлювання буде істинним, якщо одна з двох можливостей реалізується. Істинним воно буде і тоді, коли реалізуються обидві можливості.

Таке висловлювання називають диз'юнктивним. Слово "диз'юнкція" походить від латинського disjnctio - роз'єднування, подія, розрізнення.

У природній мові аналогами диз'юнкції є вирази: "А або В", "А або В, або обидва", "А і або В", "А, якщо не В".

Для позначення диз'юнкції використовується символ: "/" . Різні значення сполучника "або" у логіці фіксуються:

- з'єднувальною диз'юнкцією (або просто диз'юнкцією), -розділовою диз'юнкцією (або суворою диз'юнкцією) і

- виключною диз'юнкцією (або анти кон'юнкцією). Прикладом з'єднувальної диз'юнкції є наведене тільки що висловлювання.

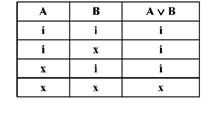
Отже, з'єднувальною диз'юнкцією називають складне висловлювання А V В, яке буде істинним тоді і тільки тоді, коли буде істинним хоча б одне з висловлювань А або В.

Наведення визначення відображене у таблиці істинності для диз'юнкції

Коли потрібно показати, що з двох можливостей реалізується тільки одна і що реалізація однієї можливості виключає реалізацію іншої, користуються розділовою, суворою або сильною диз'юнкцією.

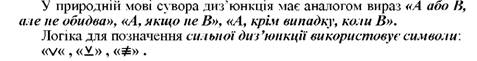
С и л ь н о ю диз'юнкцією називається висловлювання А v В, яке істинне тоді і тільки тоді, коли одне з простих висловлювань, що входять до його складу, істинне, а друге - обов'язково хибне.

Наприклад, "Ця людина або житель Києва, або іногородній". Таблиця істинності для сильної диз'юнкції має такий вигляд:

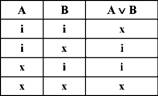
Сильною диз'юнкцією користуються тоді, коли відомо, що з двох можливостей, які включають одна одну, реалізуватися може лише одна, але невідомо яка саме.

Отже, у диз'юнкції істинність одного простого висловлювання не виключає істинності другого, а в сильній диз'юнкції істинність одного виключає істинність другого.

У природній мові сполучник "або" може вживатися і в третьому значенні, яке теж є виключаючим. Іноді нам необхідно сказати, що одна, а то й обидві можливості не мають місця.

Наприклад, у висловлюванні "Він є студентом або школярем" ми хочемо сказати, що він ні в якому випадку не є ні тим, ні іншим одночасно. В крайньому разі одним із них. За допомогою виразу "у крайньому разі" ми підкреслюємо, що він може бути ні тим, ні другим (стосовно нашого прикладу: він і не учень школи і не студент, а учень технікуму).

Тому наведене висловлювання буде істинним і тоді, коли обидва простих висловлювання хибні.

Таке складне висловлювання називають виключенням, або анти-кон'юнкцією. По суті, смисл сполучника "або" в цьому випадку можна передати комбінацією таких логічних термінів, як кон'юнкції і заперечення.

Комбінацію цих термінів позначимо вертикальною рискою (А | В). Складне висловлювання, яке виражає несумісність простих висловлювань, що його складають, називається виключенням або анти-кон'юнкцією.

Отже, виключенням (анти-кон'юнкцією) називають складне висловлювання, яке істинне тоді і тільки тоді, коли у крайньому разі одне з простих висловлювань, що його складають, хибне.

Цьому визначенню виключення відповідає таблиця істинності:

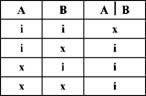
До багатозначних сполучників природної мови, крім сполучника "або", належить і сполучник "якщо, то", який фіксує той факт, що одне явище спричиняє інше. З'єднавши цим сполучником два прості висловлювання, отримаємо складне умовне висловлювання.

Граматичному сполучнику "якщо, то" відповідає логічний термін "імплікація". Слово "імплікація" походить від латинського implicite - тісно пов'язую.

Аналогами імплікації у природній мові є слова "якщо А, то В", "А тоді, коли В", "у випадку А, має місце В", "В, якщо А", "для В достатньо А", "для А необхідно В".

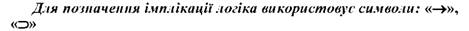
Однією з особливостей імплікації як логічного терміна, на відміну від уже розглянутих, є те, що прості висловлювання, поєднані імплікацією, не можна переставляти місцями, бо це змінить логічне значення складного висловлювання. Кожне з простих висловлювань, які входять до імплікативного висловлювання має спеціальну назву, відповідно до функцій, які воно виконує у складному висловлюванні.

Висловлювання, якому надіслане слово "якщо" і яке стоїть перед словом "то", називають антецедентом від латинського antecedens - попередній.

Висловлювання, яке стоїть після слова "то", називають консеквентом (з латинської consequens - наступний).

У літературі антецедент прийнято називати умовою, причиною, підставою, основою, а консеквент - наслідком, висновком.

Для імплікації характерна та обставина, що стверджуючи імплікацію, ми стверджуємо, що ні в якому разі не може трапитися так, щоб антецедент був істинним, а консеквент - хибним. Виходить, що імплікація істинна у трьох випадках:

- антецедент істинний і консеквент істинний;

- антецедент хибний, а косеквент істинний;

- антецедент хибний і консеквент хибний.

І лише коли антецедент істинний, а консеквент - хибний, імплікація - хибна.

Це відображено в таблиці істинності для імплікації:

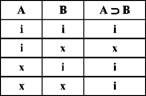
Звідси випливає, що приймаючи імплікацію за істинну і визначаючи істинним її антецедент, ми повинні визнати істинним і її консеквент, а приймаючи імплікацію за істинну і відкидаючи в то й же час її консеквент як хибний, ми повинні відкинути і її антецедент.

Для імплікації, як і для диз'юнкції, характерна багатозначність, що полягає у розбіжності між вживанням її у логіці і в побуті. Аналог імплікації у природній мові - сполучник "якщо, то" з'єднує два простих висловлювання у складне у тих випадках, коли між ними існує певний зв'язок за формою і змістом. Під цим зв'язком розуміється той факт, що консеквент обов'язково випливає з антецедента. Іншими словами, визнаючи антецедент за істинний, ми змушені визнати істинним і консеквент.

З чисто інтуїтивної точки зору можна сказати, що ми звертаємося до імплікації у наших міркуваннях тільки тоді, коли не впевнені, істинні її антецедент і консеквент чи ні. В усіх інших випадках вживання імплікації втрачає смисл.

Наприклад, "Якщо дане космічне тіло планета, то воно має природний супутник". Наведене висловлювання, як і будь-яке інше імплікативне висловлювання, містить певний сумнів, який кодується наведеною таблицею істинності.

А. Тарський у книжці "Вступ до логіки та методології дедуктивних наук" наводить один з фізичних законів ("Кожен метал є платичним"), який записує у вигляді імплікації: "Якщо х є метал, то х є пластичним". Ця імплікація є формою конкретних застосувань загального закону. Коли ми впевнені в істинності загального закону, то змушені визнати істинність усіх його часткових застосувань. Мається на увазі, що коли на місце х ми поставимо назву будь-якого матеріалу (наприклад, мідь, глина, камінь тощо), то завжди матимемо істинне конкретне імплікативне висловлювання. Можна легко переконатися, що:

а) всі висловлювання, отримані в результаті такої підстановки, відповідатимуть умовам істинності імплікації. Ми не матимемо ситуації, коли при істинності антецедента хибним буде консеквент;

б) у кожній з імплікацій як конкретизації загального закону існує тісний зв'язок між антецедентом і консеквентом, що відображається у формальному співпаданні їх суб'єктів;

в) приймаючи антецедент кожної з цих імплікацій (наприклад, "мідь - метал") за істинний, можемо вивести з нього істинний консеквент ("мідь - пластична"). Підставою для цього є загальний закон, що всі метали - пластичні.

Однак, як зазначає А.Тарський, з погляду природної мови деякі з імплікативних висловлювань будуть штучними і сумнівними.

Коли ми замість х підставим назву конкретного матеріалу, відносно якого ми не знаємо, чи є він металом і чи пластичний він, імплікативний зв'язок відповідатиме своєму призначенню. Якщо ми замінимо х "міддю", антецедент і консеквент будуть безсумнівно істинні. Тому тут доречніше замість імплікації вжити вираз: "Оскільки мідь - метал, то мідь - пластична". Підставивши замість х "глину", отримаємо імплікацію з хибним антецедентом і істинним консеквентом, яку доцільніше замінити виразом: "Хоча глина і не метал, вона - пластична". А дібравши для х назву такого матеріалу, коли утворена імплікація матиме хибним і антецедент, і консеквент, ми збережемо імплікацію, але при цьому необхідно змінити граматичну форму дієслів. Так, підставивши замість х "камінь", матимемо: "Як би камінь був металом, то він був би пластичним".

Враховуючи прагнення мови науки до суворого визначення термінів, логіка задає чітке визначення імплікації. Імплікація вважається осмисленою навіть тоді, коли між антецедентом і консеквентом немає ніякого зв'язку. Істинність чи хибність імплікації залежить виключно від істинності або хибності антецедента і консеквента.

Такий підхід дає можливість, по-перше, встановити логічний смисл виразу "якщо, то" і, по-друге, звільнити цей вираз від психологічних факторів. З цього погляду осмисленими будуть такі висловлювання:

Якщо Варшава - столиця Польщі, то Дніпро впадає в Чорне море. Якщо Варшава - столиця Франції, то Дніпро впадає в Чорне море. Якщо Варшава - столиця Польщі, то Дніпро впадає в Каспійське море. Якщо Варшава - столиця Франції, то Дніпро впадає в Каспійське море.

У природній мові ці висловлювання не мають смислу. Логіка ж визнає їх осмисленими, оскільки вони чітко фіксують логічне значення фрази "якщо, то", яке полягає в тому, що тільки третє висловлювання хибне, а решта - істинні. Імплікацію з таким визначенням називають матеріальною, тобто імплікацією, в якій між антецедентом і консеквентом немає змістовного зв'язку. Вперше концепцію матеріальної імплікації висунув давньогрецький філософ Філон (ІУст. до н.е.).

Крім матеріальної імплікації, існує і формальна.

Формальна імплікація - це вид імплікації, який фіксує змістовний зв'язок між антецедентом і консеквентом.

Назву "формальна" ця імплікація отримала завдяки тому, що антецедент і консеквент мають суб'єкти, які збігаються за формою. Прикладом може бути закон фізики, наведений А.Тарським "Для будь-якого х, якщо х є метал, то х є пластичний".

Б.Рассел запропонував застосовувати формальну імплікацію для позначення законів природи.

Отже, ми переконалися, що імплікація без смислового зв'язку між антецедентом і консеквентом звучить парадоксально. Незвичний вираз "Якщо пальми ростуть на полюсі, то крокодили літають" визнається істинною згідно з таблицею істинності для імплікації. Ця незвичність (ще раз підкреслимо) зумовлена тим, що в природній мові, користуючись імплікацією ми намагаємося передати певний смисловий зв'язок між антецедентом і консеквентом, а в логіці фіксується той факт, що імплікація хибна тільки при істинності антецедента і хибності консеквента.

Користуючись засобами природної мови, за допомогою сполучника "якщо, то" ми відображаємо різні смислові зв'язки між антецедентом і консеквентом. Ці зв'язки можуть бути таких видів:

а) причинний (наприклад, "Якщо через провідник пропустити електричний струм, то він збільшиться"). У цьому висловлюванні відображено те, що певна дія (пропуск електричного струму через провідник) є причиною збільшення провідника. При цьому перше повинно передувати другому;

б) зв'язок, який вказує, що знання про один факт є логічною підставою для ствердження знання про другий факт, (наприклад, "Якщо ртуть у термометрі піднялася, то в кімнаті стало тепліше"). Тут ми маємо справу вже не з причинним зв'язком, оскільки підйом ртуті у термометрі не спричиняє потепління в кімнаті;

в) зв'язок, який висуває один факт як умову для виникнення або існування іншого факту (наприклад, "Якщо я успішно складу сесію, то я поїду в закордонну мандрівку"). У цьому висловлюванні антецедент є обов'язковою умовою появи факту, що фіксує консеквент;

г) зв'язок, який відображає часову послідовність подій (наприклад, "Якщо сьогодні я закінчу писати статтю, то завтра віддам її на рецензію"). Це висловлювання фіксує часову (а не причинну) послідовність фактів, зафіксованих відповідно, в антецеденті і консеквенті.

Очевидно, що у кожному з цих висловлювань сполучник "якщо, то" має свою специфіку. У логіці ця специфіка відходить на другий план. Використовуючи імплікацію, ми, по суті, абстрагуємося від смислових відтінків сполучника "якщо, то", до яких звикли і які досить ефективно використовуємо в процесі спілкування. Цим ми досягаємо більшої точності в передачі інформації, але, зрозуміло, вимушені жертвувати змістом.

З наведених висловлювань можна зробити висновок, що будь-яке істинне умовне висловлювання фіксується істинною імплікацією, але не будь-яка істинна імплікація є виявом умовного висловлювання у звичайному смислі.

Охарактеризуємо природу наступного логічного терміна - еквіваленції.

Еквіваленція (або подвійна імплікація) висловлювань А і В - це складне висловлювання, яке буде істинним тоді і тоді, коли А і В одночасно істинні або одночасно хибні. В інших випадках еквіваленція буде хибною.

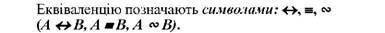
У природній мові аналогами еквіваленції є вирази: "А тоді і тільки тоді, коли В", "А якщо В і В якщо А", "Для А достатньо і необхідно В", "А матеріально еквівалентно В".

Наведеному визначенню еквіваленції відповідає така таблиця істинності:

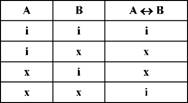
Ця таблиця відрізняється від таблиці істинності для імплікації третім рядком, а від таблиці істинності для конверсії імплікації - другим рядком.

Оскільки імплікація виражає відношення між достатньою умовою та її наслідком, а конверсія імплікації - між необхідною умовою та її наслідком, то еквіваленція або подвійна імплікація, виражає відношення між достатньою і необхідною умовою та її наслідком.

Наприклад, "Якщо він знає англійську мову, то він перекладе цей текст", "Якщо геометрична фігура квадрат, то її діагоналі діляться навпіл". Як у матеріальній імплікації сполучник "якщо, то ..." не виражає смислового зв'язку між антецедентом і консеквентом, так і в еквіваленції сполучник "якщо і тільки якщо" не виражає змістовно зв'язку між лівою і правою частинами еквівалентності; він виражає лише відношення між їх істинними значеннями ("істина", "хиба"). Ця особливість еквіваленції відіграє важливу роль для операцій із символами у логічних численнях.

Знання логічної еквіваленції дає можливість:

а) спростити запис послідовності висловлювань;

б) перейти від одного висловлювання до логічно еквівалентного йому (тобто, з тим самим істинним значенням);

в) замінити у послідовності формул одні формули на інші. Аналіз логічних зв'язок як однієї з підмножин множини логічних

термінів характеризує головні типи логічних відношень, без яких неможливо збагнути підвалини логіки висловлювань і логіки предикатів.

Окрім логічних зв'язок, серед логічних термінів виділяють логічні оператори, до яких відносяться квантори та описові вирази або оператори дескрипції.

Розрізняють два види кванторів:

- квантор загальності;

- квантор існування.

Слово "квантор" походить від латинського guantum - скільки. За допомогою кванторів виявляють відношення між предметною областю і предикатами, які визначені для неї.

Для позначення квантору загальності застосовують символи:

Наприклад, судження "Будь-яка планета є космічним тілом" можна записати , використовуючи квантор загальності у такому вигляді:

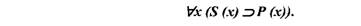
Читається вираз так: "Для будь-якого х, якщо х - планета, то х є космічним тілом". Такий запис свідчить, що це судження буде істинним для будь-якого х, визначеного на предметній області S, і хибним у протилежному випадку. Тобто, якщо ми на місце х поставимо назву будь-якої планети, отримаємо істинне судження. Саме цей факт фіксується формулою

Ось так можна охарактеризувати квантор загальності та квантор існування. Що ж стосується ще двох логічних операторів, а саме операторів дескрипції, то про них йдеться далі.

Розгляд логічних і дескриптивних термінів робить очевидним той факт, що логічні терміни фіксують ту сторону смислу висловлювання, яка виражає логічну форму відповідного судження. Щоб з'ясувати логічну форму судження і логічну структуру висловлювання, треба замінити всі дескриптивні терміни змінними символами відповідних категорій.

Наприклад, маємо висловлювання: "Будь-яка теорія має логічне обґрунтування". Випишемо дескриптивні терміни за допомогою символів: х, S, Р. І отримаємо вираз:

який представляє логічну форму даного висловлювання. А оскільки відомо, що процес отримання одних висловлювань з інших (що і є головним інтересом логіки) визначається їх логічною формою, то цю сторону смислу висловлювання називають його дедуктивним змістом.

Таким чином, головна функція логічних термінів - визначення дедуктивного змісту висловлювань.