Логіка - Конверський А.Є. - 1. Поняття функції

1. Поняття функції

Завершуючи розгляд питань, пов'язаних з логічним аналізом природної мови, зупинимося на визначенні поняття "пропозиційна функція".

Термін "пропозиційна функція" ввів в логіку Б.Рассел. Поняттю пропозиційна функція передує поняття функції в математиці. Відомо, що під функцією в математиці розуміють певний закон, за допомогою якого встановлюється відповідність між довільними об'єктами, одні з яких називаються значеннями аргументу, а інші - значеннями функції.

У логіці широко застосовується особлива функція - пропозиційна. Функціональному аналізу мови поклав початок 7". Фреге. Він показав, що низку мовних виразів можна тлумачити як деякі функції.

Застосування функціонального підходу в логіці зумовлене тим, що мова безпосередньо не виражає форми думки, лише аналізуючи спосіб буття, функціонування (вживання) відповідного мовного відрізка у структурі висловлювання, ми можемо сказати, носієм якої логічної форми він є.

Наприклад, поза структурою висловлювання не можна визначити, яку логічну форму втілює в собі слово "книга": чи це поняття, чи це предмет, чи це ознака.

У логіці виділяють функції власне логічні і предметні.

Серед логічних розрізняють пропозиційні функції і понятійні.

П р о п о з и ц і й н о ю або висловлювальною функцією є операція (дія), яка співвідносить предметам деякої предметної області значення істини або хиби.

Прикладами такої функції є вирази:

1. х - геніальний фізик;

2. х більше у.

х і у- предметні змінні, на місце яких ми можемо підставляти імена конкретних предметів із відповідних предметних областей.

Якщо взяти за предметну область множину людей (тобто вони можуть бути значеннями аргументу х), то підставивши у першу пропозиційну функцію замість х імена "Архімед", "Ньютон", отримаємо істину (значенням функції буде "істина"), а підставивши замість х імен "Платон", "Гегель" отримаємо хибу (значенням функції буде "хиба").

Якщо візьмемо за предметну область множину натуральних чисел, то пара чисел (3,1) перетворить другу функцію в істинне висловлювання, а пара чисел (1,2) - в хибне висловлювання.

За допомогою символів пропозиційну функцію записують у вигляді формул:

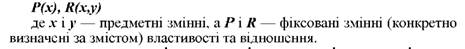
З точки зору функціонального підходу до логічного аналізу природної мови всі слова звичайної мови можна поділити на три групи:

а) слова, які можуть бути аргументами функцій (тобто слова, які можна підставляти замість змінних х, у ,z і т.д. у виразах Р (х), R(х,у,z), Q(у) і т.п.;

б) слова, що виконують роль пропозиційних функцій;

в) слова, які виконують роль логічних зв'язків і операцій (логічні постійні або логічні константи).

До слів, які можуть бути аргументами функцій, належать власні імена ("Варшава", "Арістотель", "Дніпро") і кількісні числівники ("два", "п'ять", "сім").

До слів, які виконують роль пропозиційних функцій належать іменники ("держава", "мати", "планета"), прикметники ("вчасний", "розчинний", "білий"), порядкові числівники ("другий", "п'ятий"), дієслова ("читає", "допомагає").

Здатність цих слів виконувати роль пропозиційних функцій зумовлена тим, що оперуючи ними, ми співвідносимо їх з індивідуумами із конкретних предметних областей, а результат такого співвідношення оцінюємо або як істинний, або як хибний. Іншими словами, за допомогою цих слів ми встановлюємо відповідність між предметами деякої предметної області і такими логічними об'єктами, як істина і хиба.

Враховуючи сказане, названі слова можна зобразити у вигляді таких виразів: "де - планета", "х - мати - у", "х - розчинний", "х - другий", "х - читає", "х - допомагає у" тощо (тобто ці слова виконують роль пропозиційних функцій з однією або кількома змінними).

І, нарешті, до слів, які виконують роль логічних зв'язків і операцій належать слова: "є", "якщо, то", "і", "або", "будь-який", "деякий", "неправильно" та ін.