Логіка - Конверський А.Є. - 10. Види складних суджень.

Дамо дефініцію с к л а д н о г о судження: "Складним судженням називається судження, яке складається із двох або більше простих суджень, з'єднаних відповідним логічним сполучником".

До складних відносяться:

1) з'єднувальні;

2) роз'єднувальні;

3) умовні;

4) рівнозначні або еквівалентні.

Розглянемо по черзі кожен із названих видів складних суджень.

До з'єднувальних суджень відносяться такі складні судження, які утворюються із двох або більше простих суджень, зв'язаних таким логічним сполучником, як кон'юнкція. Саме слово "conjunctio" є латинського походження і перекладається як з'єднання, зв'язок. В природній мові аналогами є слова: "і", "а", "але", "як тільки" та їм подібні. В логіці даний логічний сполучник позначається символами: " ^ ", "&", " o ".

Прикладом з'єднувального судження буде наступний вираз: "Мій брат - студент юридичного факультету, а сестра - студентка хімічного факультету".

Відомо, що структура простого судження представлена трьома складовими частинами: суб'єктом (S), предикатом (Р) і зв'язкою ("є" або "не є").

В пошуках структури складного судження ми приходимо до висновку, що основну, фундаментальну роль відіграє логічний сполучник. Саме завдяки логічній природі сполучника утворюється той чи інший вид складного судження. Прості судження, які входять до складного, виконують лише одну, єдину місію - "бути носієм логічного значення "істина" ("і") або "хиба" ("х")". Якщо прості судження до-

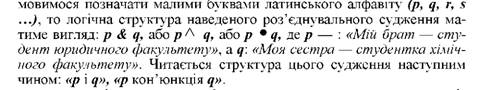
Отже, логічна структура з'єднувального судження складається із кон'юнкції (як логічного сполучника) множини конюнктів (у нашому випадку їх 2 - р і а).

Після виявлення логічної структури складного судження цілком слушно виникає питання про процедуру встановлення його значення. Якщо при встановленні значення для простого судження ми співставляли саме судження з тим, про що в ньому говориться, й істинне значення мало те судження, де між сказаним, проголошеним і наявним є відповідність, а хибне значення вказувало на відсутність відповідності сказаного і наявного, то при встановленні значення для складного судження має місце зовсім інша ситуація.

Значення складного судження передбачає не відповідність (чи невідповідність) сказаного і наявного, а впорядкованість значень простих суджень на основі відповідного логічного сполучника.

Зазвичай кажуть, що значення складного судження залежить від значень простих суджень, які його складають. Але ця залежність визначається природою логічного сполучника, завдяки якому утворюється складне судження.

Чисто технічно встановлення значення для складного судження здійснюється за допомогою таблиці істинності. Таблиця істинності будується за формулою: "2n =", де "2" - це кількість значень ("і", або "х"), які може мати просте судження, а "n" - це кількість простих суджень, що входять до складу складного судження.

Тоді, якщо наведене судження складається із двох простих суджень, то таблиця істинності для нього матиме 4 рядки: 22 = 4.

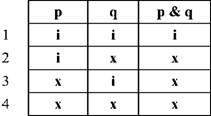
Дана таблиця показує, що кон'юнкція, як логічний сполучник, так впорядковує набори можливих значень для простих суджень, що лише 1-й рядок таблиці забезпечує значення істинності для з'єднувального судження. Іншими словами це означає, що скільки б простих суджень не входило до складу з'єднувального судження, воно буде істинним лише за умови 1-го рядка таблиці.

Отже, з'єднувальне судження (а або кон'юнкція)1 буде істинним лише тоді і тільки тоді, коли всі прості судження, які його складають, матимуть значення "істина". В решті випадків це судження буде хибним.

Характеризуючи складні судження загалом і, зокрема, з'єднувальне, слід звернути увагу ще на одну обставину. Коли ми говоримо, що логічні сполучники (кон'юнкція, диз'юнкція, імплікація, еквіваленція) мають своїми аналогами відповідні граматичні сполучники, то це означає, по-перше, що граматичні і логічні сполучники лише наближено схожі, а не взаємо замінювані; по-друге, граматичні сполучники зв'язують прості речення у складні за змістом, а логічні сполучники зв'язують прості судження у складні за значенням. Хоча часто буває, коли прості судження в складному відображають змістовний, смисловий зв'язок, як у наведеному вище прикладі, але це не є типовим для логіки.

Звісно, що в процесі обміну інформацією, в процесі спілкування ми вживаємо ті з'єднувальні судження, в яких між простими судженнями є смисловий, змістовний зв'язок. Проте це є винятком із загального правила. Тому з цих позицій істинними будуть судження: "Підозрюваний вчинив злочин, а потім він поніс покарання" і "Підписка про невиїзд - запобіжний захід, і Варшава - столиця Польщі".

В другому судженні відсутній змістовний зв'язок з позицій здорового глузду, але з точки зору логіки тут все гаразд: кон'юнкція (або з'єднувальне судження) істинна при будь-якій комбінації істинних простих суджень. Тобто, чи ми в складному судженні перше судження поставимо на місце другого, чи друге - на місце першого. Головне, щоб вони були істинні.

Цю обставину завжди потрібно мати в центрі уваги при аналізі складних суджень. Ще можна й так сказати: для логічного сполучника - кон'юнкції дозволена перестановка простих суджень місцями (тут діє закон комунікативності).

У той час як для граматичного сполучника "і" перестановка не завжди є коректною. Наприклад, якщо ми у вищенаведеному реченні, що містить думку про підозрюваного, який вчинив злочин і поніс покарання, поміняємо місцями прості речення, то отримаємо речення, яке не матиме смислового зв'язку, але судження, яке в ньому втілене, буде бездоганне з точки зору логіки: "Підозрюваний поніс покарання, а потім1 вчинив злочин". Така особливість складних суджень.

Другим видом складних суджень є роз'єднувальні судження.

Дамо дефініцію роз'єднувального судження: "Роз'єднувальним судженням називається судження, яке складається із двох і більше простих суджень, зв'язаних таким логічним сполучником, як диз'юнкція".

Слово "dicjunctio" латинського походження і перекладається як розділення, розрізнення. В природній мові аналогами диз'юнкції є слова "або", "чи" та їм подібні. В логіці диз'юнкція позначається символом " V ".

На відміну від кон'юнкції диз'юнкція має два значення: слабка диз'юнкція, або з'єднувально-роз'єднувальна диз'юнкція і сильна диз'юнкція, або сувора диз'юнкція.

Розглянемо ці види диз'юнкції по черзі. З'єднувально-роз'єднувальною диз'юнкцією називається логічний сполучник, який утворює роз'єднувальне судження із двох або більше простих і яке буде істинним при наявності в його складі істинного хоча б одного простого судження.

Звернемося до прикладу: "Переховуванням є приховання злочинця, або засобів скоєння злочину, або знарядь скоєння злочину, або слідів злочину, або предметів, здобутих злочинним шляхом".

Це судження ми називаємо з'єднувально-роз'єднувальним, тому що в ньому диз'юнкція вживається в послабленому значенні. Це означає, що наведене судження буде істинне і тоді, коли "переховування" виражатиметься лише у "прихованні злочину" і тоді, коли матиме місце одночасно і "переховування злочинця", "знарядь злочину", "предметів, здобутих злочинним шляхом".

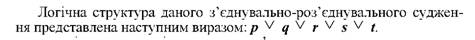
Прості судження, які входять до роз'єднувального судження, називаються альтернативними. Отже, в нашому судженні п'ять альтернатив.

Візьмемо для зручності приклад з'єднувально-роз'єднувального судження і побудуємо для нього таблицю істинності, тобто встановимо його значення.

Наприклад, "До Одеси із Києва можна доїхати поїздом, або автобусом". В наведеному судженні дві альтернативи: "До Одеси із Києва можна доїхати поїздом" - р, і "До Одеси із Києва можна доїхати автобусом" - q. Тоді за формулою "2n =" таблиця істинності для даного судження матиме 4 рядки:

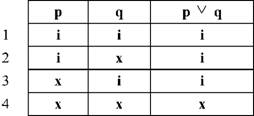
Отже, таблиця істинності для з'єднувально-роз'єднувального судження демонструє, що це судження буде хибним тоді і тільки тоді, коли жодна з альтернатив не реалізується, в решті випадків це судження буде істинним.

Звернемося до другого значення диз'юнкції, а саме - сильної диз'юнкції, або суворої диз'юнкції.

Дамо дефініцію сильної диз'юнкції: "Сильною диз'юнкцією називається диз'юнкція, яка із двох простих суджень утворює суворо-роз'єднувальне судження, яке буде істинним при реалізації лише однієї альтернативи і не реалізації іншої".

Наприклад, "Досудове слідство закінчується або припиненням справи, або відданням звинувачуваного в суд".

Побудуємо таблицю істинності для цього судження

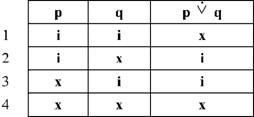
Другий і третій рядок таблиці показують, що в суворо роз'єднувальному судженні прості судження, що його складають, не можуть бути разом істинними і не можуть бути разом хибними. Якщо одне з них істинне, то це є підстава для визнання другого хибним і навпаки.

Наступним видом складного судження є умовне судження. Умовним судженням називається таке складне судження, яке складається із двох простих суджень, з'єднаних таким логічним сполучником, як імплікація.

Слово "implicatio" є латинського походження і перекладається, як тісно зв'язувати. В природній мові цей сполучник має аналогом слова: "якщо, то". В логіці даний сполучник позначають символами:

Структура умовного судження складається із імплікації, підстави або причини, або основи) і наслідку.

Опишемо структуру умовного судження. Судження, яке стоїть до знаку імплікації, називається підставою, або основою, або умовою, або латинською мовою - антецедентом. Антецедент перекладається як попередній.

Судження, яке стоїть після знаку імплікації, називається наслідком, або висловом, або результатом, або латинською мовою - консеквентом. Консеквент перекладається як наступний.

Після цих пояснень структуру умовного судження можна представити як комбінацію антецедента, імплікації і консеквентна.

Характеризуючи логічну структуру умовного судження, слід звернути увагу на такі обставини:

- по-перше, в умовному судженні не можна переставляти місцями судження, які його складають (тобто міняти місцями умову і наслідок) без зміни значення вихідного судження;

- і, по-друге, умовне судження найбільш рельєфно, випукло показує, що в складних судженнях прості судження зв'язуються логічними сполучниками за значенням, а не за змістом.

Стосовно першої обставини звернемося до прикладу про свідка, який ми наводили вище. Якщо судження "Якщо він свідок, то він повинен говорити правду" є безсумнівно істинне, то утворене від нього: "Якщо він говорить правду, то він свідок" таким не є. Людина може бути не свідком і говорити правду і навпаки.

Для пояснення другої обставини візьмемо судження, які очевидно є хибними і жодним чином не пов'язані за змістом та з'єднаємо їх імплікацією: "Якщо Аристотель автор Римського права, то Наполеон автор "Руської правди"". І перше речення, і друге - хибні і не зв'язані за змістом, але в цілому це судження має значення - "істина". Іншими словами, в цьому судженні мається на увазі інший, прихований смисловий відтінок, який ми хочемо в такий спосіб посили: "Якщо невірно, що Аристотель написав Римське право, то тим більш невірно, що Наполеон є автором "Руської правди"".

Після визначення логічної структури умовного судження встановимо його значення за допомогою таблиці істинності:

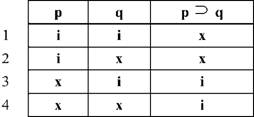
В таблиці істинності видно, що умовне судження буде хибним лише в 2-му рядку таблиці, коли умова (або анцедент) - істинна, а наслідок (або консеквент) - хибний. В решті випадків умовне судження буде істинним.

Описуючи структуру умовного судження, ми виділяли судження, яке стоїть до знаку імплікації як підставу. У зв'язку з цим виникає потреба вказати види підстав і дати їх визначення.

Існує три види підстав: "достатня підстава", "необхідна підстава", "достатня і необхідна підстава".

Дамо визначення кожної з підстав. Достатньою підставою називається підстава, при наявності якої наслідок наступає, а при її відсутності наслідок може як наступити, так і не наступити.

Прикладом достатньої підстави в судженні: "Якщо він свідок, то він повинен говорити правду" є факт того, що дана особа згідно процесуальному кодексу визнана свідком.

А якщо людина не є свідком, то вона може говорити правду, а може - ні. Тобто, наслідок може наступити, а може - ні. Про це свідчить 3 і 4 рядки наведеної вище таблиці істинності для імплікації.

Отже, дана підстава є достатня, але не необхідна.

Необхідною підставою є підстава, відсутність якої викликає відсутність наслідку, а при її наявності наслідок як може наступити, так і не наступити.

Для прикладу візьмемо судження: "Якщо він народний депутат, то його можуть обрати Головою Комітету Верховної Ради України". Відсутність ознаки народного депутата викликає відсутність можливості займати посаду Голови Комітету Верховної Ради України. а наявність цієї ознаки ще не означає, що цього депутата оберуть Головою Комітету Верховної Ради України, тому що крім посвідчення депутата потрібно володіти ще рядом ознак - фахових, етичних, ділових і т.д. Отже, ця підстава є необхідна, але не достатня.

Наступним складним судженням є рівнозначне судження або еквівалентне.

Визначимо дане судження: "Рівнозначним або еквівалентним судженням називається таке складне судження, яке складається із двох простих, з'єднаних таким логічним сполучником, як еквіваленція".

прикладом еквівалентного судження є вираз: "Якщо і тільки якщо рішення суду справедливе, то воно достатньо обґрунтоване". Структуру цього судження можна записати наступним чином: р "

Визначимо значення рівнозначного судження за таблицею істинності:

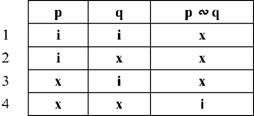
З таблиці істинності видно, що рівнозначне судження буде істинним, коли обидва прості судження, що його складають, будуть мати однакові значення (разом істинні, або разом хибні), в решті випадків воно буде хибним.

Еквіваленцію іноді називають подвійною імплікацією, або прямою і зворотною імплікацією. Це пояснюється тим, що істинність рівнозначного судження передбачає рівні значення суджень, що його складають. Дана обставина дозволяє нам ввести крім розглянутих вище достатньої підстави і необхідної підстави ще один від підстави, а саме - достатню і необхідну підставу.

Достатньою і необхідною підставою є підстава, при наявності якої наслідок наступає, а при її відсутності наслідок не наступає.

В нашому прикладі "справедливе рішення суду" є і достатньою і необхідною підставою. Або в судженні "Якщо і тільки якщо він знає англійську мову, то він перекладе цей текст" знання англійської мови є достатньою підставою (наслідок наступить, текст буде перекладено за умови знання англійської мови) і в той же час є і необхідною підставою (наслідок не наступить, текст не буде перекладено без знання англійської мови).

Охарактеризовані вище логічні сполучники, завдяки яким утворюються розглянуті види складних суджень, називаються бінарними або подвійними. Тобто для їх застосування потрібні хоча б два простих судження. Але є ще один логічний сполучник, який можна застосовувати до одного судження - це заперечення.

Запереченням називається логічна дія, за допомогою якої істинне судження перетворюється в хибне, а хибне - в істинне.

В природній мові заперечення передається словами "ні", "невірно", "не може бути" і їм подібними. В логіці заперечення записується символами: "-", "1", "~".

Таблиця істинності, оскільки заперечення можна застосовувати до одного судження, матиме два рядки:

Маємо істинне судження: "Будь-який свідок повинен говорити правду". Здійснимо його заперечення: "Невірно, що всі свідки повинні говорити правду".

Отже, ми отримали із істинного судження хибне судження.

Ми розглянули окремо кожен логічний сполучник і наочно переконалися, яку логічну дію кожен з них вчиняє. Також була продемонстрована особливість складних суджень порівняно з простими в процесі побудови міркувань.