Логіка - Конверський А.Є. - 3. Висновки із категоричних суджень

Розглянемо умовиводи, для аналізу яких недостатньо засобів логіки суджень, а необхідно враховувати внутрішню структуру засновків і висновку.

Отже, йтиметься про силогістику Арістотеля, яка викладена у славнозвісних "Аналітиках".

Висновки із категоричних висловлювань поділяються на:

- безпосередні та

- опосередковані.

а) Безпосередні умовиводи.

До безпосередніх умовиводів відносять:

а) обернення, перетворення, протиставлення предикату;

б) умовиводи за логічним квадратом.

До опосередкованих умовиводів відносять простий категоричний силогізм.

Б е з п о с е р е д н і м умовиводом називається дедуктивний умовивід, у якому висновок отримують із одного засновку.

У практиці міркувань зустрічається той факт, що побудова різноманітних умовиводів дозволяє виділити і донести до співрозмовника смислові відтінки інформації, що міститься в засновках. Особливо це очевидно у випадку з безпосередніми умовиводами:

Всі студенти історичного факультету вивчають логіку - (засновок)

1. Отже, деякі особи, що вивчають логіку є студентами історичного факультету - (висновок, отриманий шляхом обернення засновку).

2. Жоден студент історичного факультету не може бути серед тих, хто не вивчає логіку - (висновок, отриманий шляхом перетворення засновку)._

3. Жоден, хто не вивчає логіку не належить до студентів історичного факультету - (висновок, отриманий, шляхом протиставлення предиката засновку до суб'єкта)._

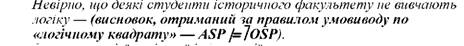
Отримання тієї чи іншої інформації з конкретного висловлювання обумовлюється безпосередньою мовною ситуацією (це може бути урок, бесіда, будь-яке пояснення тощо), дослідницькими мотивами, суто практичними міркуваннями. Про це і свідчать наведені приклади.

Обернення.

Аналіз безпосередніх умовиводів розпочнемо з обернення.

Якщо взяти категоричне судження, то в ньому безпосередньо наявна інформація про відношення S до Р і є прихованою інформація про відношення Р до S. Саме тому, метою безпосереднього умовиводу шляхом обернення є отримання інформації про відношення Р до S у структурі категоричного судження.

Схема цього умовиводу така:

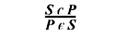
Отже, о б е р н е н н я м називається такий безпосередній умовивід у висновку якого суб'єктом стає предикат засновку, а предикатом - суб'єкт засновку.

У процесі отримання умовиводу шляхом обернення відбувається перестановка місцями S і Р, але якість засновку зберігається для висновку. У ролі засновків можуть виступати судження А, Е, І, О.

Якщо у ролі засновку маємо судження А, то у висновку отримуємо судження І:

Всі підручники мають методичний зміст.

Отже, деякі книги методичного характеру є підручниками.

Зауважимо, що в безпосередніх умовиводах шляхом обернення, перетворення, протиставлення предиката діють правила розподіленості термінів у категоричних судженнях.

Якщо у ролі засновку наявне судження Е, то у висновку також отримуємо судження Е:

Жодний мій знайомий не був учасником минулого кінофестивалю.

Отже, жоден учасник минулого кінофестивалю не був серед моїх знайомих.

У випадку із судженням І висновком матимемо судження І:

Деякі книги нашої бібліотеки є рідкісними. Отже, деякі рідкісні книги є в нашій бібліотеці.

Відповідно до загальних правил про розподіленість термінів у засновку і висновку судження О оберненню не підлягає. Наприклад, "Деякі рослини не є деревами" - із цього судження шляхом обернення неможливо отримати істинний висновок.

Обернення суджень Е і І називають оберненням без обмежень. Обернення судження А називають оберненням з обмеженням.

Перетворення.

Розглянемо умовиводи, які отримують у результаті перетворення засновку.

Схемою такого умовиводу є:

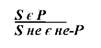
Виявляється, що в категоричному судженні, окрім явного знання про відношення Р до S (про що йшлося вище), міститься неявне знання про відношення S до Р.

Наприклад, якщо всі елементи множини S належать множині Р (у випадку судження А), то ні в якому разу вони не можуть належати множині Р (доповненню Р).

В умовиводі шляхом п е р е т в о р е н н я м и отримуємо висновок де суб'єктом є суб'єкт засновку, а предикатом є поняття, що суперечить предикату засновку. Це стає можливим завдяки зміні якості засновку.

Тобто, здійснюється це шляхом введення у висновок двох заперечень одного перед зв'язкою, а іншого - перед предикатом.

У ролі засновків виступають судження А, І, Е, О. Отже, існують чотири варіанти перетворення.

Судження А перетворюється у судження Е.

Наприклад,

Усі мої друзі мають вищу освіту._

Отже, серед моїх друзів немає жодного, хто не мав би вищої освіти.

Схематично це можна зобразити так:

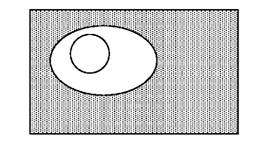
Отже, якщо всі елементи множини S належать множині Р, то ні в якому разі вони не можуть належати множині не-Р (доповненню Р).

Судження Е перетворюється у судження А.

Зауважимо, що вставляючи у судженні Е, як у засновку, заперечення перед зв'язкою, отримуємо подвійне заперечення. Тому ми їх усуваємо керуючись принципом: подвійне заперечення рівносильне твердженню.

Наприклад,

Жоден мій приятель не має вищої освіти.

Отже, усі мої приятелі є людьми без вищої освіти.

Схема цього умовиводу така:

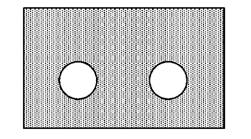
Наведена схема показує, що усі елементи множини S належать множині не-Р.

Судження І перетворюється у судження О.

Наприклад,

Деякі мої приятелі вивчають англійську мову. Отже, деякі мої приятелі не належать до людей, що не вивчають англійську мову.

Схема цього умовиводу така:

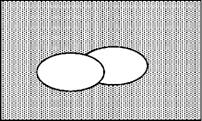
Ця схема показує, що частина S (заштрихована) не належить множині не-Р.

Судження О перетворюється в судження І.

Наприклад,

Деякі науки не є гуманітарними. Отже, деякі науки є не гуманітарними

Схематично цей умовивід зображується так:

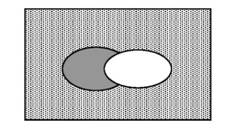
Схема вказує на те, що частина множини S (заштрихована) належить множині не-Р.

У процесі отримання умовиводу шляхом перетворення необхідно відновити зв'язку, яка часто опускається у засновку і, лише потім, послідовно ввести заперечення перед зв'язкою та предикатом у висновку.

Протиставлення предикату.

Вказуючи на те, що із відношення S до Р можна отримати інформацію про відношення S до Р, необхідно враховувати ще один вид інформації, що випливає з цього відношення, тобто йдеться про відношення Р до S.

Таке перетворення категоричного судження (у ролі засновку) називається безпосереднім умовиводом через протиставлення предикату. Схема цього умовиводу така:

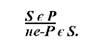
Протиставленням предикату називається такий безпосередній умовивід у результаті якого отримують висновок суб'єктом якого є поняття, що суперечить предикату засновку, а предикатом стає суб'єкт засновку.

Протиставлення предикату розглядається як результат двох послідовних дій: перетворення і обернення.

Наприклад,

Будь-яка наукова теорія об'єктивно відображає дійсність. І Отже, жодна наукова теорія не може не об'єктивно відображати дісність.

II. Отже, все, що не об'єктивно відображає дійсність не може належати до наукової теорії.

Із судження А шляхом протиставлення предикату отримують судження Е.

Наприклад,

Будь-яка теорія підтверджується на практиці. Отже, все, що не підтверджується на практиці не теорією.

Схематично цей умовивід зображується так:

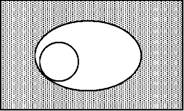
Наведена схема демонструє, що множини не-Р і S не мають жодного спільного елементу.

Із судження Е шляхом протиставлення предикату отримують судження А.

Наприклад,

Жоден мій приятель не має вищої освіти. Отже, деякі люди без вищої освіти мої приятелі.

Схема цього умовиводу така:

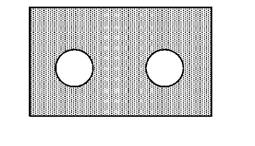
Із цієї схеми очевидно, що лише деякі елементи множини не-Р є спільними з елементами множини S.

Із судження О шляхом протиставлення предикату отримують судження І.

Наприклад,

Деякі студенти не є учасниками конференції. Отже, деякі не учасники конференції студенти.

Схематично це зображується так:

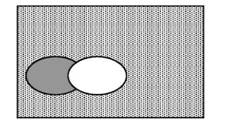
Ця схема вказує на те, що лише частина елементів не-Р і S є спільними.

Із судження І шляхом протиставлення предикату висновок отримати неможливо. Це зумовлено тим, що перетворюючи судження /, отримують судження О, яке оберненню не підлягає.

Умовиводи за "логічним квадратом".

Будувати безпосередні умовиводи можна не лише із урахуванням інформації між 5 і Р, але й виходячи із змісту логічних відношень між категоричними судженнями. Нагадаємо, що таких відношень існує чотири види: підпорядкування, суперечності, противності і підпротивності.

Умовиводи, які будуються із урахуванням цих 4-х типів відношень між категоричними судженнями, називають умовиводами за "логічним квадратом".

Побудова умовиводів за "логічним квадратом" підпорядкована певним правилам, які:

по-перше, забезпечують правильність умовиводу в кожному конкретному випадку; а

по-друге, дають систематичний огляд всіх можливих міркувань такого типу.

Правила висновку умовиводів за "логічним квадратом" поділяються на:

- основні та

- похідні.

Розпочнемо аналіз цих правил з основних.

До основних правил висновку відносяться правила, які регламентують умовиводи, що засновані на:

а) відношенні контрадикторності, або суперечності, і

б) підпорядкування.

Зазначимо, що при побудові умовиводів за "логічним квадратом" використовуються, окрім суджень ASP, ESP, ISP, OSP ще й одиничні судження: а єР та а єР.

Якщо засновоком буде будь-яке із 6 категоричних висловлювань: ASP, ESP, ISP, OSP а є P, а є P, то можна побудувати правильні умовиводи на основі вказаних правил.

Коректність похідних правил можна перевірити, побудувавши їх доведення:

Таким способом можна довести всі похідні правила.

Розглядаючи умовиводи "за логічним квадратом", ми переконалися, що суттєвою особливістю безпосередніх умовиводів є отримання інформації різноманітних відтінків.