Логіка - Конверський А.Є. - г) Умовиводи логіки висловлювань в традиційній логіці.

Окрім розглянутих правил висновку логіки висловлювань у традиційній логіці досліджується низка умовиводів логіки суджень на аналізі яких ми зупинимося.

Традиційна логіка розглядає умовиводи логіки висловлювань, засновками яких є комбінації категоричного судження з умовним чи розділовим судженням, комбінації тільки умовних суджень і комбінації з умовних і розділових суджень. Зокрема, це такі :

1) умовно-категоричні умовиводи;

2) чисто умовні умовиводи;

3) розділово-категоричні умовиводи;

4) умовно-розділові умовиводи.

Охарактеризуємо кожний із цих видів умовиводів.

У м о в н о - к а т е г о р и ч н и м називається умовивід, у якому один засновок умовне судження, а другий засновок і висновок категоричні судження.

Існує два різновиди умовно-категоричного умовиводу:

- modus ponens і

- modus tollens.

Розглянемо "modus ponens" .

У перекладі з латинської мови "modus ponens означає "від ствердження підстави до ствердження наслідку".

Наприклад,

Якщо гіпотеза підтверджується на практиці, то вона стає теорією. Дана гіпотеза підтверджується практикою. Отже, вона перетворюється в теорію.

Мовою логіки висловлювань структуру цього міркування можна записати у вигляді правила висновку:

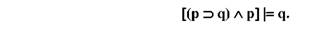
Дане правило широко використовується у сучасній логіці. Справа в тому, що умовивід "від ствердження підстави до ствердження наслідку" є зручним засобом пошуку доведення для довільної думки. Виявляється, що для того, щоб довести висловлювання q необхідно знайти висловлювання р, яке б не тільки було істинним, а й складена із р та

У перекладі з латинської мови означає "від заперечення наслідку до заперечення підстави".

Наприклад,

Якщо у діях підозрюваного є ознаки складу злочину, то порушується кримінальна справа.

Кримінальна справа стосовно громадянина N не порушена. Отже, в діях громадянина N немає ознак складу злочину.

Структуру цього умовиводу можна записати у вигляді правила висновку

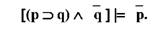
Щоб відрізнити правильні умовно-категоричні умовиводи від неправильних потрібно співставити структуру конкретного умовиводу із структурами стверджувального і заперечувального модусів умовно-категоричних умовиводів:

Даний вираз не співпадає ні з формулою і , ні з формулою 2. Отже, цей умовивід є неправильним.

Ч и с т о у м о в н и м називається умовивід у якому засновки і висновок є умовними судженнями.

Наприклад,

Якщо студент здібний, то він має досягнення у науковій роботі. Якщо студент має досягнення у науковій роботі, то його можна рекомендувати до вступу в аспірантуру.

Отже, якщо студент здібний, то його можна рекомендувати до вступу в аспірантуру.

Логічну структуру цього умовиводу представляє така формула:

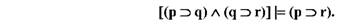
У логіці висловлювань ця формула є правилом висновку, яке називається "транзитивністю імплікації":

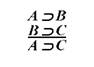
У практиці міркувань широко застосовується розділово-категоричний умовивід.

Р о з д і л о в о - к а т е г о р и ч н и м умовиводом називається умовивід у якому один засновок розділове судження, а другий засновок і висновок категоричні судження.

Наприклад,

До Києва із Одеси можна доїхати потягом або автобусом.

До Києва із Одеси не можна доїхати автобусом._

Отже, до Києва з Одеси можна доїхати потягом.

Розділово-категоричний силогізм має два правильних різновиди:

- "modus tollendo ponens" і

- "modus ponendo tollens". "Modus tollendo ponens".

У перекладі з латинської мови означає "заперечувально-стверджуючий модус".

Очевидно, що тут диз'юнкція береться у з'єднувально-розділовому смислі.

Перевіримо правильність цього умовиводу, побудувавши для виразу, що представляє його логічну структуру аналітичну таблицю:

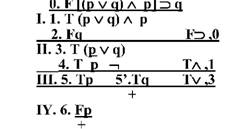
Аналітична таблиця замкнена отже, даний вираз представляє логічно коректне правило умовиводу. Перевіримо чи буде правильним у цьому випадку хід міркування від ствердження до заперечення.

Аналітична таблиця не замкнена. А це означає, що умовивід, логічна структура якого представлена даною формулою, є неправильним. Треба мати на увазі, що в заперечувально-стверджуючому розділово-категоричному умовиводі диз'юнкція вживається у з'єднувально-розділовому смислі.

"Modus ponendo tollens"

Другим правильним різновидом розділово-категоричного умовиводу є стверджувально-заперечувальний модус, або латинською мовою "modus ponendo tollens".

При побудові розділово-категоричних умовиводів необхідно дотримуватися таких правил:

1. У стверджувально-заперечувальному модусі1 більший засновок має сполучник "або", який вживається у строго розділовому смислі.

2. У більшому засновку повинні бути перераховані усі альтернативи2. Якщо цього не зробити, то отримаємо хибний засновок, а це означає, що такий умовивід буде не ефективним.

Наприклад,

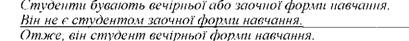
Наступним видом у класі умовиводів логіки суджень є умовно-розділові умовиводи.

Ум о в н о -р о з д і л о в и м умовиводом називається умовивід, у якому один із засновків є розділовим судженням, а решта умовними судженнями.

Наприклад,

Якщо ранкові газети повідомлять про результати референдуму, то я ще сьогодні зможу підготуватися до виступу. Якщо вечірні газети повідомлять про результати референдуму, то я лише завтра зможу підготуватися до виступу. Результати референдуму повідомлять або ранкові, або вечірні газети.

Отже, я зможу підготуватися до виступу або сьогодні, або завтра.

Умовно-розділові умовиводи мають ще одну назву - лематичні. Ця назва походить від грецького слова lemma - припущення. Така назва зумовлена тим, що вона випливає з тієї характеристики умовиводів, що розглядають різні припущення та їх наслідки.

В залежності від кількості альтернатив у розділовому засновку лематичні умовиводи поділяють на:

а) дилеми (дві альтернативи);

б) трилеми (три альтернативи);

в) полілеми (чотири і більше альтернатив).

У практиці міркувань найчастіше використовують дилеми, тому зупинимося на їх аналізі.

За якістю наслідку (заперечувальний або стверджувальний) дилеми поділяють на:

- конструктивні та

- деструктивні.

За складністю наслідку дилеми поділяють на:

- прості та

- складні.

К о н с т р у к т и в н о ю називається дилема у висновок якої входять наслідки умовних засновків.

Д е с т р у к т и в н о ю називається дилема, висновок якої складається із заперечення підстав умовних засновків.

П р о с т о ю називається дилема, висновком якої є наслідок умовного засновку, або заперечення підстави умовного засновку.

С к л а д н о ю називається дилема, висновком якої є диз'юнкція наслідків умовних засновків або заперечення підстав умовних засновків.

Наведемо приклади. І. Якщо в діях підозрюваного є ознаки шахрайства, то проти нього може бути порушена кримінальна справа. Якщо в діях підозрюваного є ознаки крадіжки, то проти нього може бути порушена кримінальна справа. В діях підозрюваного можуть бути ознаки шахрайства або крадіжки. Отже, проти підозрюваного може бути порушена кримінальна справа.

Маємо просту конструктивну дилему (ПКД):

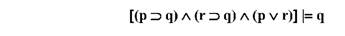
Якщо N вчинив протиправні дії, то N понесе матеріальні збитки.

Якщо N вчинив протиправні дії, то N понесе моральні збитки.

N не понесе ні матеріальних, ні моральних збитків. Отже, він не вчиняв протиправних дій.

Такий вигляд має проста деструктивна дилема (ПДД):

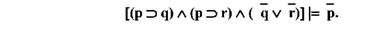
III. Якщо іспит вступний, то він може впливати на конкурс. Якщо іспит семестровий, то він може впливати на отримання стипендії.

Іспити бувають вступні або семестрові.

Отже, іспити можуть впливати або на конкурс, або на отримання стипендії.

У складній конструктивній дилемі (СКД) висновком є складне диз'юнктивне судження, альтернативами у якому є наслідки умовних засновків:

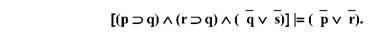
Отже, складна конструктивна дилема є слабким ствердженням яких-небудь суджень (точніше їх диз'юнкції), а складна деструктивна дилема використовується для слабкого їх заперечення. Іншими словами, якщо неможливо прямо довести хибність якого-небудь судження р

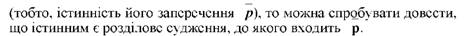
Якщо мати на увазі наведену вище типологію правил висновку логіки висловлювань, то схеми висновку за простою та складною конструктивною дилемами належатимуть до похідних прямих правил:

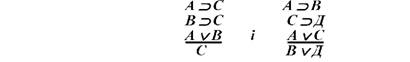
Стосовно схем висновку простої та складної деструктивної дилем, то їх відносять до похідних непрямих правил:

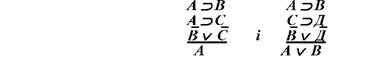
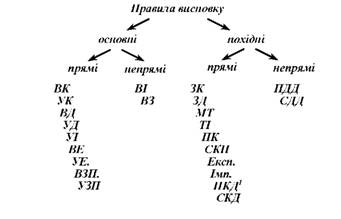
Нарешті, після розгляду умовних, умовно-категоричних, розділово-категоричних та умовно-розділових умовиводів логічні структури яких є відповідними правилами висновку можна повністю відтворити схему типології правил висновку логіки висловлювань.