Умовивід аналізується на двох рівнях: синтаксичному і семантичному.
З точки зору синтаксису умовивід являє собою правило висновку. Правилом висновку є норма, що дозволяє із суджень однієї логічної структури як засновків отримувати судження певної логічної структури як висновок.
Кожне правило репрезентує нескінченну множину умовиводів різноманітних за змістом, але єдиної синтаксичної структури.


Ця логічна структура є правилом висновку, яке регламентує найрізноманітніші міркування лише в рамках схеми, заданої цим правилом.

Враховуючи характеристику правила висновку, наведеного вище, можна сказати, що систематичний огляд правил висновку логіки суджень сприятиме розгляду всіх можливих міркувань у цій логіці. Тому розглядаючи те чи інше правило висновку логіки суджень, мають на увазі, що тут йдеться про конкретні міркування, які репрезентуються цим правилом.
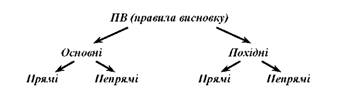
Правила висновку логіки висловлювань поділяються на:
- основні та
- похідні.
У свою чергу основні та похідні правила поділяються на:
- прямі та
- непрямі.
О с н о в н и м и називаються правила, які змістовно очевидні і дозволяють відрізнити правильно побудовані міркування від неправильно побудованих міркувань.
П о х і д н и м и називаються правила, які виводяться із основних і сприяють скороченню процесу висновку.
П р я м и м и називаються правила, які вказують на безпосереднє виведення висновку із засновків.
Н е п р я м и м и називаються правила, які дають можливість стверджувати правомірність деяких висновків на основі визнання правомірності інших висновків.
Систему правил висновку логіки суджень можна записати за допомогою такої схеми:
Розгляд правил висновку логіки суджень розпочнемо з основних прямих правил.
Правило введення кон'юнкції (ВК):
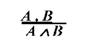



Правило введення диз'юнкції (ВД):


Треба враховувати різницю смислів сполучника "або": і) сполучно-розділове "або"; і) суворо розділове "або".
Нехтування цією різницею при вживанні диз'юнкції призводить до логічної помилки. Наприклад,

Якщо приєднати висновок до засновків через імплікацію, то у результаті не отримаємо тотожно-істинної формули, а отже, висновок не відповідає визначенню правильного дедуктивного умовиводу.
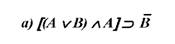
У тих випадках, коли неможливо вирішити, в якому смислі вживається сполучник "або", треба посилатися на смисл сполучника "або" у сполучно-розділовому розумінні.
Розглянемо другий приклад.
Правила висновку логіки висловлювань бувають основні та похідні.
Це правило - основне_
Отже, це правило не похідне.
Логічна структура цього міркування має такий вигляд:


Приклад міркування за правилом введення еквіваленції:
Якщо суд визнає вину обвинувачуваного, то він мав на це достатні підстави.
Якщо суд має достатні підстави щодо визнання вини обвинувачуваного, то він визнає його винним.
Отже, якщо і тільки якщо суд визнав вину обвинувачуваного, то він мав на це достатні підстави.


Як уже зазначалося, окрім наведених основних прямих правил висновку логіки висловлювань існують і основні непрямі. До них відносяться:
а) правило введення імплікації,
б) правило введення заперечення.
Розглянемо правило введення імплікації: Правило введення імплікації (ВІ):

Це правило використовується у тих вивідних процесах, коли для отримання висновку ми звертаємося до припущень, які полегшують процедуру виведення. Його можна сформулювати так: "Якщо із засновків П і з припущення А випливає В, то можна стверджувати вивідність із цих засновків А ^В".

І. Якщо в діях обвинувачуваного не має складу злочину,
то суд його виправдає.
Суд визнав обвинувачуваного винним.
В діях обвинувачуваного немає складу злочину.
Суд визнав обвинувачуваного невинним.
Отже, невірно, що в діях обвинувачуваного
немає складу злочину.
II. Якщо в діях підозрюваного є склад злочину, то проти нього може бути порушена кримінальна справа. Якщо проти підозрюваного порушена кримінальна справа, то лише суд визначає міру запобіжного заходу. Отже, якщо в діях підозрюваного є склад злочину, то лише суд може визначити міру запобіжного заходу.
Визначення цього правила таке: "Якщо із засновків і довільного припущення А випливають два суперечливих висловлювання В і В, то таке припущення повинно бути визнаним як хибне, істинним визнається А".
Зупинимося на розгляді похідних правил висновку логіки висловлювань.
Правило транзитивності імплікації (ТІ) :

в) Метод аналітичних таблиць.
г) Умовиводи логіки висловлювань в традиційній логіці.
3. Висновки із категоричних суджень
а) Безпосередні умовиводи.
б) Простий категоричний силогізм.
в) Перевірка коректності силогізму.
г) Ентимема.
д) Силогістика та метод аналітичних таблиць.
4. Недедуктивні умовиводи