Логіка - Конверський А.Є. - б) Простий категоричний силогізм.

Уперше систематичний розгляд теорії висновку дає Арістотель в "Аналітиках", вона отримала назву "силогістика".

К а т е г о р и ч н и м с и л о г і з м о м називають дедуктивний умовивід, який складається із двох засновків і висновку, представлених судженнями виду: ASP, ESP, ISP, OSP.

Іншими словами, простий категоричний силогізм це такий дедуктивний умовивід в якому висновок здійснюється із двох категоричних суджень на основі співвідношення дескриптивних термінів.

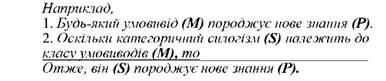
Аналізуючи наведений приклад категоричного силогізму, стає очевидним, що він за структурою складається із трьох термінів: S, М, Р.

Термін, що входить до висновку як його суб'єкт називається м е н ш и м і позначається буквою S.

Термін, який виконує роль предиката висновку називається б і л ь ш и м і позначається буквою Р.

Більший і менший терміни називаються к р а й н і м и.

Термін, що входить в обидва засновки, але відсутній у висновку, називається с ер е д н і м і позначається буквою М.

У відповідності до назви термінів засновок, до якого входить більший термін, називається більшим.

Засновок, до якого входить менший термін, називається меншим.

У нашому прикладі більший засновок 1, а менший - 2. Виходячи із зазначеного, структуру силогізму можна записати у вигляді імплікації, де антецедентом буде кон'юнкція засновків, а консеквентом - висновок:

Ці схеми називають фігурами категоричного силогізму, тобто різновидами категоричного силогізму, які визначаються розташуванням середнього терміна.

Різновиди категоричного силогізму розрізняють за формами засновків і висновку. їх прийнято називати модусами категоричного силогізму.

При побудові категоричного силогізму дотримуються певних правил, які поділяються на:

а) загальні правила категоричного силогізму і

б) спеціальні правила фігур.

До загальних правил категоричного силогізму відносяться такі:

1. У простому категоричному силогізмі повинно бути лише три терміни.

2. Середній термін повинен бути розподіленим хоча б в одному з засновків.

3. Якщо крайній термін розподілений (або не розподілений) у засновку, то він повинен бути розподіленим (або не розподіленим) у висновку.

4. Якщо один із засновків заперечувальне судження, то і висновок буде заперечувальним судженням.

5. Якщо один із засновків часткове судження, то і висновок буде частковим судженням.

6. Із двох заперечувальних суджень висновок отримати не можливо.

7. Із двох часткових суджень висновок отримати неможливо.

Спеціальні правила фігур Перша фігура:

1. Більший засновок - судження загальне.

2. Менший засновок - судження стверджувальне.

Друга фігура:

1. Більший засновок повинен бути загальним судженням.

2. Один із засновків заперечувальне судження.

Третя фігура:

1. Менший засновок - стверджувальне судження.

2. Висновок - часткове судження.

Четверта фігура:

1. Якщо більший засновок стверджувальне судження, то менший повинен бути загальним судженням.

2. Якщо один із засновків заперечувальне судження, то більший засновок повинен бути загальним судженням.

Побудуємо доведення спеціальних правил.

Спеціальні правила фігур виводяться із загальних, а також із знання про розташування середнього терміна в засновках. Прикладом може служити доведення правил першої фігури.

Припустимо, що правила першої фігури неправильні, а правильні їх заперечення:

1. Більший засновок повинен бути частковим судженням.

2. Менший - заперечувальним судженням.

Якщо у результаті доведення цього припущення прийдемо до суперечності, то наше припущення відпаде як хибне, а істинними визнається твердження, що складає правила першої фігури.

Доведення:

- якщо приймаємо наше припущення, то висновком у силогізмі за першою фігурою буде заперечувальне судження (4 - загальне правило силогізму: скорочено - ЗПС);

- окрім цього, висновок буде частково-заперечувальним судженням OSP (по 5 - ЗСП);

- у заперечувальному судженні Р - розподілений:

- отже, більший термін буде розподілений і у засновку (3 - ЗСП);

- оскільки більший і менший засновки заперечувальні, то висновок отримати неможливо (6 - ЗПС).

Таким чином, наше припущення невірне і воно відпадає. Тоді коректними будуть названі правила першої фігури. Таким способом доводять правила решти трьох фігур.

Використовуючи ЗПС і спеціальні правила фігур, для кожної фігури можна вивести усі правильні модуси. У межах кожної фігури можливі 16 комбінацій засновків від чотирьох видів суджень ASP,

ESP, ISP, OSP:

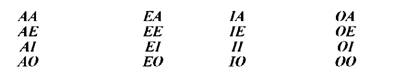
Перше правило виключає повністю комбінації 3 і 4 колонок. Варіанти 2 і 4 першої колонки суперечать першому правилу фігури.

Варіанти 2 і 4 другої колонки виключаються з розгляду за 6 - ЗПС.

Отже, залишаються комбінації АА, АІ, ЕА, ЕІ із яких отримують модуси AAA, All, ЕАЕ, ЕІО. Кожний модус має конкретне ім'я, що використовується як певний мнемонічний засіб: Barbara, Celarent, Darii, Ferio .

Таким же чином можна вивести правильні модуси П, Ш, ІУ фігур. Із чотирьох фігур перша вважається найдосконалішою. Це зумовлено такими обставинами:

По-перше, тільки ця фігура дає у висновку всі чотири типи категоричних суджень.

По-друге, в першій фігурі частковий випадок підводиться під загальне положення.

По-третє, тільки ця фігура дає у висновку висловлювання ASP, мовою якого формулюються закони науки.

Зважаючи на це модуси першої фігури приймаються як основні, а модуси решти трьох фігур як похідні, які можна вивести із основних.

Спочатку обґрунтуємо коректність модусів першої фігури, а потім перейдемо до виведення модусів П, Ш, ІУ фігур.

Логічна коректність модусів першої фігури випливає із умов істинності суджень ASP, ESP, ISP, OSP.

Візьмемо модус AAA.

Спочатку припустимо, що засновки AMP і ASM - істинні, а висновок - ASP - хибний. Потім, відповідно до умови істинності загально стверджувального судження: якщо ^4SP - хибне, то у множині S знайдеться хоча б один індивід а, який не належить множині Р. Але за угодою, якщо ASM - істинне, то будь-який індивід множини S належить множині М (навіть і а). Однак, одночасна приналежність а до класу М і не приналежність до класу Р виключається в силу угоди про істинність засновку AMP. Тобто, все, що належить М (а М належить і індивід а) належить і Р. Таким чином, наше припущення про істинність AMP і ASM та хибність висновку ASP приводить до суперечності, чим і встановлюється логічна коректність модусу AAA.

Обґрунтуємо модус ЕАЕ.

Знову припускаємо, що засновки ЕМР і ASM - істинні, а висновок ESP - хибний. Якщо ESP - хибне, то за умовою істинності загальнозапечувального судження, існує хоча б один індивід а множини S, який належить множині Р. За припущенням висновок ASM - істинний, отже, кожен індивід із S, в тому числі і а належить М. Але приналежність предмета а множині Р і множині М виключається припущенням про істинність засновку ЕМР. Виходить, що припущення про істинність ЕМР і ASM та хибність ESP спростоване і цим самим визнається логічна коректність модусу ЕАЕ.

Обґрунтуємо коректність третього модусу першої фігури АП.

Припустимо, що засновки AMP і ISM - істинні, а висновок ISP - хибний. Відповідно до умов істинності частковостверджувального судження, якщо засновок ISM - істинний, то існує в крайньому разі, один індивід а множини S, який належить і множині М. У той же час за умови хибності висновку ISP не існує жодного індивіда множини S, тому числі і індивіда а, який би не належав множині Р. Належність а множині М і неналежність а множині Р суперечить припущенню про істинність засновку AMP. Адже AMP істинне, якщо всі елементи множини М (в тому числі і а) належать множині Р. Отже, припущення про істинність засновків AMP і ISM та хибність висновку ISP відпадає. Цим самим стверджується логічна коректність модусу All.

Нарешті побудуємо доведення для четвертого модусу першої фігури ЕIO.

Нехай засновки ЕМР і ISM - істинні, а висновок OSP - хибний. За умови істинності частковостверджувального судження ISM істинне, коли , у крайньому разі, існує хоча б один індивід а множини S, який належить М. Висновок OSP хибний (за умов істинності частково-заперечувального судження), коли всі індивіди множини S, в тому числі і а, який належить М, належать Р. Однак, належність індивіда а множині М і множині Р суперечить умовам істинності загальнозапе-речувального судження, яким представлений більший засновок і який, згідно припущення є істинним. Отже, припущення про істинність засновків ЕМР і ISM, та хибність висновку OSP спростовується і цим доводиться логічна коректність модусу АІО.

Таким чином, використовуючи умови істинності ASP, ESP, ISP та OSP обґрунтовують логічну коректність модусів першої фігури.

Логічна коректність модусів II, III та ІУ фігур встановлюється за допомогою модусів першої фігури та відповідних правил висновку.

Зауважимо, що назви модусів (особливо П, Ш, та ІУ фігур) виконують не тільки мнемонічну функцію. Початкові букви В, С, О, F вказують на ті модуси першої фігури, які отримують в результаті зведення. Голосні вказують на кількісну і якісну характеристики засновків та висновку конкретного модусу, а приголосні на спосіб його обґрунтування:

- буква s показує, що судження, яке позначене голосною, після якої стоїть ця буква, повинно піддаватися чистому оберненню;

- буква p означає, що судження, яке позначене голосною, після якого стоїть ця буква, повинне піддаватися оберненню з обмеженням;

- буква m вказує на заміну місцями засновків;

- буква c вказує, що даний модус може бути зведеним до модусу першої фігури шляхом непрямого доведення..

Візьмемо модус "Cesare". Буква С вказує на те, що його можна звести до модусу "Celarent". Буква s вимагає при зведенні обернути більший засновок без обмеження:

Наведені доведення модусів свідчать про те, що зазначений вище список правил висновку достатній для обґрунтування логічної коректності будь-якого модусу II, III та ІУ фігур.