Менеджмент организаций - Киржнер Л.А. - 6. МОДЕЛИ И МЕТОДЫ ПРИНЯТИЯ РЕШЕНИЙ

6.1. Сущность моделирования. Классификация моделей

Одним из исследовательских видов человеческой деятельности является моделирование, т. е. способ изучения закономерностей изменения структуры экономических процессов или явлений под воздействием различных факторов. В основе моделирования лежит понятие о модели.

Модель — один из важнейших инструментов научного познания, условный образ объекта исследования (или управления). Модель конструируется субъектом исследования (или управления) так, чтобы отобразить характеристики объекта (свойства, взаимосвязи, структурные и функциональные параметры и т.п.), существенные для целей исследования. Поэтому вопрос о качестве такого отображения — адекватности модели объекту — правомерно решать лишь относительно определенной цели. Модель — искусственно созданный объект, который будучи адекватным исследуемому объекту, отображает и воспроизводит в более простом виде структуру, связи и взаимосвязи между элементами исследуемого объекта, непосредственное изучение которого связано с какими-либо трудностями, и тем самым облегчает процесс получения информации об интересующем нас объекте. Следовательно, практическое значение модель может иметь при условии, что ее анализ (путем активного эксперимента, дедуктивного исследования и т.д.) более доступен субъекту исследования в соответствии с имеющимися у него средствами, чем непосредственное изучение объекта.

Конструирование модели на основе предварительного изучения объекта и выделение его существенных характеристик, экспериментальный и (или) теоретический анализ модели, сопоставление результатов с данными об объекте, корректировка модели и т.д. составляют содержание моделирования.

Предпосылкой относительно большей доступности модели для анализа в сравнении с объектом является то, что моделирование, как правило, приводит к упрощенному образу объекта (исключение могут составлять случаи, когда одна абстрактная система рассматривается как модель другой, тоже абстрактной системы).

Существует множество определений и классификаций моделей применительно к задачам разных наук. Наиболее строгое и общее из них опирается на понятия гомоморфизма и изоморфизма. Образ объекта исследования, который формируется у наблюдателя в соответствии с его целью, является гомоморфным — упрощенным, поскольку абстрагирование, отвлечение от несущественных, с точки зрения данной цели, свойств объекта, является необходимым условием всякого исследования. Далее наблюдатель строит собственно модель: абстрактную или материальную систему, изоморфную сформированному ранее упрощенному образу относительно набора фиксированных свойств (или отношений).

Более формально: из двух систем М1 и М2 каждая является моделью другой, если существует такой гомоморфный N1 системы М1 и такой гомоморфный образ N2 системы М2, которые изоморфны между собой.

Кроме того, при построении модели необходимо выполнять требования рефлексивности (т.е. любая система есть своя собственная модель), симметричности (любая система есть модель своей модели, т.е. оригинал и модель могут меняться "ролями") и транзитивности (т.е. модель модели есть модель исходной системы). И, наконец, последнее свойство: поскольку модель является целевым отображением, то отсюда следует множественность моделей одного и того же объекта: для разных целей обычно требуются разные модели.

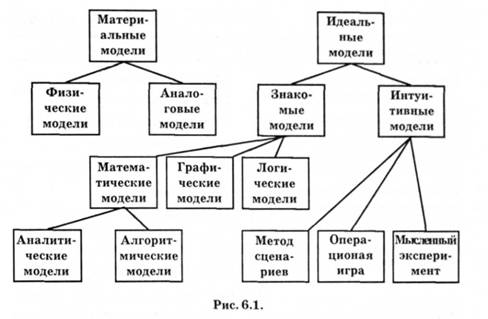
Существует множество классификаций моделей, например рис. 6.1, и соответственно методов моделирования. Так, в зависимости от деления целей на теоретические и практические модели делятся на познавательные и прагматические. Познавательные модели являются формой организации и представления знаний, средством соединения новых знаний с имеющимися. Прагматические модели являются средством управления, средством организации практических действий, способом представления образцово-правильных действий или их результата.

Модель называется абстрактной (концептуальной), либо материальной (физической) в зависимости от того, какой системой она является, т.е. от выбора средств моделирования. Абстрактной моделью может быть, в частности, система математических выражений, описывающих характеристики объекта моделирования и взаимосвязи между ними (математическая модель). Модели с конкретными числовыми значениями характеристик называют числовыми моделями, модели, записанные с помощью логических выражений, — логическими моделями, модели в графических образах — графическими моделями (графики, диаграммы, рисунки). К логическим моделям обычно относят блок-схемы алгоритмов и программы расчетов. В зависимости от типа вычислительных машин, на которых осуществляется моделирование, различают аналоговые и дискретные (цифровые) модели. Их основой является математическая модель в широком значении этого термина. Вместе с тем аналоговые модели могут рассматриваться и как материальные, поскольку в конечном счете они основаны на получении физического образа исследуемого процесса. Большое распространение имеют и такие материальные модели, как уменьшенные макеты, действующие модели различных приборов и устройств, тренажеры и т.п. Модель может отражать внутреннюю структуру объекта и воспроизводить отношения между его элементами, таковы, например, системы моделей композиционного планирования. В других случаях, когда внутренняя структура объекта недоступна исследователю, модель отражает лишь его поведение или функционирование, определяя зависимости между воздействиями на объект и его состояние. Модели, при построении которых преследуется цель определения такого состояния объекта, которое является наилучшим в каком-либо смысле или допустимым с точки зрения субъекта моделирования, называются нормативными, модели, предназначенные для объяснения наблюдаемых фактов или прогноза поведения объекта, называются дескриптивными. Иначе говоря, нормативные модели отвечают на вопрос "Как должно быть", дескриптивные — на вопросы "Как это происходит?", "Как это будет развиваться?".

Модели должны обладать следующими свойствами: полнотой, точностью, правильностью. Эти характеристики объединяет понятие адекватности. Модель, с помощью которой успешно достигается поставленная цель, называется адекватной этой цели. Адекватность означает, что требования полноты, точности и правильности выполнены не вообще, а лишь в той мере, которая достаточна для достижения цели.

Как и все в мире, модели имеют свой жизненный цикл: они возникают, развиваются, сотрудничают или соперничают с другими моделями, затем уступают место более совершенным. В этом проявляется динамика модели.

Экономическая наука давно использует модели. Эффективность применения моделей определяется также научной обоснованностью их предпосылок, умением исследователя выделить существенные характеристики объекта моделирования.

Экономико-математические модели базируются также на понятиях изоморфизма и гомоморфизма. Поэтому существует два уровня типологии экономико-математических моделей, на каждом из которых в соответствии с определенными основаниями классификации выделяют различные группы моделей (табл. 6.1).

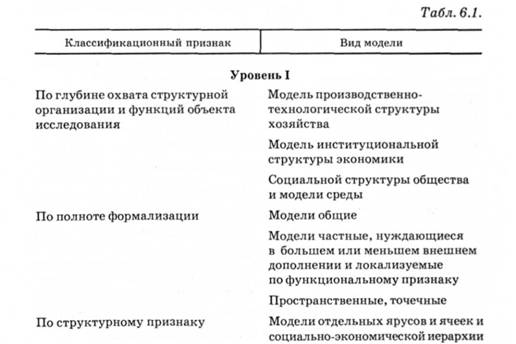
Приведенная выше классификация видов моделей не охватывает всего многообразия моделей. Ее можно проводить по различным основаниям, по характеру моделируемых объектов, по сферам приложения моделирования и его уровням.

Следует также учитывать, что модели проходят свой жизненный цикл: они возникают, развиваются, сотрудничают или соперничают с другими моделями, уступают место более совершенным. В этом проявляется динамика модели.