Менеджмент организаций - Киржнер Л.А. - 6.2. Построение модели

Рассмотрим основные этапы построения модели принятия решений. При этом следует учитывать, что прежде чем приступить к количественному анализу проблемы принятия управляющего решения, необходим ее тщательный качественный анализ. Цель та* кого анализа заключается в выявлении тех факторов, которые являются наиболее важными, необходимо также составить предварительное представление содержательной стороны управляющих решений о критериях оценки эффективности различных вариантов решений, а также о той схеме оценки и сравнения различных критериев, которая может быть использована при сравнении возможных альтернатив. При этом необходимо заранее учитывать, как относятся к рассматриваемой задаче руководители, занимающие ответственные посты и располагающие полномочиями принимать управляющие решения.

Первый этап. Постановка задачи. В результате предварительного диагностического анализа должны быть определены основные элементы проблемы. В частности, необходимо указать управляемые переменные (т.е. переменные, значения которых задаются управляющим решением), неуправляемые переменные, а также ограничения, которым подчиняются переменные по условию задачи. Кроме того, следует сформировать целевую установку проблемы, т.е. вложить конкретное содержание в требования по совершенствованию управляющего решения.

Формулируя задачу, следует установить пределы возможностей анализа.

Задачи организационного управления, как правило, таковы, что результаты их решения проявляются многократно. Одни из них приводят к определенному эффекту немедленно, последствия же других (возможно, в равной степени важные) проявляются лишь спустя некоторое время. При определении границ применимости анализа по тому или иному признаку следует руководствоваться достаточным практическим опытом и здравым смыслом.

Второй этап. Построение математической модели. На этом этапе необходимо определить надлежащие входные данные и дать общее представление о соответствующем информационном выходе. Следует также провести различие между статистическими и динамическими структурными элементами задачи и попытаться представить в математической форме взаимосвязи между этими элементами. Некоторые из взаимозависимостей между теми или иными параметрами задачи можно записать в виде алгебраических соотношений, другие допускают вероятностную интерпретацию. Следует также установить "временной горизонт", т.е. интервал времени, в течение которого должны проявляться следствия организационно-управленческого решения. Это позволит произвести оценку принятых критериев эффективности различных возможных вариантов решений.

В самом общем виде модель может быть представлена следующим образом:

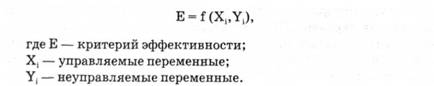
Ограничения, наложенные на переменные, могут быть выражены в дополнительной системе равенств или неравенств.

Третий этап. Нахождение решения с помощью модели. Существует два метода получения оптимального решения (или некоторого приближения к нему) с помощью модели: аналитический и численный. Аналитические процедуры сводятся к использованию математической дедукции. Это требует использования различных разделов математики, таких, как математический анализ и матричная алгебра. Аналитические решения получаются в абстрактном виде, т.е. подстановка чисел вместо символов обычно производится уже после того, как будет получено решение.

Численные процедуры состоят в принципе в подборе различных значений для управления переменных моделей, сопоставлении полученных данных и выборе того набора значений, который дает наиболее выгодное решение. Такие процедуры могут варьироваться в широком диапазоне от простого метода проб и ошибок до сложных итераций. Процедура итераций состоит в том, что в результате последовательных итераций производится попытка подойти к оптимальному решению. Кроме того, итерация обычно дает некоторый набор правил, которые позволяют опознать оптимальное решение, когда оно найдено.

Некоторые выражения в модели не могут быть численно определены с достаточной точностью вследствие каких-либо математических или чисто практических причин. Во многих подобных случаях для получения примерной оценки предложений может быть применен особый вид случайных выборок, называемый методом Монте-Карло.

Четвертый этап. Проверка модели и решения. Модель всегда лишь частично отображает действительность. Модель можно считать хорошей, если, несмотря на свою неполноту, она может точно предсказывать влияние изменений в системе на общую эффективность всей системы. Адекватность модели может быть проверена путем определения степени точности предсказания влияния этих изменений. Решение может быть оценено путем сопоставления результатов, полученных без использования данного решения, и результатов, полученных при его применении. Эти оценки могут производиться ретроспективно с использованием ранее полученных данных или путем практических испытаний и предварительных проверок. Проверка требует очень тщательного анализа данных с целью определения, какие из них являются существенными и какие нет.

Пятый этап. Построение процедуры подстройки решения. Решение, полученное на модели, действительно только до тех пор, пока неуправляемые переменные сохраняют свои значения и соотношения между переменными в модели остаются постоянными. Когда же значение одной или более неуправляемых переменных либо одно или более отношений между переменными существенно изменилось, само решение "выходит из-под контроля" и возможность управления им теряется. Существенность изменения зависит от того, насколько решение отклоняется от истинного оптимизма при изменившихся условиях, установить процедуру подстройки решения, необходимо разработать средства определения того, когда возникают существенные изменения; кроме того, должны быть установлены правила такой модификации решения, которая бы учитывала эти изменения.

Шестой этап. Осуществление решения. Проверенное решение должно быть представлено в виде ряда рабочих процедур, которые могут быть легко поняты и применены теми, кто будет отвечать за их осуществление. При этом должны быть определены и соблюдены необходимые изменения в существующих процедурах и ресурсах. Перечисленные этапы почти никогда, за редкими исключениями, не проводятся в указанном порядке. Более того, некоторые из этих этапов могут осуществляться одновременно. Например, во многих операционных проектах формулирование задачи продолжается фактически вплоть до завершения всего исследования. В процессе исследования, как правило, различные направления работы непрерывно взаимодействуют друг с другом.