У психології часто використовують різні числа. Змінні, які є результатами замірів, називають варіантами (вони варіюються, тобто змінюються) і їх позначають Хі Усі значення змінної, які розташовані в одному ряду у порядку зростання або зменшення, утворюють варіаційний ряд. Кількість повторень однакових результатів у складі варіаційного ряду називається частотою цього значення змінної.
Нормальний розподіл даних. Одиничний розподіл даних як стандарт.
Для того, щоб від розподілу випадкових подій перейти до кривої нормального розподілу, необхідно зробити лише один крок. Нормальна крива — це частотний розподіл подій, коли кількість їх дуже велика.
Для вибіркових даних формула підібраної нормальної кривої виглядає так:

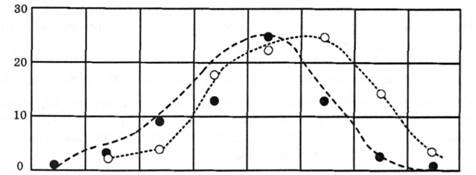
Розглянемо на прикладі вирівнювання емпіричних варіаційних кривих за нормальним законом Муавра, Лапласа, Гауса. Досліджували вибірку ( N = 90) працівників на визначення рівня інтелектуального розвитку (табл. 5.5; табл. 5.6; табл 5.7).
Табулювання даних: ранговий порядок, розподіл частот.
Таблиця 5.5. Результати досліджень рівня інтелектуального розвитку працівників-регулювальників кольорових телевізорів
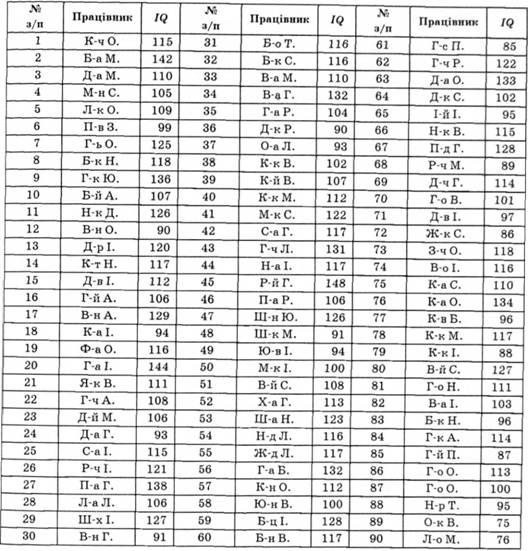
Таблиця 5.6. Складання варіаційного ряду первинних даних

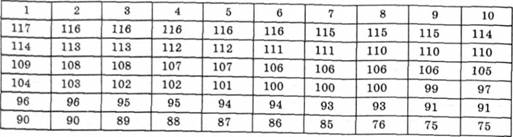
Таблиця 5.7. Групування класів
| Дати | Кількість класів |
| 6—11 | 4 |
| 12—22 | 5 |
| 23—46 | 6 |
| 47—93 | 7 |
| 94—187 | 8 |
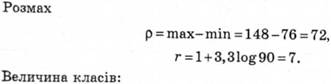

Таблиця 6.8. Вирівнювання емпіричної варіаційної кривої за нормальним законом
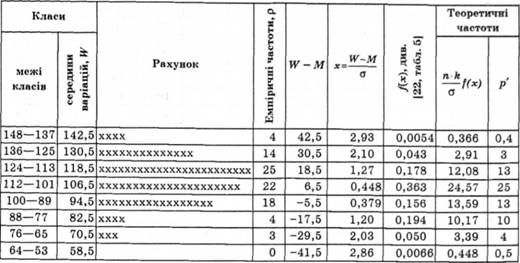
Алгоритм вирівнювання емпіричних варіаційних кривих за нормальним законом Гауса-Лапласа (рис. 5.1):

Таблиця 5.9. Співвідношення різних типів шкал оцінювання
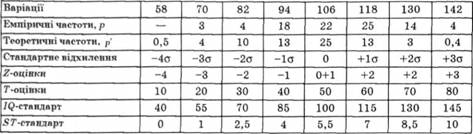
Середнє арифметичне (середнє значення або вибіркове середнє) дорівнює сумі всіх значень варіанти, поділеній на кількість членів варіаційного ряду (n). Його визначають за формулою:
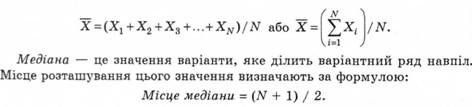
Мода — значення варіаційного ряду, яке трапляється найчастіше.
Перелічені три величини є мірами центральної тенденції і їх використовують залежно від характеру розподілу значень досліджуваної змінної і завдань, що стоять перед діагностом.
Для оцінки зміни значень змінної використовують такі характеристики, як дисперсія і середньоквадратичне (або стандартне відхилення).
Дисперсія дорівнює квадрату середніх відхилень значення варіанти від середнього значення. Вона є однією з характеристик індивідуальних результатів розкиду значень досліджуваної змінної біля середнього значення.
Значення дисперсії використовують у різних статистичних розрахунках, але не має безпосереднього спостережливого характеру. Величиною, яка безпосередньо пов'язана зі змістом змінної, що спостерігається, є середньоквадратичне відхилення. Воно дорівнює квадратному кореню з дисперсії і визначається за формулою:
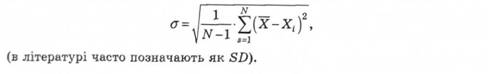
Стандартне відхилення широко використовують як міру розкиду для різних характеристик.
Побудова гикали за даними експерименту.
Для того щоб надати експериментальним даним наочну форму, часто треба подати їх в одній із шкал оцінювання. Розглянемо таку процедуру на прикладі.
Припустимо, що Ви провели обстеження 65 працівників за допомогою тесту інтелекту й отримали такі результати (в балах):
| 59 | 48 | 53 | 47 | 57 | 64 | 62 | 62 | 65 | 57 | 57 |
| 81 | 83 | 48 | 65 | 76 | 53 | 61 | 60 | |||
| 37 | 51 | 51 | 63 | 81 | 60 | 77 | 71 | 57 | 82 | 66 |
| 54 | 47 | 61 | 76 | 50 | 57 | 58 | 52 | |||
| 57 | 40 | 53 | 66 | 71 | 61 | 61 | 55 | 73 | 50 | 70 |
| 59 | 50 | 59 | 83 | 69 | 66 | 67 | 47 | |||
| 56 | 60 | 43 | 54 | 47 | 81 | 76 | 69 |

Таблиця 5.10. Шкала інтервалів
| №з/п | Межі інтервалів | Кількість осіб, які потрапили в цей інтервал |
| 01 | 86—40 | 2 |
| 02 | 41—45 | 1 |
| 08 | 46—50 | 9 |
| 04 | 51—55 | 9 |
| 05 | 56—60 | 13 |
| 06 | 61 — 65 | 10 |
| 07 | 66—70 | 7 |
| 08 | 71—75 | 3 |
| 09 | 76—80 | 4 |
| 10 | 81—85 | 6 |
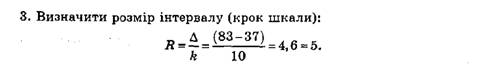
4. Побудувати інтервали шкали.
5. Побудувати гістограму (рис. 5.2).
Побудувавши шкалу і подавши результати експерименту на гістограмі, ми можемо зробити якісний аналіз даних тесту. В нашому прикладі розподіл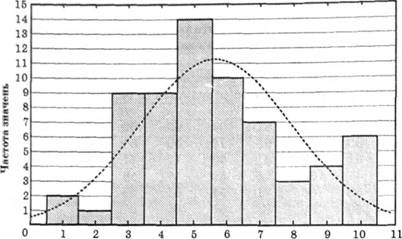
Класи
Рис. 5.2. Крива побудови розподілу емпіричних даних
даних значно відрізняється від нормального розподілу. Це зумовлено двома причинами:
1) поганий тест;
2) опитування проведено на нерепрезентативній вибірці (є дві підгрупи обстежуваних: із середніми та високими показниками інтелекту).
Підбір суб'єктів дослідження.
Для визначення об'єму вибірки за допомогою математичної формули треба хоча б приблизно знати величину середнього квадратичного відхилення (о*) ознаки, яку вивчають.
Помилка вибіркового дослідження зменшується зі збільшенням вибірки. Ця залежність є в основі вирішення "зворотного" завдання — скільки треба взяти людей або провести дослідження, щоб можна було гарантувати достовірний результат.
Сформульоване завдання розв'язують за допомогою формули:
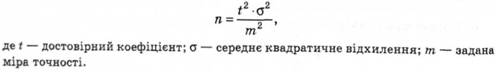
Послідовність операцій при використанні згаданої формули ми покажемо на типовому прикладі.
Припустимо, що вимагають визначити кількість досліджень, потрібних для отримання достовірних результатів показників успішності навчання
молодого працівника двома різними методами пошуку пошкоджень у радіоапаратурі — цілісним методом і частинами.
Прийнято, що в психологічних дослідженнях мінімальною припустимою достовірною ймовірністю є 95 %, тобто тільки в п'яти випадках зі ста можуть виникнути показники, які не підтверджують прийняту гіпотезу. Такій імовірності відповідає коефіцієнт достовірності t = 1,96 ≈ 2.
Припустимо, що за умовами завдання дослідження можна скористатися величиною стандартного квадратичного відхилення, яку отримали в аналогічних попередніх експериментах, і воно становитиме 1.1. Вважатимемо, що для розв'язання поставленого завдання в експерименті буде потрібна міра точності в 0,2 бала. Іншими словами, коливання середньої величини оцінки успішності не повинні перевищувати 0,2 бала.
Знайдені значення підставляють у формулу:
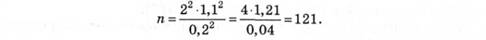
Отже, надійність результатів дослідження можна досягнути тільки при об'ємі матеріалу, який дорівнює мінімум 121 показнику. В цьому випадку його можна отримати лише за рахунок кількості досліджуваних (121 особа).
Теорія статистичного висновку (статистична перевірка наукової гіпотези ).
Без підготовки в галузі теорії і методів перевірки статистичних гіпотез неможливо читати наукові звіти й розуміти їх. Теорія статистичного висновку — це формалізована система методів виконання завдань через виведення властивостей великого масиву (генеральної сукупності) даних шляхом обстеження вибірки. Завдання полягає в тому, щоб передбачити властивості всієї сукупності, знаючи лише властивості вибірки із цієї сукупності.
Які висновки можна зробити про властивості генеральної сукупності за вибірковим спостереженням?
Є два види гіпотез: наукові та статистичні. Наукова гіпотеза — це запропоноване розв'язання проблеми. Це розумно обґрунтоване й розвинуте допущення. Його перевіряють результатами експерименту, які відповідають на запитання: буде гіпотеза істиною чи ні. Статистична гіпотеза — просто судження стосовно невідомого параметра. Статистичною називають гіпотезу про вид невідомого розподілу або про параметри відомих розподілів. Статистичною називають гіпотезу про те, що змінна в генеральній сукупності розподілена за нормальним законом. Гіпотезу, що перевіряють, називають нульовою і позначають Н0. Поряд з нульовою розглядають конкуруючу (альтернативну) гіпотезу H1 яка її заперечує.
Статистичні критерії. Для перевірки Н0 використовують спеціально підібрану випадкову величину, точний розподіл якої відомий і здебільшого зведено в таблиці. Ця величина називається критичною Ккр , якщо вона віддаляє критичну ділянку від ділянки прийняття гіпотези.

Відмінності можна вважати випадковими, якщо емпіричний критерій не досягає потрібного порога ймовірності.
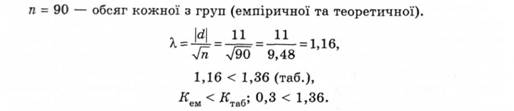
Відмінності недостовірні, оскільки немає достатніх підстав вважати, що вибірки взяті з двох генеральних сукупностей, які відрізняються своїми розподілами:
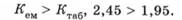
Відмінності не можуть вважатися випадковими, вони достовірні. Вибірки взяті з двох генеральних сукупностей, які явно розрізняють за своїми розподілами.
Статистична оцінка достовірності різниці між середнім показником двох груп експериментальних даних.
Завдання цього типу дуже часто трапляються в практиці психологів різних профілів. Питання про те, чи відрізняються між собою дві групи спостережень виникає буквально всюди.
Розглянемо t -критерій Стьюдента. Цей критерій використовують для оцінки статистичної значимості різних вибіркових середніх двох розподілів первинних величин. Статистична значимість різниці середніх арифметичних величин вираховується за формулою:

Приклад. У табл. 5.18 наведено середньогрупові величини шістнадцяти змінних методики Кеттела. Ці дані отримано усередненням трьох статистично однорідних вибірок, які відрізняються лише мірою вираженості психічної напруги. У кожній вибірці було представлено по 28 осіб від 26 до 80 років. Завдання аналізу — виявити індивідуально-особистісні властивості регулювальників кольорових телевізорів, які суттєво впливають на виникнення психічної напруги. Відправним пунктом аналізу були середньогрупові величини, отримані методом профілювання.
Таблиця 5.18. Статистичні параметри показників для груп, які розрізняють за рівнем психічної напруженості
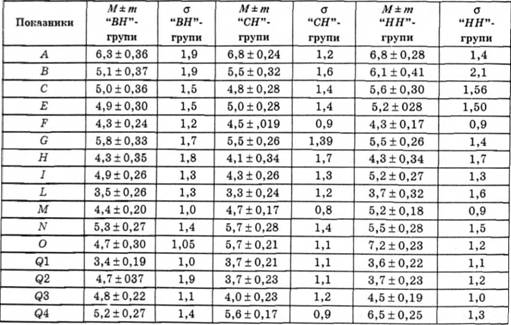
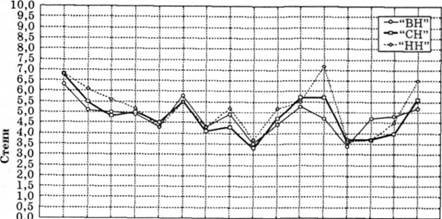
З табл. 5.14 видно, що значимі відмінності при порівнянні високо- і низьконапружених ("ВН" і "НН") регулювальників виявлено у п'яти особистісних властивостях (групу середньо-напружених надалі позначатимемо як "СЯ"). Різниця середніх статистично значима на рівні р ≤ 0,001, 0,01, 0,05.
Аналіз експериментального матеріалу показав, що найбільш суттєві відмінності виявлено перш за все за показником самоконтролю (Q2) й емоційної нестійкості (С). Гірші показники — за рівнем інтелекту (В), суб'єктивності, замкненості (М), тривоги, схильності до самозвинувачення (О), фрустрованості, напруженості інстинктивної сфери (Q4).
Особистісний профіль за методикою 16PF Кеттела подано на рис. 5.3.
Таблиця 6.14. Значення величин t-критерію Стьюдента* при порівнянні показників груп, які розрізняють за рівнем психічної напруги
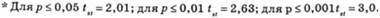
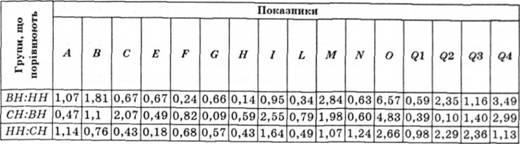

Однак психодіагносту треба пам'ятати, що існування статистично значимої різниці середніх значень є важливим, але не єдиним аргументом на користь наявності або відсутності зв'язку (залежності) між явищами або змінними. Тому потрібно використовувати й інші аргументи кількісного та змістовного обґрунтування можливого зв'язку.
Статистично значимий достовірний зв'язок — необхідна й недостатня умова існування змістовної взаємозалежності змінних.
Статистичне дослідження міри взаємозв'язку між двома явищами. Міра зв'язку між експериментальними даними (rху).
У будь-якому трудовому процесі фактори, які його становлять, перебувають у тісному взаємозв'язку. Вміння змінити один фактор так, щоб отримати відповідну зміну іншого, зробить трудовий процес оптимальнішим.
Будь-яка галузь сучасної науки прагне здебільшого виразити відкриті нею закони у формі математичної моделі, тобто у виді тих чи інших співвідношень між показниками, які характеризують різні сторони пізнаних явищ. Таку модель відповідних співвідношень між показниками називають функціональною залежністю. Функціональний зв'язок відображає чітку однозначну залежність, при якій зміна одного певного фактора обов'язково призводить до однозначної зміни іншого. Знання функціональної залежності дає змогу передбачити знання залежної величини (функції) при будь-якому значенні "керуючої" нею величини (аргументу).
Навіть у точних науках, які володіють більшими можливостями, стандартизувати всі фактори, крім тих, які вивчають, не завжди вдається зблизити умови проведення суміжних дослідів. Ще важче досягти того в психологічних (педагогічних) дослідженнях. Причин дуже багато: по-перше, багато факторів, які впливають на хід навчання і виховання, невідомо (наприклад, певні події в житті досліджуваного, неможливо детально врахувати його життєвий досвід, неможливо повністю ізолювати людину в експерименті від впливу середовища, яке постійно змінюється та ін.); по-друге, практично неможливо підібрати зовсім однакових людей для порівняльного експерименту; по-третє, неможливо знайти двох однакових педагогів для проведення занять в експериментальних і контрольних групах; по-четверте, суб'єктивні переживання досліджуваних, їх ставлення до занять, експерименту недоступні для безпосереднього вивчення. Людина як об'єкт дослідження дуже складна у своїх виявленнях, щоб її поведінку можна було вкласти в якусь формулу. Саме тому як в біології, так і в психології й педагогіці, здебільшого уникають говорити про функціональні зв'язки й основну увагу приділяють дослідженню статистичних зв'язків або кореляції.
Кореляція дає змогу знаходити статистично достовірні кількісні міри зв'язку (табл. 5.15) в тих випадках, коли певному фактору відповідає не одне, а кілька значень якого-небудь іншого фактора, причому варіюючих у певних межах. Зв'язок у цьому випадку виражатиметься середніми значеннями, які отримали багатьма змінами (замірів).

Корелюючи фактори поділяють на причинні, які видозмінюються і першими, спричиняють зміну інших факторів; наслідкові, які видозмінюються під впливом причинних факторів. Наслідкові фактори можуть набувати багато значень у відповідних межах.
Дослідників часто цікавить, як пов'язані між собою дві змінні в певній групі осіб (класі, школі, нації тощо). Наприклад, чи мають учні, які навчилися читати раніше за інших, тенденцію до кращої успішності в шостому класі? Чи простежуються у великих класах менші успіхи в набуванні знань за семестр, ніж у менших класах? Чи пов'язана тривалість роботи педагога в школі безпосередньо зі середньою зарплатою? Щоб відповісти на такі запитання, ми повинні простежити за кожною змінною для груп об'єктів (типових представників, якими можуть бути класи, школи, райони тощо).
Дані, зібрані для відповіді на одне з подібних запитань, можуть виглядати так, як наведено в табл. 5.16. У цьому прикладі змінними, які вивчали у 12 учнів, були оцінки IQ, що визначали за допомогою тесту інтелекту Векслера в шостому класі, і успішність у середній школі з хімії, яку оцінювали на підставі тесту, складеного з 35 запитань.
Таблиця 5.16. Дані оцінок рівня інтелекту й оцінок тесту успішності з хімії
| Порядковий номер | IQ(х) | Оцінка тесту успішності з хімії |
| 1 | 120 | 31 |
| 2 | 112 | 26 |
| 3 | 110 | 19 |
| 4 | 120 | 24 |
| 5 | 103 | 17 |
| 6 | 126 | 28 |
| 7 | 113 | 18 |
| 8 | 114 | 20 |
| 9 | 106 | 16 |
| 10 | 108 | 15 |
| 11 | 128 | 27 |
| 12 | 109 | 19 |
Зв'язок між двома змінними можна зобразити графічною діаграмою розсіювання. Діаграма розсіювання для цього прикладу зображена на рис. 5.4. На діаграмі розсіювання показники кожного учня позначені крапкою. Мітка розміщена у місці перетину прямих ліній, які проведені через відмітку показника IQ перпендикулярно до осі X і через відмітку показника тесту з хімії перпендикулярно до осі У для кожного учня. З діаграми на рис. 5.4 видно, що є слабкий позитивний зв'язок між цими показниками. Узагальненою мірою цього зв'язку є коефіцієнт кооеляпії Пірсона.

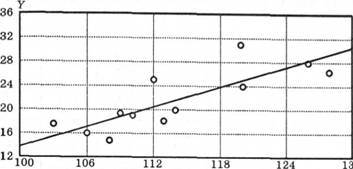
X
Рис. 5.4. Діаграма розсіювання, яка відображає зв'язок IQ(х) з успішністю з хімії (Y) для 12 школярів
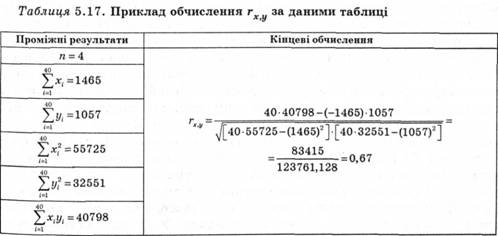
Приклад обчислення rх.y. (табл. 5.17) Щоб проілюструвати обчислення rх.y. за формулою, треба використати деякі дані тесту на виявлення загальних і спеціальних здібностей. Дослідник вивчає зв'язок двох типів розумових здібностей учнів неповної середньої школи: абстрактне і вербальне мислення. Розроблено два тести: для замірів нахилів до абстрактного мислення (X) і до вербального мислення (У). Обидва тести запропонували 40 школярам молодшого класу неповної середньої школи в одному місті з 30 тис. жителів. Результати досліджень 40 учнів наведено в табл. 5.18. Кожен тест мав 50 запитань, а результат — кількість правильних відповідей.
Таблиця 5.18. Вихідні оцінки здатності до абстрактного та вербального мислення 40 школярів неповної середньої школи
| Порядковий номер | X,абстрактне мислення | У, вербальне мислення | Порядковий номер | X, абстрактне мислення | У, вербальне мислення | Порядковий номер | X, абстрактне мислення | У вербальне мислення |
| 1 | 19 | 17 | 16 | 82 | 24 | 81 | 31 | 16 |
| 2 | 32 | 7 | 17 | 48 | 45 | 32 | 41 | 87 |
| 3 | 88 | 17 | 18 | 48 | 26 | 33 | 42 | 37 |
| 4 | 44 | 28 | 19 | 38 | 16 | 34 | 24 | 14 |
| 5 | 28 | 27 | 20 | 47 | 26 | 35 | 43 | 41 |
| 6 | 85 | 81 | 21 | 38 | ЗО | 36 | 36 | 19 |
| 7 | 39 | 20 | 22 | 25 | 18 | 37 | 39 | 18 |
| 8 | 39 | 17 | 23 | 35 | 26 | 38 | 39 | 39 |
| 9 | 44 | 35 | 24 | 22 | 17 | 39 | 39 | 37 |
| 10 | 44 | 48 | 25 | 40 | 17 | 40 | 48 | 47 |
| 11 | 24 | 10 | 26 | 42 | 26 | |||
| 12 | 87 | 28 | 27 | 41 | 16 | |||
| 18 | 29 | 13 | 28 | 41 | 87 | |||
| 14 | 40 | 48 | 29 | 87 | 26 | |||
| 15 | 42 | 45 | 30 | 30 | 21 |
Процедура експерименту.
Визначення цільових ознак.
Визначення прогностичних ознак.
Виявлення функції зв'язку.
Інтерпретація й аналіз даних.
Форма подання результатів дослідження, завершення.
Універсальні психодіагностичні методики.
Оцінка психічного розвитку.
Розділ 6. ПСИХОЛОГІЧНЕ ВИВЧЕННЯ ПРОФЕСІЙ