Математична статистика - Руденко В.М. - Атрибутивні розподіли

Атрибутивні розподіли використовуються у разі номінальних (категоріальних) типів вимірювань властивостей досліджуваних об'єктів.

Приклад 2.5. Розрахувати розподіли осіб за результатами тестування властивостей вищої нервової діяльності (ВНД) 16 осіб (рис. 2.18). Побудувати відповідні графіки розподілу.

Послідовність рішення:

o вибіркові емпіричні дані внести у стовпчики А:Б;

o згідно з типом ВНД кожній особі надати відповідний атрибут х_і, наприклад, "холерик" - 1; "сангвінік" - 2 і т.д. (стовпчики С:Б і Е:Б);

o для розрахунку абсолютних частот м_і у комірку в3 внести вираз =СЧЕТЕСЛИ($0$3:$0$18;Р3). Аналогічні вирази внести в комірки 04:в6;

o для розрахунку загальної кількості об'єктів п у комірку в7 внести вираз =СУММ(03:в6);

o для розрахунку відносних частот п/п у комірку Н3 внести вираз: =в3/$в$7, аналогічні вирази внести у комірки Н4:Н6. У комірку Н7 внести вираз =СУММ(Н3:Н6).

Рис. 2.18. Розрахунки розподілу осіб за типами ВНД

Як бачимо з розподілу осіб за типами ВНД (рис. 2.18), у вибірці маємо 3 особи за типом "холерик" (18,75%), 7 - за типом "сангвінік" (43,75%), 5 -"меланхолік" (31,25%) і 1 - "флегматик" (6,25%).

Для ілюстрації атрибутивних розподілів використовують два найбільш розповсюджені типи графіків: гістограму (рис. 2.19) і кругову діаграму (рис. 2.20).

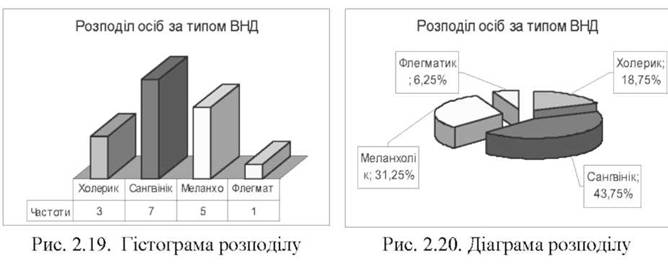
Атрибутивні розподіли дають можливість оцінити властивості в абсолютних і відносних значеннях, наприклад, співвідношення різних типів ВНД, переважний тип ВНД - на графіках це "сангвінік", який складає 43,7% осіб вибірки (рис. 2.19 і 2.20).

Ранжировані розподіли

Ранжировані розподіли використовують у разі порядкових (рангових) типів вимірювань, наприклад, визначення рейтингу успішності якоїсь діяльності. Ранжування припускає домовленість про відповідність певного рангу певному значенню емпіричних даних.

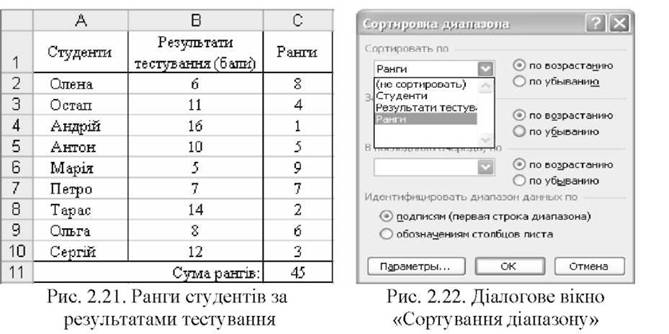
Приклад 2.6. Виконати ранжування студентів за результатами тестування (див. стовпчики А:В таблиці рис. 2.21).

Послідовність рішення:

o у комірку С2 внести математичний вираз, який визначить ранг значення комірки В2 серед даних вибірки в діапазоні В$2:В$10:

=СЧЕТ(В$2:В$10) + 1-((СЧЕТ(В$2:В$10) + 1- РАНГ(В2;Б$2:Б$10;

1) - РАНГ(В2;В$2:В$10; 0))/2+РАНГ(В2;В$2:В$10;1));

o скопіювати аналогічні вирази у комірки С3:С10;

o у комірку С11 внести вираз =СУММ(С2:С10), який дасть суму рангів;

o упорядкувати дані діапазону А2:С10 за рангом за допомогою команд головного меню MS Excel [Дані -> Сортування] і діалогового вікна (рис. 2.22);

o отримати упорядковані стовпчики таблиці за рангом (рис. 2.23);

o відобразити рейтинговий список студентів графічно (рис. 2.24).

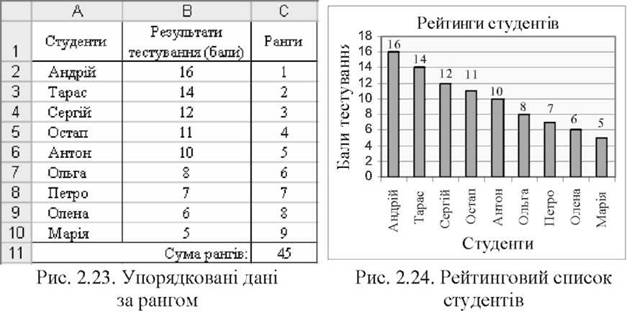
Ранжировані розподіли дають можливість наочної візуалізації результатів

досліджень певної властивості серед об'єктів дослідження у напрямах їх збільшення або зменшення.

Основними способами представлення емпіричних розподілів є табличний, графічний та аналітичний.

Табличний спосіб представлення розподілів продемонстровано, наприклад, на рис. 2.16. По-різному називають такі таблиці: таблицею емпіричних частот або табличною формою представлення розподілу. Табличний спосіб є основним розрахунковим методом і передумовою його графічної форми. Разом вони дають цілісне уявлення щодо властивостей вибірки.

Графічний спосіб представлення - це відображення розподілу графічними засобами, серед яких найпоширенішими є гістограма, полігон і лінійний графік. На рис. 2.25 - 2.27 показано диференціальний відносний розподіл незгрупованих частот у трьох варіантах. Комбіновані способи представлення, які об'єднують у межах однієї графічної форми різні типи розподілу (диференціальний та інтегральний), можна побачити на рис. 2.17.

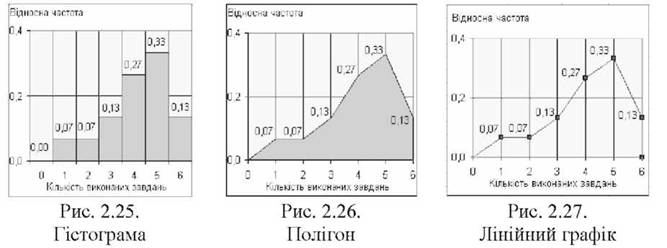
Аналітичний спосіб представлення передбачає використання математичної емпіричної функції розподілу, наприклад, щільності Дх_;), або розподілу Р(х,). Так, щільність розподілу з рис. 2.25 - можна представити за допомогою емпіричної функції:

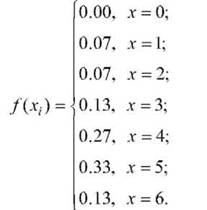
Аналогічно можна представляти й розподіли інтегральних частот. Статистичні розподіли є первинною базою, навколо якої об'єднуються основні методи математичної статистики.

Запитання. Завдання.

1. Охарактеризуйте основні групи статистичних показників вибірки.

2. Що таке варіаційний ряд і статистичний розподіл?

3. Чим відрізняються між собою варіаційні, атрибутивні та ранжирувані розподіли?

4. Яка різниця між абсолютними і відносними розподілами частот?

5. Як розраховуються незгруповані і згруповані розподіли частот?

6. Чим відрізняються диференціальні та інтегральні розподіли частот?

7. Які типи графіків розподілу частот вважаються найпоширенішими?

8. Повторіть математичні процедури завдань за прикладами 2.1 - 2.6.

9. Виконайте лабораторні роботи № 1 і № 2.