Статистика - Опря А.Т. - ТЕМА 5. АНАЛІЗ РЯДІВ РОЗПОДІЛУ

§ 5.1. Поняття про статистичні ряди розподілу

Маючи в розпорядженні дані статистичного спостереження, що характеризують те чи інше явище, перш за все необхідно їх впорядкувати, тобто надати характер системності.

Англійський статистик У.Дж.Рейхман з приводу неупорядкованих сукупностей образно сказав, що зіткнутися з масою неузагальнених даних рівнозначно ситуації, коли людину кидають у лісових хащах без компаса. Що ж собою являє систематизація статистичних даних у вигляді рядів розподілу?

Статистичний ряд розподілу - це впорядковані статистичні сукупності (табл. 17). Найпростішим видом статистичного ряду розподілу є ранжированний ряд, тобто ряд чисел, що знаходиться в порядку зростання чи спадання варіюючої ознаки. Такий ряд не дозволяє судити про закономірності, закладені в розподілених даних: біля якої величини групується більшість показників; які є відхилення від цієї величини; яка загальна картина розподілу. З цією метою групують дані, показуючи, як часто зустрічаються окремі спостереження в загальному їх числі (Схема 1).

Таблиця 17

Загальний вигляд статистичних рядів розподілу

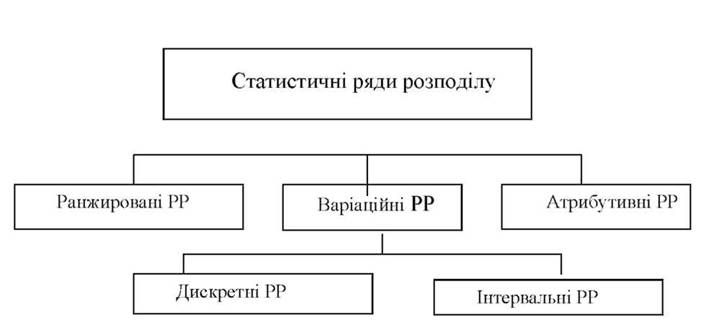
Схема 1. Схемастатистичних рядів розподілу

Розподіл одиниць сукупності за ознаками, що не мають кількісного виразу, називається атрибутивним рядом (наприклад, розподіл підприємств за їх виробничим напрямом).

Ряди розподілу одиниць сукупності за ознаками, що мають кількісний вираз, називаються варіаційними рядами. У таких рядах значення ознаки (варіанти) знаходяться в порядку зростання чи спадання.

У варіаційному ряді розподілу розрізняють два елементи: варіанта і частота. Варіанта - це окреме значення групувальної ознаки, частота - число, яке показує, скільки разів зустрічається кожна варіанта.

У математичній статистиці обчислюється ще один елемент варіаційного ряду - частість. Остання визначається, як відношення частоти випадків даного інтервалу до загальної суми частот. Частість визначається в частках одиниці, відсотках (%) в проміле (%о).

Таким чином, варіаційний ряд розподілу - це такий ряд, у якому варіанти розташовані в порядку зростання або спадання, вказані їх частоти або частості. Варіаційні ряди бувають дискретні (переривні) і інтервальні (непереривні).

Дискретні варіаційні ряди - це такі ряди розподілу, в яких варіанта як величина кількісної ознаки може приймати тільки певне значення. Варіанти різняться між собою на одну чи кілька одиниць.

Так, кількість вироблених деталей за зміну конкретним робітником може виражатися тільки одним певним числом (6, 10, 12 і т.д.). Прикладом дискретного варіаційного ряду може бути розподіл працівників за кількістю вироблених деталей (табл. 18).

Таблиця 18

Дискретний ряд розподілу_

Інтервальні (непереривні) варіаційні ряди - такі ряди розподілу, в яких значення варіанти дано у вигляді інтервалів, тобто значення ознак можуть відрізнятися одне від одного на скільки завгодно малу величину. При побудові варіаційного ряду непереривної ознаки неможливо вказати кожне значення варіанти, тому сукупність розподіляється за інтервалами. Останні можуть бути рівні і нерівні. Для кожного з них вказуються частоти або частості (табл. 19).

В інтервальних рядах розподілу з нерівними інтервалами обчислюють такі математичні характеристики, як щільність розподілу і відносна щільність розподілу на даному інтервалі. Перша характеристика визначається відношенням частоти до величини того ж інтервалу, друга - відношенням частості до величини того ж інтервалу. Для наведеного вище прикладу щільність розподілу на першому інтервалі становитиме 3:5 = 0,6, а відносна щільність на цьому інтервалі - 7,5:5= 1,5%.

Таблиця 19

Інтервальний ряд розподілу _