Знаючи математичні властивості дисперсії, можна спростити вирахування її величини. Розглянемо їх.
1. Якщо із усіх значень варіант відняти постійне число А, то величина дисперсії не зміниться
СТ( *,-А) = ^ .
Таким чином, середній квадрат відхилень можна обчислити не за величинами варіант, а за відхиленням їх від якогось постійного
ґг2 = ґг2
числа, тобто ('o-Ау
2. Якщо значення варіант поділити на постійне число А, то величина дисперсії зменшиться в А2, а середнє квадратичне відхилення в А разів:
<у =ст2: А1.
(7)
Із цього випливає, що всі варіанти можна поділити на будь-яке постійне число, обчислити середнє квадратичне відхилення, а потім
а2 =ог А2
помножити його на це постійне число: ^А >
3. Якщо вирахувати середній квадрат відхилень від будь-якої величини (А), що відрізняється в тій чи інший мірі від середньої (х), то величина його завжди буде більше середнього квадрата відхилень, обчисленого відносно середньої (ол 2).
Отримане перевищення дорівнює квадрату різниці між середньою і умовно узятою величиною, тобто 1 х -А /2. Це все можна подати у такому запису:
а2А = а2 + (~х - А)2 або а2А = а2 - (х - А)
Розглянута властивість середнього квадрата відхилень дозволяє зробити висновок про те, що дисперсія від середньої (ст2 ) завжди
2
менша за дисперсії, обчислені від будь-яких інших величин ад , тобто вона має властивість мінімальності.
4. Дисперсія постійної величини дорівнює нулю ("^'^ ~0). Ця властивість випливає з того, що дисперсія є показником розсіювання варіант навколо середньої арифметичної, а середня арифметична постійної величини дорівнює цій величині.
Ряд властивостей дисперсії ґрунтується на рівності ° = х ~(х) , Тобто дисперсія дорівнює різниці між середньою арифметичною квадратів варіант і квадратом середньої арифметичної.
5.3.2. Загальна, міжгрупова і внутрішньогрупова дисперсія
Якщо всі значення ознаки статистичної сукупності (генеральної або вибіркової) розділити на декілька груп і розглядати кожну з них як самостійну (окрему) сукупність, то виникає необхідність обчислення трьох видів дисперсій: загальної, міжгрупової і внутрішньогрупової.
Загальна дисперсія - це середній квадрат відхилень значень ознак всієї сукупності відносно загальної середньої.
Міжгрупова дисперсія - це середній квадрат відхилень групових середніх відносно загальної середньої.
Внутрішньогрупова дисперсія - це середня арифметична часткових (групових) дисперсій, зважена обсягами груп.
У таблиці 27 наведена структурні формули обчислення названих видів дисперсій.
Таблиця 27
Формули для обчислення дисперсій

Приклад. За даними врожайності зернових культур 57 підприємств визначити загальну, міжгрупову і внутрішньогрупову дисперсії, утворивши сім груп підприємств за рівнем урожайності.
Для обчислення загальної дисперсії необхідно побудувати дискретний ряд розподілу (табл. 28).
За розрахунковими даними цього статистичного ряду визначаємо
середню арифметичну ( х)і величину загальної дисперсії ( за'-):
- Іхпг 1535.5 " 2 І(хг -х)2пі 1399.06 "",
х = -- =-= 26.9; ашг =---- =-= 24.5.
І,пі 57 І,пі 57
Таблиця 28
Вихідні і розрахункові дані для обчислення загальної дисперсії __ (дискретний ряд)_
Варіанта , хі | Частота пі | Розрахункові дані | |||
хі п | хі - Х | ( ХІ - Х )2 | ( Хі - х)2 щ | ||
17,5 | 1 | 17,5 | -9,4 | 88,36 | 88,36 |
17,6 | 2 | 35,2 | -9,3 | 86,49 | 172,98 |
36,2 | 3 | 108,6 | 9,3 | 86,49 | 259,47 |
37,6 | 2 | 75,2 | 10,7 | 114,49 | 228,98 |
Разом | 57 | 1535,3 | X | X | 1399,06 |
Для визначення міжгрупової дисперсії необхідно обчислити групові
середні (хі) і знайти загальний об'єм їх варіювання відносно загальної середньої (І(хі - х)2 N). За розрахунковими даними таблиці 29 визначаємо розмір міжгрупової дисперсії:
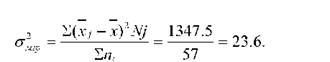
Таблиця 29
Вихідні і розрахункові дані для обчислення міжгрупової дисперсії
Інтервал (група) | Середня по групі, | Обсяг груп, | Розрахункові дані | ||
х] - X | (х, - х)2 | (х, - х)2 | |||
17,5-20,5 | 18,9 | 9 | -8,0 | 64,00 | 576,0 |
20,5-23,5 | 21,9 | 6 | -6,0 | 25,0 | 150,0 |
23,5-26,5 | 25,4 | 9 | -1,5 | 2,25 | 20,3 |
26,5-29,5 | 28,2 | 13 | 1,3 | 1,69 | 22,0 |
29,5-32,5 | 30,8 | 15 | 3,9 | 15,21 | 228,0 |
32,5-35,5 | 34,0 | 3 | 7,1 | 50,41 | 151,2 |
35,5-38,5 | 36,9 | 2 | 10,0 | 100,00 | 200,0 |
Разом | X | 57 | X | X | 1347,5 |
Щоб визначити внутрішньогрупову дисперсію, необхідно розрахувати часткові дисперсії у розрізі семи груп. Маючи групові середні |Х] |, знаходимо
..... . у і., ..
по кожної групі відповідну часткову дисперсію і ' 1. За даними прикладу, який
(гг2 (Т2 (Т2 (Т2 )
розглядається, необхідно обчислити сім таких дисперсій( 1, 11, 111 гп). Необхідні проміжні дані для їх обчислення наведено в таблиці 30.
Таблиця 30
Вихідні і розрахункові дані для обчислення внутрішньогрупової дисперсії (розрахунок часткових дисперсій) ( ')
Інтервал (група) | Варіанта, хі | Частота, п, | Розрахункові дані | ||||
~х.і | ( Х1 - X] )2 Па | ||||||
17,5-20,5 | 17,5 | 1 | 17,5 | -1.4 | 1,96 | 1,96 | |
( хі = 18,9) | 17,6 | 2 | 35,2 | -1.3 | 1,69 | 3,38 | Б(х; - хі )2 п Nі |
Всього | X | 9 | 170,0 | X | X | 9,05 | 9.051.0 = 9 |
... | ... | ... | ... | ... | ... | ... | ... |
35.5-38,5 | 36,2 | I | 36,2 | -0.7 | 0,49 | 0,49 | |
(- 36.9) | 37,6 | I | 37,6 | 0.7 | 0.49 | 0,40 | І(х, - хРШ )2 пі |
Всього | X | 2 | 73,8 | X | X | 0,98 = | = 098 = 0,49 2 |
Початку обчислень часткових дисперсій передує розрахунок групових
- _ їх- _ 170
середніх (Хі). Так, для першого інтервалу 9 =18,9. Аналогічно
розраховуємо середні для інших груп. Потім знаходимо окремі дисперсії °і , величини яких становлять: аі = 1,0; ^ = 0,43; агл = 1,12; Сіу = 0.68; °у = 1.09; <угі - 0,58; суп - 0,49 (послідовність розрахунку показано тільки для першого і сьомого інтервалів).
Маючи обчислені значення часткових дисперсій, знаходимо величину внутрішньогрупової дисперсії:
ст2 = о) Х1 + о]1Па + Ощіїщ +... + о2ш^т = ** N + N1 + Жш І.... + N,1,,
_ 1х 9 + 0.43 х 6 +1.12 х 9 + 0.68 х13 +1.09 х15 + 0.58 х 3 + 0.49 х 2 _ 49.57 _ 0 87 ^ 0 9 9 + 6 + 9 +13 +15 + 3 + 2 ' 57 ~ . ~ .
Відповідно до правила складання дисперсій, яке випливає з доказу, що якщо сукупність складається з кількох груп, то загальна дисперсія дорівнює сумі внутрішньогрупової і міжгрупової дисперсій, маємо:
ст2 =ст2 +ст2 = 23,6 + 0,9 = 24,5
общ "ігр вгр ' ' '
За раніше наведеними розрахунками, величина загальної дисперсії за! дорівнює 24,5, що підтверджує вірність виконаних обчислень.
Теоретичний і практичний інтерес правила додавання дисперсій полягає у тому, що, знаючи дві величини дисперсії, на основі наведеної рівності завжди можна знайти третю. Наприклад:
222 сг = о -о
вгр гаг жгр
Маючи величини міжгрупової і загальної дисперсій, можна мати уяву про силу впливу групувальної ознаки. Про це мова піде при вивченні питань кореляційного і дисперсійного методів аналізу.
5.3.3. Дисперсія альтернативних ознак
Перш ніж розглянути питання про дисперсію альтернативних ознак, слід нагадати, що під альтернативною ознакою розуміють таку ознаку, якою одні варіанти наділені, а другі - ні. Так, якщо у вибірці, яка складається з п одиниць і п" одиниць, наділених даною ознакою, то їх частка ¥ у вибірковій сукупності становитиме:
п"
№ = -.
п
Розрахунок загальної, міжгрупової і внутрішньогрупової дисперсій для альтернативних ознак поданий за формулами в таблиці 31.
Таблиця 31
_Формули обчислення дисперсій для альтернативних ознак_
Вид дисперсії | Формула | Примітка |
Загальна | а1, = и(1- И) | і - частка одиниць наділених даною ознакою |
Міжгрупова | сг2 -- | і,- - частка одиниць, наділених даною ознакою в і -й групі |
п - число одиниць в і - й групі | ||
Внутрішньогрупова | 2 Т.и>і (1 - иі1 )п Ъп1 | ^п - об'єм вибірки и, = и) |
Розглянемо послідовність розрахунку названих видів дисперсій на конкретному прикладі. У таблиці 32 представлена вибірка 60 підприємств, розподілених за виробничим типом на дві групи з обсягом п кожної і виділенням альтернативної ознаки - кількості збиткових підприємств ().
Підставляючи розрахункові дані таблиці 32 у формули відповідних видів дисперсій, одержимо:
аі = №(1 - і) = 0,233/1 - 0,233 / = 0,179; а2 =І(і, -1)2 п, = 0,134 = 0,002;
мі 60
2 (1 ~ 1,)п, 10,6
=--- -:- = 0,177.
^■Щ = 60
Таблиця 32
Вихідні і розрахункові дані для обчислення дисперсій
Число Розрахункові дані | ||||||||
Група | Обсяг груп, п | одиниць у групі, наділених даною ознакою, п" | п" И[ =- п | И = (1 - И>1 ) | И(1 - и)п | И - и | (И - И)2 | И - и)2 п |
I | 40 | 8 | 0,200 | 0,16 | 6,4 | -0,03 | 0,0009 | 0,036 |
П | 20 | 6 | 0,300 | 0,21 | 4,2 | 0,07 | 0,0049 | 0,098 |
Всього | 60 | 14 | 0,233 (14:60) | X | 10,6 | X | X | 0,134 |
Ґрунтуючись на правилі додавання дисперсій, маємо:
^ = +°1 або 0,179 =0,002+0,177; 0,179= 0,179.
Середнє квадратичне відхилення альтернативної ознаки в
даному випадку легко знайти шляхом добування кореня з ст" ,
тобто : ° = >/-№) = >/0^179 = 0.42.
§ 5.4. Моменти статистичного розподілу
§ 5.5. Характеристика асиметрії і ексцесу
ТЕМА 6. АНАЛІЗ ПОДІБНОСТІ РОЗПОДІЛІВ
§ 6.1. Статистична оцінка параметрів розподілу
§ 6.2. Закони розподілу вибіркових характеристик
6.2.1. Загальне поняття законів розподілу
6.2.2. Нормальний розподіл
6.2.3. Розподіл Стьюдента
6.2.4. Розподіл Хі- квадрат