Варіаційний ряд розподілу може характеризуватися системою статистик, які мають загальний математичний вираз і носять назву моментів розподілу. В цій системі знаходять своє відображення (місце) такі узагальнюючі характеристики ряду, як середня і дисперсія.
Система моментів розподілу вперше була розроблена російськім математиком П.Л.Чебишевим.
Загальний математичний вираз моменту розподілу (загального емпіричного моменту) має вигляд:
м =І(*-- А)" п
" 1щ
де м" - момент к-го порядку; *< - варіанти ряду; - частоти ряду;
к, А - постійні числа [к-порядок (степінь), А - довільне постійне число (несправжній нуль)].
Слід пам'ятати, що при розрахунку моментів статистичних розподілів осредняєтся к- та степінь відхилень значень ознаки (варіанти) Хі від деякої постійної величини (А).
Залежно від того, яка величина прийнята за умовний початок (А), загальна система моментів може бути подана підсистемами початкових, центральних і нормованих моментів.
Якщо умовний початок А = о, отримують підсистему початкових моментів. Початковий момент к-го порядку (к-ї степені)
виражається формулою:
1.x' п, М =--
де м" - початковий момент к-го порядку;
Іх п - сума добутків варіант к -ї степеня на їх частоти;
' - сума частот.
При к= 0 момент називається початковим моментом нульового порядку, при к= 1 - початковим моментом 1-го порядку при к= 2 -початковим моментом 2-го порядку і т.д.
Розрахунок величин початкових моментів від нульового до четвертого порядків представлений схематично в таблиці 33.
При А=х одержуємо підсистему центральних моментів. Центральний момент к -го порядку виражається формулою:
Як видно з наведеної формули, центральні моменти являють собою середні із різних степенів відхилень від середньої арифметичної.
Таблиця 33
Розрахунок підсистеми початкових моментів_
Порядок (степінь) к, | Формула | Зміст |
0 | 0 Ъп, | 1 |
1 | ,, Ех'п М,-- | х (середня арифметична) |
2 | М2 =-- | %1 (середня квадратів варіант) |
3 | 3 щ | х3 (середня кубів варіант) |
4 | х4 (середня четвертих степенів варіант) |
Схема розрахунку підсистеми центральних моментів від нульового до четвертого порядків наведена в таблиці 34.
Обчислення центральних моментів можуть бути значно спрощені, якщо знати властивості цієї підсистеми моментів. Розглянемо їх.
1. Якщо усі варіанти статистичного ряду зменшити або збільшити на якесь постійне число С, то величина центрального моменту к -го порядка не зміниться. Так, якщо центральний момент розрахувати за зменшеними (~с) або збільшеними (+ с) варіантами, то = .
Таблиця 34
Розрахунок підсистеми центральних моментів_
Порядок (степінь),к | Формула | Зміст | Взаємозв'язок з початковими моментами |
0 | Б(х; - х)° щ Мі - " Іп, | 1 | - |
1 | Б( х1 - х)1пі | 0 | М, -М, |
2 | Б(х; - х)2 п і | а2 | м2 - м,2 |
3 | Б( х1 - х)3 п | Використовується для характеристики асиметрії розподілу | м 3 - зм 2м1 + 2м3 |
4 | Б(х; - х)4 п і Ъп1 | Використовується для характеристики гостровершиності | М4 - 4М3М1 + 6М2М2 - 3М4 |
2. Якщо усі варіанти статистичного ряду зменшити або збільшити в одне і те ж число раз (г), то центральний момент к -го порядку зменшиться або збільшиться у їк разів. Тобто якщо
центральний момент к -го порядку ( ) розраховувати за збільшеними у г разів варіантами (Х 2), то величина його
становитиме = ^2 . Аналогічно одержуємо за зменшеними в г разів
- м
варіантами: ^ .
Отже, одержавши центральний момент ) За зміненим рядом [напр., *< = (х' ~с): 2 ], можна обчислити центральний момент к -го порядку для початкового ряду. Для випадку, коли варіанта зменшена на С одиниць, і це значення (*< ~с) у свою чергу зменшити у % разів [(*, -с): г 1, т0 центральний момент (к -го порядку буде дорівнювати:
[і = [і1 -їК.
Знання розглянутих вище властивостей підсистеми центральних моментів дозволить значно скоротити обсяги обчислювальних робіт, особливо у тих випадках, коли вибіркова сукупність представлена громіздкими розмірами величин досліджуваних ознак.
Як було зазначено раніше, центральний момент другого порядку (^2) являє собою дисперсію (ст2). Якщо корінь квадратний з дисперсії (тобто середнє квадратичне відхилення) прийняти за стандарт ^Л^"2), то відношення центрального моменту к-го порядку до стандарту в к-тій степеня буде називатися нормованим моментом. Загальна його формула має вигляд:
т = Мі =
ЧМ2)1 ° .
Згідно з наведеною вище формулою нормовані моменти від першого до четвертого порядків можна записати у такому
ВИГЛЯДі: о о а а о о .
Послідовність розрахунку моментів розподілу полягає у складанні на першому етапі робочих таблиць. В останні заносяться вихідні і розрахункові дані з тим, щоб у подальшому їх використати для розрахунку тієї чи іншої формули моменту розподілу.
Наведемо форми таких таблиць у вигляді макетів (табл. 35, 36).
Таблиця 35
Вихідні і розрахункові дані для обчислення початкових __моментів ряду розподілу_
Варіанта, Хі | Частота | Розрахункові дані | ||||||
2 Хі | 3 Хі | х4 | х1п1 | х2пі | х]пі | 4 | ||
Всього | X | X | X | |||||
Таблиця 36
Вихідні і розрахункові дані для обчислення центральних __моментів ряду розподілу_
Варіанта,Хі | Частота, | Розрахункові дані | |||||||
(х, - х) | (*, - х)3 | (*, - х)4 | (х1 - х)пі | (хі - х)2пі | (хі - *)3 пі | (хі - х)4пі | |||
Всього | X | X | X | X | X | ||||
Розглянуті ваше підсистеми моментів використовуються як статистичні характеристики розподілу. У статистичних розрахунках іноді звертаються до так званих умовних моментів. Одержують цю форму моментів при А = Х0 , де х" - деяка варіанта (умовний початок). За Л0 приймається величина досліджуваної ознаки, яка близька до
середньої варіанти (х) , тобто до варіанти, розміщеної приблизно в середині варіаційного ряду. Така варіанта , як правило, має найбільшу частоту.
Умовний момент к-го порядку має вигляд:
ЦХ, - Х0) кпі ш, =-
1 І-
Як видно з формули, умовні моменти являють собою середні різних степенів із відхилень варіант від умовного початку (несправжнього нуля). Умовні моменти першого, другого, третього і вищого порядків будуть виражатися відповідними формулами:
Е(хі -Х0)1 п, Е(хі - Х0)2п, Е(Х. - Х0)3п ш1 =- ш2 =- ш3 =-
? ? 11 -А-
Відзначимо, що умовні моменти першого і другого порядків використовуються для спрощення розрахунків відповідно середньої арифметичній і дисперсії.
Для інтервального варіаційного ряду з рівними інтервалами розрахунок умовних моментів може бути значно спрощений, якщо відхилення (~ ^о) розділити на величину інтервала (і). Знаючи, що в основі дискретного ряду розподілу лежить арифметична прогресія, за аналогією можна спростити розрахунки умовних моментів і для цього виду рядів розподілу.
Відношення і називають умовними варіантами.
Останні, як бачимо, використовують для спрощених методів розрахунку зведених характеристик вибірки шляхом заміни початкових варіант умовними.
Приклад. Необхідно знайти умовні варіанти для дискретного ряду розподілу 50 працівників за середньоденним рівнем зарплати (табл. 37).
Таблиця 37
Дискретний ряд розподілу
Варіанта, Хі | Частота, п |
22,50 | 3 |
26,50 | 8 |
30,50 | 25 |
34,50 | 10 |
38,50 | 4 |
За умовний початок (несправжній нуль -х°) приймаємо варіанту 30,5 (ця варіанта розміщена в середині варіаційного ряду). Різниця між сусідніми (будь-якими) варіантами (і) дорівнює 4. Для інтервального варіаційного ряду - це величина інтервалу.
1 х1 - х0 22,5 - 30,5 2 Умовна варіанта буде дорівнюватиме ' ' 4
Аналогічно розраховуємо інші умовні варіанти: х'2 = -1; х2 = 1; х3 = 1; х'4 = 1;
*5 ~ 2. Як бачимо, одержані значення умовних варіант - це цілі числа, невеликі за обсягом, з якими набагато спрощуються обчислювальні операції в порівнянні з варіантами початкового ряду (22,50; 26,50; 30,50; 34,50; 38,50).
Маючи обчислені значення умовних варіант, можна знайти умовний емпіричний момент, який являє собою початковий момент к -го порядку, обчислений для умовних варіант:
Так, умовний момент першого порядку буде дорівнювати:
Звідси х = ш + Л0.
Отже, щоб знайти середню вибірки, необхідно умовний момент першого порядку помножити на величину інтервалу (і) і до одержаного добутку додати варіанту, прийняту за умовний початок (несправжній нуль).
Від умовних моментів можна перейти до розрахунку початкових
, _ 1 І(хі - х0)*пі _ Мк
~ ~к ^- --к-
моментів розподілу (мк): 1 1 .
Звідси початковий момент к -го порядку дорівнює
Мк = шк х ік
Отже, щоб знайти початковий момент к -го порядку, достатньо умовний момент цього порядку помножити на величину інтервалу в к-ій степені.
Щоб оцінити (дати оцінку) відхилення емпіричного розподілу від нормального, розраховують такі статистичні характеристики, як коефіцієнти асиметрії і гостровершинності - ексцесу. Перший з названих коефіцієнтів характеризує ступінь скошеності варіаційного ряду розподілу щодо його симетрії вправо або вліво.

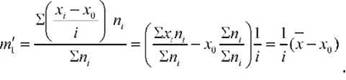
ТЕМА 6. АНАЛІЗ ПОДІБНОСТІ РОЗПОДІЛІВ
§ 6.1. Статистична оцінка параметрів розподілу
§ 6.2. Закони розподілу вибіркових характеристик
6.2.1. Загальне поняття законів розподілу
6.2.2. Нормальний розподіл
6.2.3. Розподіл Стьюдента
6.2.4. Розподіл Хі- квадрат
6.2.5. Розподіл Фішера - Снедекора
МОДУЛЬ 3