Статистика - Опря А.Т. - 6.2.3. Розподіл Стьюдента

При розгляді питання середньої арифметичної у вибірках, які взяті з генеральної сукупності і підпорядковуються закону нормального розподілу, стає очевидним те, що цей розподіл залежить від середнього квадратичного відхилення (^ст2).

У практичних розрахунках значення генерального ^ст2, як правило, невідоме, що призводить до певних розрахункових ускладнень. Ця обставина спонукала англійського статистика В.С.Госсета (він друкувався під псевдонімом Стьюдент) зайнятися пошуком такого розподілу середньої арифметичної, який не залежав би від параметра °.

Поставлена задача Стьюдентом була вирішена у 1908 р. (у цей час він був службовцем на пивоварному заводі у м. Дубліні).

Відкритий закон розподілу підняв на нову сходинку теорію статистичного оцінювання і теорію перевірки статистичних гіпотез. У чому ж виражається розподіл, досліджуваний Стьюдентом? Він

х - X

-="

встановив, що імовірність нормованого відхилення ^а (пізніше Р.Фішер створив більш строгий теоретичний

фундамент: ^п~¹ ) виражається рівнянням:

р(г) = с (1+-?-) ~ ~^{2 2}

п-1

де P(X) - імовірність того, що стандартизована різниця між ~ і ^х має величину "; С - деякий коефіцієнт, який залежить від обсягу вибірки. Величина його становить:

с. , ^

^(п -1) х Г(^)

_{(") f-) '}

де Г v²) і Г v ² ) - гама - функції.

Повна формула закону розподілу нормованого відхилення має вигляд:

ІД) "2 і

Р(') =_П-=-- х (1 + ^) ²

п (п -1) Г (^) ^П-¹

Закону розподілу "-Стьюдента підпорядковуються малі вибірки, які одержані з нормального розподілу сукупностей. Характерною особливістю даного розподілу є те, що ймовірність значення X залежить від двох величин: обсягу вибірки (п) і нормованого відхилення (ґ) . Причому п береться числом ступенів вільності ( уу=п-

1).

При збільшенні чисельності вибіркової сукупності розподіл Стьюдента наближається до нормального:

1

Р(І) =~і= е ²

л/277

У спеціальній літературі є доведення, що при необмеженому зростанні обсягу вибірки розподіл Стьюдента прагне до нормального закону розподілу.

Якщо вибірка достотно мала (п < 15), розподіл імовірностей буде відрізнятися від нормального і тим більше, чим менший обсяг вибірки. Крива розподілу у таких випадках ніби розтягується (рис.15). Із збільшенням обсягу вибірки розподіл Стьюдента досить швидко наближається до нормального, зокрема, при п = 20 він практично не відрізняється від нього.

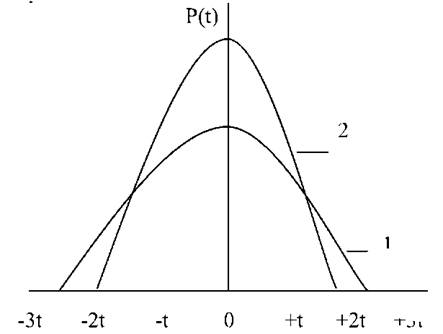
Рис. 17. Розподіл Стьюдента (I) на фоні нормальної кривої (2)

Із сказаного виходить, що розподіл Стьюдента являє собою частковий випадок нормального розподілу і відображає специфіку варіації для нечисленної вибірки, яка розподіляється за нормальним законом розподілу залежно від п .

Показники рівнів імовірності (Р(і)), що розподіляється за законом Стьюдента, дано в стандартній математичній таблиці "Імовірності ґ-розподілу по Стьюденту для малих вибірок (у межах ± ?)" (додаток2). У цій таблиці наведені рівні ймовірностей Р для кожного значення нормованого відхилення ґ при визначеному обсязі вибірки, який береться "числом ступенів вільності". Тому положення про те, що кожному обсягу вибірки відповідає певне значення і, необхідно уточнити. Тут очевидна доцільність формулювання: кожному числу ступенів вільності відповідає і-розподіл. Розглянемо приклад.

Приклад. За результатами вибіркового обстеження 10 сімей підприємств харчової промисловості отримані середні рівні місячної заробітної плати, яка припадає на одного члена сім'ї, грн.: 100, 106, 85, 94, 88, 102, 120, 60, 95, 90.

Спираючись на дані вибірки, необхідно перевірити припущення, що середній розмір зарплати, який припадає на одного члена сім'ї працівників

харчової промисловості (генеральна сукупність), дорівнюватиме 85 грн. (^х).

Ґрунтуючись на припущенні про нормальний характер розподілу досліджуваної ознаки в генеральній сукупності, виконуємо розрахунки:

обчислюємо параметри ^х = 94; °^в =14,9.

Прийнявши ^х = 85, визначаємо числове значення нормованого " ₌ 1^1^ ₌ 94-85^ ₌ 1,91 відхилення ^{а 14,9} .Знаходимо за стандартною таблицею

(додаток 2) імовірність для " = 1,9 і числа ступенів вільності и= 10 - I. Для таких параметрів розрахункове значення ймовірності Р = 0,955. Таким чином, для числового значення величини нормованого відхилення X = 1,91 імовірність Р = 0,955. Тобто, імовірність появи значення X , більшим, ніж одержане при вибірці, буде ^а = I - 0,955 = 0,045, або приблизно один випадок з 20. Імовірність появи ", яке по абсолютною величиною буде більше спостережуваного значення, становитиме ^2а =0,090, тобто приблизно один випадок з 10. Таке значення X слід визнати неістотним. Тому різниця між вибірковою і генеральною середньою не буде перевищувати 9 грн. (94-85).

Якщо визнати вибіркове значення " істотним, а таке припущення можна висунути, оскільки спостережуване значення X мало імовірне, то початкове припущення, зумовлене обчисленням значення X, буде невірним. Подібне міркування приводить до висновку про те, що середній розмір зарплати у розрахунку на одного члена сім'ї працівників досліджуваної галузі 85 грн. є

сумнівним, а різниця між генеральною (^х =85) и вибірковою (^х = 94) середньою легко могла перевищити 9 гривень.

Крім розглянутої вище стандартної таблиці, широке практичне застосування знаходить інша математична таблиця значень критерію X для різних рівнів значимості ^а= 1-Р. Вона дозволяє (при певному рівні ^а) встановити можливі границі випадкових коливань вибіркової середньої (^х), а також знайти довірчий інтервал, який покриває середню арифметичну у генеральній сукупності (додаток 1).

Розглянемо випадок використання стандартної таблиці "Критичні точки розподілу Стьюдента ("-розподіл)" на наступному прикладі.

Внаслідок вибіркового обстеження 20 сільськогосподарських підприємств обласного регіону визначено середній показник вихододнів з розрахунку на одного працюючого, який виявився рівним 250, з середньої помилкою вибірки ^т = ^±5. Потрібно визначити довірчий інтервал випадкових коливань шуканої середньої величини при рівні значимості ^а = 0,05.

У додатку I на перетині графи, яка відповідає ^а= 0,05, і рядку 20 - I =19 (число ступенів вільності) знаходимо значення і = 2,09. Отже, довірчий інтервал дорівнює ^ = ~ ^{± ґт} = ^{250 ± 2,09 х 5} = ^{250 ± 10,45,} або закруглено 250 ± 10.

Таким чином, межі генеральної середньої дорівнюватимуть 240-260, тобто в сільгосппідприємствах обстежуваного обласного регіону середній рівень показника кількості вихододнів з розрахунку на одного працюючого буде знаходитися між 240 і 260. Дане ствердження одержане при порозі ймовірності Р =0,95. Рівень імовірності вибирається залежно від конкретних вимог вирішуваного завдання. В економічних дослідженнях використовують імовірність Р = 0,95 (0,954).

Висловлене раніше положення про те, що при збільшенні обсягу вибірки розподіл Стьюдента наближається до нормального підтверджує порівняння даних двох стандартних таблиць: "Критичні точки розподілу Стьюдента (ґ-розподіл)" (додаток 1) і "Функція нормованого відхилення" (додаток 5). Достатньо розглянути фрагмент з обох таблиць для кількох вибірок, щоб переконатися у сказаному вище висновку (табл. 46).

Таблиця 46

Витяг з стандартної таблиці ^розподілів (додаток 1)

Так, у додатку 5 значенню рівня ймовірності 0,95 відповідає величина 1,96. Аналізуючи дані таблиці 46, бачимо, що при п= 60 розподіл Стьюдента майже не відрізняється від нормального:

2.00 - 1,96 = 0,04.

При невеликому обсязі вибірки ці два види розподілу мають значні чисельні відміни. Наприклад, для п =5 різниця у параметрах становитиме 2,78 - 1,96 = 0,82.

На завершення ще раз зробимо акцент на тому, що параметр

~ - х г^а має розподіл Стьюдента за умови, якщо досліджувана випадкова величина підпорядкована закону нормального розподілу, а середня обчислюється за вибірковими даними незалежних спостережень.

Назвемо також аспекти застосування розподілу Стьюдента.

1) При оцінці параметрів генеральної сукупності за даними малих вибірок (для визначення довірчих інтервалів);

2) При перевірці статистичних гіпотез відносно параметрів генеральної сукупності.