Статистика - Опря А.Т. - 6.2.2. Нормальний розподіл

Закон нормального розподілу, так званий Закон Гаусса, - один з найпоширеніших законів. Це фундаментальний закон у теорії ймовірностей і в її застосуванні. Нормальний розподіл найчастіше зустрічається у вивченні природних і соціально-економічних явищ. Інакше кажучи, більшість статистичних сукупностей у природі і суспільстві підпорядковується закону нормального розподілу. Відповідно можна сказати, що сукупності значної частини великих за обсягом вибірок підпорядковуються закону нормального розподілу. Ті із сукупностей, які відхиляються від нормального розподілу в результаті спеціальних перетворень, можуть бути наближені до нормального. У зв'язку з цим слід пам'ятати, що принципова особливість цього закону стосовно до інших законів розподілу полягає в тому, що він є законом границі, до якої наближаються інші закони розподілу в певних (типових) умовах.

Слід відмітити, що термін "нормальний розподіл" має умовний зміст, як загальноприйнятий у математичній і статистико-математичній літературі термін. Твердження, що та чи інша ознака будь-якого явища підпорядковується закону нормального розподілу, зовсім не означає непохитність норм, ніби притаманних досліджуваному явищу, а віднесення останнього до другого виду закону не означає якусь анормальність даного явища. У цьому розумінні термін "нормальний розподіл" не зовсім вдалий.

Нормальний розподіл (закон Гаусса-Лапласа) є типом безперервного розподілу. Де Муавр (1773, Франція) вивів нормальний закон розподілу ймовірностей. Основні ідеї цього відкриття були використані в теорії помилок вперше К. Гауссом (1809, Німеччина) і А.Лапласом (1812, Франція), які внесли вітчутний теоретичний вклад у розробку самого закону. Зокрема, К.Гаусс у своїх розробках виходив з визнання найбільш імовірним значенням випадкової величини-середню арифметичну. Загальні умови виникнення нормального розподілу встановив А.М.Ляпунов. Ним було доведено, що якщо досліджувана ознака являє собою результат сумарної дії багатьох факторів, кожен з яких мало пов'язаний з більшістю решти, і вплив кожного фактора на кінцевий результат набагато перекривається сумарним впливом всієї решти факторів, то розподіл стає близьким до нормального.

Нормальним називають розподіл імовірностей безперервної випадкової величини, яка має щільність:

_ 1 1 (&#)²

/(х,х,<т) = -^е ^{2 ст2}

де ^х - математичне очікування або середня величина. Як видно, нормальний розподіл визначається двома параметрами: ^х і ° . Щоб задати нормальний розподіл, досить знати математичне очікування, або середню і середнє квадратичне відхилення. Ці дві величини визначають центр групування і форму

кривої на графіку. Графік функції ^{ї(хх,ст)} називається нормальною кривою (крива Гаусса) з параметрами ^х і ^ст (рис. 12).

Крива нормального розподілу має точки перегину при X ± 1. Якщо уявити графічно, то між X=+l і 1=-1 знаходиться 0,683 частини всієї площі кривої (тобто 68,3%). У границях X=+2 і X- 2. знаходяться 0,954 площі (95,4 %), а між X=+3 і X= - 3 - 0,997 частини всієї площі розподілу (99,7%). На рис. 13 проілюстрований характер нормального розподілу з одно-, дво- і трисигмовою границями.

При нормальному розподілі середня арифметична, мода і медіана будуть рівними між собою. Форма нормальної кривої має вид одновершинної симетричної кривої, вітки якої асимптотично наближаються до осі абсцис. Найбільша ордината кривої відповідає ^х = 0 . У цій точці на осі абсцис розміщується чисельне значення ознак, яке дорівнює середній арифметичній, моді і медіані. По обидві сторони від вершини кривої її вітки спадають, змінюючи в певних точках форму випуклості на увігнутість. Ці точки симетричні і відповідають значенням ^{х = ±1,} тобто величинам ознаки, відхилення яких від середньої чисельно дорівнює середньому квадратичному відхиленню. Ордината, що відповідає середній арифметичній, ділить всю площу між кривою і віссю абсцис пополам. Отже, ймовірності появи значень досліджуваної ознаки більших і менших середньої

арифметичної будуть рівні 0,50, тобто ^х,(~^^{х) = 0,50} У

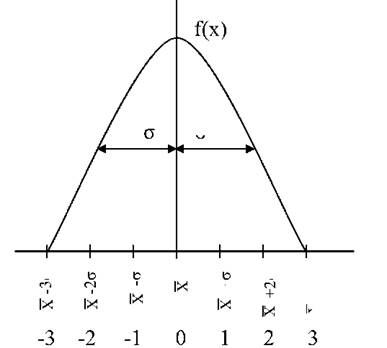
Рис.12. Крива нормального розподілу (крива Гауса)

Форму і положення нормальної кривої зумовлюють значення середньої і середнього квадратичного відхилення. Математично доведено, що зміна величини середньої (математичного очікування) не змінює форми нормальної кривої, а призводить лише до її зміщення вподовж осі абсцис. Крива зрушується вправо, якщо ~ зростає, і вліво, якщо ~ спадає.

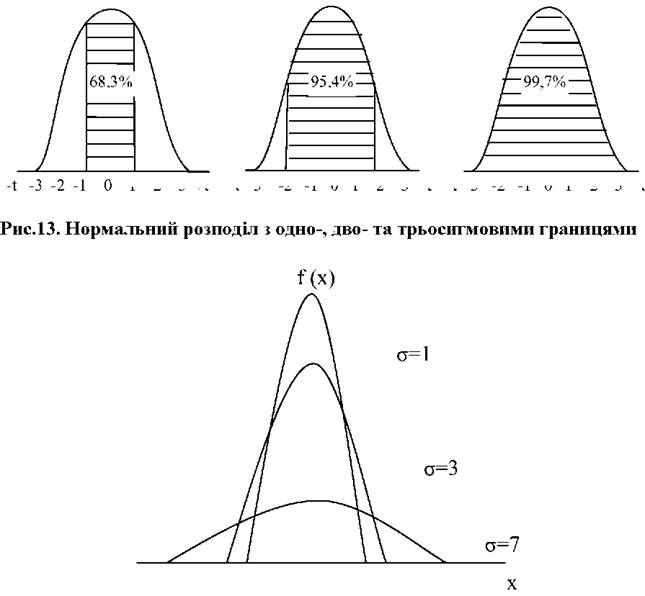
Рис.14. Криві нормального розподілу з різними значеннями параметра о

Про зміну форми графіка нормальної кривої при зміні

середнього квадратичного відхилення можна судити по максимуму

диференціальної функції нормального розподілу, який дорівнює 1

. Як видно, при зростанні величини ° максимальна ордината кривої буде зменшуватися. Отже, крива нормального розподілу буде стискуватися до осі абсцис і приймати більш плосковершинну форму.

І, навпаки, при зменшенні параметра ^ст нормальна крива витягується в додатному напрямку осі ординат, а форма "дзвона" стає більш гостровершиною (рис. 14). Відзначимо, що незалежно від величини параметрів ~ і ^ст площа, обмежена віссю абсцис і кривою, завжди дорівнює одиниці (властивість щільності розподілу). Це наочно ілюструє графік (рис. 13).

Названі вище особливості прояву "нормальності" розподілу дозволяють виділити ряд загальних властивостей, які мають криві нормального розподілу:

1) будь-яка нормальна крива досягає точки максимуму (^х = ^х) ; спадає безперервно вправо і вліво від нього, поступово наближаючись до осі абсцис;

2) будь-яка нормальна крива симетрична по відносно прямої,

паралельної осі ординат і проходить через точку максимуму (^х = ^х);

1

максимальна ордината дорівнює ^^^я;

3) будь-яка нормальна крива має форму "дзвона", має випуклість, яка направлена вверх до точки максимуму. У точках ^х ~° і ^х + ^ствона змінює випуклість, і , чим менше ^а, тим гостріше "дзвін", а чим більше ^а, тим більш похилішою стає вершина "дзвону" (рис.14). Зміна математичного очікування (при незмінній величині

^ст) не призводить до модифікації форми кривої.

При ^х = ⁰ і ° =¹ нормальну криву називають нормованою кривою або нормальним розподілом у канонічному вигляді.

Нормована крива описується наступною формулою:

Побудова нормальної кривої за емпіричними даними здійснюється за формулою:

пі 1 -- "" =---7= ^е

де ^и™ - теоретична частота кожного інтервалу (групи) розподілу; " - сума частот, що дорівнює обсягу сукупності; ' - крок інтервалу;

^ж - відношення довжини кола до його діаметру, яке становить

3,1416;

е - основа натуральних логарифмів, дорівнює 2,71828;

х - X

Друга і третя частини формули ) _є функцією

нормованого відхилення цч), яку можна розрахувати для будь-яких значень X . Таблиці значень цч) звичайно називають "Таблицями ординат нормальної кривої" (додаток 3). При використанні цих функцій робоча формула нормального розподілу набуває простого вигляду:

а

Приклад. Розглянемо випадок побудови нормальної кривої на прикладі даних про розподіл 57 працівників за рівнем денного заробітку (табл. 42). За даними таблиці 42, знаходимо середню арифметичну:

~ ₌ ^ ₌ І6⁵⁴ ₌

57

Розраховуємо середнє квадратичне відхилення:

Для кожної рядка таблиці знаходимо значення нормованого відхилення

^хі ~ ^х | 12 ґ = >-- = -^2- = 1.92

а ^6.25 (дд_Я першого інтервалу і т.д.).

У графі 8 табл. 42 записуємо табличне значення функції Дї) з додатка , наприклад, для першого інтервалу X=1.92 знаходимо "1,9" проти "2" (0.0632).

Для обчислення теоретичних частот, тобто ординат кривої нормального розподілу, обчислюється множник:

* = ^ = 36,5 а 6,25

Усі знайдені табличні значення функції /(ґ) множимо на 36,5. Так, для першого інтервалу одержуємо 0,0632x36,5 = 2,31 тощо. Прийнято нечисленні

частоти (^п' <5) об'єднувати (у нашому прикладі - перших два і останніх два інтервали).

Якщо крайні теоретичні частоти значно відрізняються від нуля, розбіжність між сумами емпіричних і теоретичних частот може виявитися значною.

Графік розподілу емпіричних і теоретичних частот (нормальна крива) за даними розглянутого прикладу показано на рисунку 15.

Розглянемо приклад визначення частот нормального розподілу для випадку, коли в крайніх інтервалах відсутня частота (табл. 43). Тут емпірична

. 2

X - нормоване відхилення, ( ^ст ); ^а - середнє квадратичне відхилення.

частота першого інтервалу дорівнює нулю. Отримана сума неуточнених частот не дорівнює сумі їх емпіричних значень (56 * 57). У цьому випадку розраховується теоретична частота для умовно отриманих значень центра інтервалу, нормованого відхилення і його функції.

У таблиці 43 ці величини обведено прямокутником. При побудові графіка нормальної кривої у таких випадках теоретичну криву продовжують. У розглянутому випадку нормальна крива буде продовжена в бік від'ємних відхилень від середньої, оскільки перша не уточнена частота дорівнює 5. Розрахована теоретична частота (уточнена) для першого інтервалу буде дорівнювати одиниці. По сумі уточнені частоти збігаються з емпіричними

(57=57).

Таблиця 42

Розрахунок частот нормального розподілу (вирівнювання емпіричних частот за нормальним законом)

Таблиця 43

Розрахунок частот нормального розподілу (вирівнювання емпіричних частот по нормальному закону)

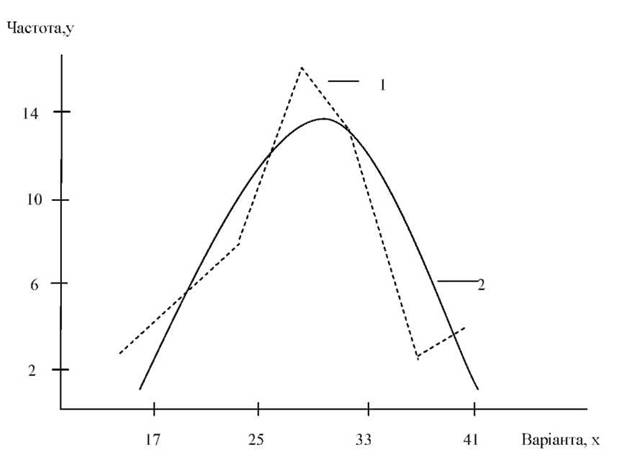
Рис. 15. Емпіричний розподіл (1) і нормальна крива (2)

Криву нормального розподілу по досліджуваній сукупності можна побудувати і іншим способом (на відміну, від розглянутого вище). Так, якщо необхідно мати наближену уяву про відповідності фактичного розподілу нормальному, обчислення здійснюють у такий послідовності. Визначають максимальну ординату, яка відповідає середньому розміру ознаки ), потім, обчисливши середнє квадратичне відхилення, розраховують координати точок кривої нормального розподілу за схемою, викладеною в таблицях 42 і 43. Так, за вихідними і розрахунковими даними таблиці 43 маємо середню ~ = ²⁶ Ця величина середньої збігається з центром четвертого інтервалу (25-27). Отже, частота цього інтервалу "20" може бути прийнята (при побудові графіка) за максимальну ординату). Маючи обчислену дисперсію (^{ст = 2,41}, див. табл. 43), розраховуємо значення координат всіх необхідних точок кривої нормального розподілу (табл. 44, 45). За отриманими координатами креслимо нормальну криву (рис. 16), прийнявши за максимальну ординату частоту четвертого інтервалу.

Узгодженість емпіричного розподілу з нормальним може бути встановлена також шляхом спрощених розрахунків. Так, якщо відношення показника міри асиметрії (^) до своєї середнєквадрати-чної помилки ^ша' або відношення показника ексцесу (Е^х) до своєї середнєквадратичної помилки^т& перевищує за абсолютною величиною число "3", робиться висновок про невідповідність емпіричного розподілу характеру нормального розподілу (тобто,

Ац Ех

якщо ™^А >3 або ^ше' >3).

Є й інші, нетрудомісткі прийоми встановлення "нормальності" розподілу: а) порівняння середньої арифметичної з модою і медіаною; б) використання чисел Вестергарда; в) застосування графічного способу за допомогою напівлогарифмічної сітки Турбіна; г) обчислення спеціальних критеріїв узгодження та ін.

Таблиця 44

Координати 7 точок кривої нормального розподілу

Таблиця 45

Обчислення координат точок кривої нормального розподілу

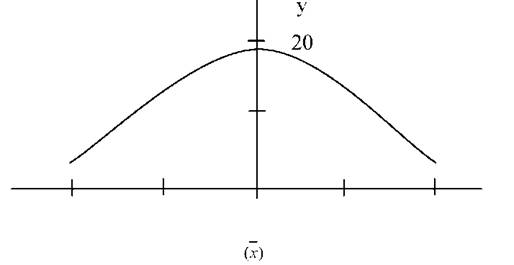
Рис .16. Крива нормального розподілу, побудована по семи точках

На практиці при дослідженні сукупності на предмет узгодження її розподілу з нормальним часто користуються "правилом ^3сг".

Математично доведено ймовірність того, що відхилення від середньої за абсолютною величиною буде менше потрійного середнього квадратичного відхилення, дорівнюватиме 0,9973, тобто, ймовірність того, що абсолютна величина відхилення перевищує потрійне середнє квадратичне відхилення, дорівнює 0,0027 або дуже мала. Виходячи з принципу неможливості малоймовірних подій, можна вважати практично неможливим "випадок перевищення" ^3ст. Якщо випадкова величина розподілена нормально, то абсолютна величина її відхилення від математичного очікування (від середньої) не перевищує потрійного середнього квадратичного відхилення.

У практичних розрахунках діють таким чином. Якщо при невідомому характері розподілу досліджуваної випадкової величини розраховане значення відхилення від середньої виявиться менше значення 3^СТ, то є підстави вважати, що досліджувана ознака розподілена нормально. Якщо ж вказаний параметр перевищить числове значення 3^СТ, можна вважати, що розподіл досліджуваної величини не узгоджується з нормальним розподілом.

Обчислення теоретичних частот для досліджуваного емпіричного ряду розподілу прийнято називати вирівнюванням емпіричних кривих по нормальному (або будь-якому іншому) закону розподілу. Цей процес має важливе як теоретичне, так практичне значення. Вирівнювання емпіричних даних розкриває закономірність в їх розподілі, яка може бути завуальована випадковою формою свого прояву. Встановлену таким чином закономірність можна використовувати для вирішення ряду практичних завдань.

З розподілом, близьким до нормального, дослідник зустрічається в різних сферах науки і областях практичної діяльності людини. В економіці такого роду розподіли зустрічаються рідше, ніж, скажімо, у техніці або біології. Зумовлено це самою природою соціально-економічних явищ, які характеризуються великою складністю взаємозалежних і взаємопов'язаних факторів, а також наявністю ряду умов, які обмежують вільну "гру" випадків. Але економіст повинен звертатися до нормального розподілу, аналізуючи будову емпіричних розподілів, як до деякого еталону. Таке порівняння дозволяє з'ясувати характер тих внутрішніх умов, які визначають дану фігуру розподілу.

Проникнення сфери статистичних досліджень в область соціально-економічних явищ дало змогу розкрити існування великої кількості різного типу кривих розподілу. Однак не треба вважати, що теоретична концепція кривої нормального розподілу взагалі мало придатна у статистико-математичному аналізі такого типу явищ. Вона може бути не завжди прийнятна в аналізі конкретного статистичного розподілу, але в області теорії і практики вибіркового методу дослідження має першочергове значення.

Назвемо основні аспекти застосування нормального розподілу у статистико-математичному аналізі.

1. Для визначення ймовірності конкретного значення ознаки. Це необхідно при перевірці гіпотез про відповідність того чи іншого емпіричного розподілу нормальному.

2. При оцінці ряду параметрів, приміром, середніх, методом максимальної правдоподібності. Суть його полягає у визначенні такого закону, якому підпорядковується сукупність. Визначається та оцінка, яка дає максимальні значення. Краще наближення до параметрів генеральної сукупності дає відношення:

₁

у=-₂=^{е 2}

3. Для визначення ймовірності вибіркових середніх відносно генеральних середніх.

4. При визначенні довірчого інтервалу, в якому знаходиться наближене значення характеристик генеральної сукупності.