Теорія статистики - Мармоза А.Т. - 6.2. Помилки вибірки

Між показниками вибіркової сукупності і шуканими показниками (параметрами) генеральної сукупності, як правило, існують деякі розбіжності, які називають помилками вибірки. Загальна помилка вибіркової характеристики складається з помилок двох родів: помилок реєстрації і помилок репрезентативності.

Помилки реєстрації властиві будь-якому статистичному спостереженню і поява їх може бути викликана неуважністю реєстратора, неточністю підрахунків, недосконалістю вимірювальних приладів тощо.

Помилки репрезентативності притаманні тільки вибірковому спостереженню і зумовлені самою його природою оскільки як би ретельно і правильно не проводився відбір одиниць середні і відносні показники вибіркової сукупності завжди будуть якоюсь мірою відрізнятися від відповідних показників генеральної сукупності.

Розрізняють систематичні та випадкові помилки репрезентативності. Систематичні помилки репрезентативності - це неточності, які виникають внаслідок недотримання умов відбору одиниць у вибіркову сукупність, не надання рівної можливості кожній одиниці генеральної сукупності потрапити у вибірку. Випадкові помилки репрезентативності - це похибки, які виникають внаслідок того, що вибіркова сукупність точно не відтворює характеристики генеральної сукупності (середню, частку, дисперсію та ін.) в силу несуцільного характеру обстеження.

При дотриманні принципу випадкового відбору розмір помилки вибірки залежить насамперед від чисельності вибірки. Чим більше чисельність вибірки при інших рівних умовах, тим меншою є величина помилки вибірки. При великій чисельності вибірки виразніше проявляється дія закону великих чисел, згідно з яким: з імовірністю, скільки завгодно близькою до одиниці, можна стверджувати, що при досить великому обсязі вибірки та обмеженій дисперсії вибіркові характеристики (середня, частка) будуть скільки завгодно мало відрізнятися від відповідних генеральних характеристик.

Розміри помилки вибірки також безпосередньо пов'язані зі ступенем варіювання досліджуваної ознаки, а ступінь варіювання, як зазначалося вище, в статистиці характеризується розміром дисперсії (розсіяння): чим менша дисперсія, тим меншою є помилка вибірки, тим надійніші статистичні висновки. Тому на практиці дисперсію ототожнюють з помилкою вибірки.

Оскільки параметр генеральної сукупності є шукана величина і він невідомий, потрібно орієнтуватися не на конкретну помилку, а середню з усіх можливих вибірок.

Якщо з генеральної сукупності відібрати кілька вибіркових сукупностей, то кожна із отриманих вибірок дасть різне значення конкретної помилки.

Середня квадратична величина /і, обчислена з усіх можливих значень конкретних помилок (є;) становитиме:

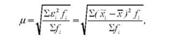
де *і - вибіркові середні; х - генеральна середня; )] - чисельність вибірок з величиною є1 = ~сі - х.

Середнє квадратичне відхилення вибіркових середніх від генеральної середньої називають середньою помилкою вибірки.

Залежність величини помилки вибірки від її чисельності та від ступеня варіювання ознаки знаходить вираження у формулі середньої помилки вибірки /і.

Квадрат середньої помилки (дисперсія вибіркових середніх) прямо пропорційний дисперсії Сто і обернено пропорційний чисельності вибірки п:

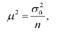
де - дисперсія ознаки у генеральній сукупності.

Звідси середню помилку в загальному вигляді визначають за формулою:

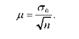
Отже, визначивши за вибіркою середнє квадратичне відхилення, можна встановити значення середньої помилки вибірки, величина якої, як випливає з формули, тим більша, чим більшою є варіація випадкової величини і тим менша, чим більшою є чисельність вибірки.

Тому з мірою зростання обсягу вибірки розмір середньої помилки зменшується. Якщо, наприклад, потрібно зменшити середню помилку вибірки в два рази, то чисельність вибірки слід збільшити в чотири рази, якщо треба зменшити помилку вибірки в три рази, то обсяг вибірки слід збільшити в дев'ять разів і т. д.

У практичних розрахунках застосовують дві формули середньої помилки вибірки: для середньої і для частки.

При вибірковому вивченні середніх показників формула середньої помилки така:

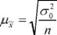
При вивченні відносних показників (часток ознак) формула середньої помилки має вигляд:

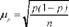
дер - частка ознаки в генеральній сукупності.

Застосування наведених формул середньої помилки передбачає, що відомі генеральна дисперсія та генеральна частка. Проте в дійсності ці показники невідомі і обчислити їх неможливо через відсутність даних щодо генеральної сукупності. Тому виникає потреба заміни генеральної дисперсії та генеральної частки іншими, близькими до них, величинами.

В математичній статистиці доведено, що такими величинами можуть бути вибіркова дисперсія(ст ) та вибіркова частка (со).

З урахуванням сказаного формули середньої помилки можуть бути записані так:

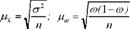
Ці формули дають змогу визначити середню помилку при повторній вибірці. Застосування простої випадкової повторної вибірки у практиці є обмеженим. Насамперед практично недоцільно, а інколи неможливо повторне обстеження тих самих одиниць. Застосування безповторного відбору замість повторного диктується також вимогою підвищення ступеня точності і надійності вибірки. Тому на практиці найчастіше використовують спосіб безповторного випадкового відбору. За цим способом відбору одиниця сукупності, що відібрана у вибірку, в подальшому відборі участі не бере. Одиниці відбирають із генеральної сукупності, зменшеної на кількість раніше відібраних одиниць. Тому в зв'язку із зміною чисельності генеральної сукупності після кожного відбору та ймовірності відбору для одиниць, що залишились, у формули середньої помилки вибірки вводиться поправочний множник

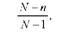
де N - чисельність генеральної сукупності; п - чисельність вибірки. При досить великому значенні N можна одиницею в знаменнику знехтувати. Тоді

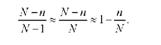
Відтак формули середньої помилки вибірки для безповторного відбору для середньої і для частки відповідно мають вигляд:

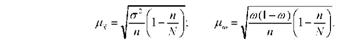
1 - п

Оскільки п завжди менше М, то додатковий множник завжди менше одиниці. Отже, абсолютне значення помилки вибірки при безповторному відборі завжди менше, чим при повторному.

1 п

Якщо чисельність вибірки досить велика, то величина 1 ^ близька до одиниці, а тому нею можна знехтувати. Тоді середню помилку випадкового безповторного відбору визначають за формулою власне випадкової повторної вибірки.

Розрахуємо для нашого прикладу середню помилку для урожайності і для частки ділянок з урожайністю 25 ц/га і більше.

Середня помилка вибірки

а) середньої урожайності ячменю

Середня урожайність ячменю в генеральній сукупності х -М^ = 25,1 ± 0,12 ц/га, тобто знаходиться в межах від 24,98 до 25,22 ц/га.

Частка ділянок з урожайністю 25 ц/га і більше в генеральній сукупності р

= т-^Р = 0,80 ± 0,07, тобто знаходиться в межах від 73 до 87%.

Середня помилка вибірки показує можливі відхилення характеристик вибіркової сукупності від характеристик генеральної сукупності. Разом з тим при проведенні вибіркового спостереження перед дослідниками часто стоїть завдання розрахунку не тільки середньої помилки, але і визначення граничної можливої помилки вибірки. Знаючи середню помилку, можна визначити межі, за які не вийде величина помилки вибірки. Однак стверджувати, що ці відхилення не перевищать заданої величини, можна не з абсолютною вірогідністю, а лише з певним ступенем імовірності. Рівень імовірності, що приймається при визначенні можливих меж, в яких містяться значення параметрів генеральної сукупності, називається довірчим рівнем імовірності.

Довірча імовірність - це досить висока і, така, що практично вважається здійсненою в кожному конкретному випадку, імовірність, що гарантує отримання надійних статистичних висновків. Позначимо її через Р, а імовірність перевищити цей рівень - а. Отже, а =1 - Р. Імовірність а називають рівнем значущості (істотності), який характеризує відносне число помилкових висновків у загальному числі висновків і визначається як різниця між одиницею і довірчою імовірністю, що приймається.

Рівень довірчої імовірності встановлює дослідник виходячи зі ступеня відповідальності і характеру завдань, що розв'язуються. У статистичних дослідах в економіці найчастіше приймається рівень довірчої імовірності Р = 0,95; Р = 0,99 (відповідно рівень значущості а = 0,05; а = 0,01) рідше Р = 0,999. Наприклад, довірча імовірність Р = 0,99 означає, що помилка оцінки у 99 випадках із 100 не перевищить встановленої величини і тільки в одному випадку із 100 може досягти обчисленого значення, або перевищити його.

Помилка вибірки, що обчислена із заданим ступенем надійної імовірності, називається граничною помилкою вибірки Єр.

Розглянемо, як встановлюється величина можливої граничної помилки вибірки. Величина єр пов'язана з нормованим відхиленням і, яке визначається як відношення граничної помилки вибірки єр до середньої помилки /і:

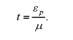
Для зручності розрахунків відхилення випадкової величини від її середнього значення звичайно виражають в одиницях середнього квадратичного відхилення. Вираз

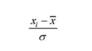
називають нормованим відхиленням. В статистичній літературі і ще називають коефіцієнтом довіри, або коефіцієнтом кратності середньої помилки вибірки.

Так, нормоване відхилення для вибіркової середньої можна визначити за формулою:

і _є_р_

Із виразу 1 можна знайти можливу граничну помилку, вибірки

єр = і/л.

Підставивши замість р. її значення, наведемо формули граничних помилок вибірки для середньої і для частки при безповторному випадковому відборі:

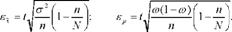
Отже, гранична помилка вибірки залежить від величини середньої помилки і нормованого відхилення і дорівнює ± кратному числу середніх помилок вибірки.

Середня і гранична помилки вибірки - величини іменовані і виражаються в тих самих одиницях, що й середня арифметична і середнє квадратичне відхилення.

Нормоване відхилення функціонально зв'язано з імовірністю. Для знаходження значень і складені спеціальні таблиці (дод.2), за якими можна знайти значення і при заданому рівні довірчої імовірності і значення імовірності при відомому і.

Наведемо значення і та відповідні до них імовірності для вибірок з чисельністю п > 30, що найчастіше використовується в практичних розрахунках:

Отже, при і = 1 імовірність відхилення вибіркових характеристик від генеральних на величину однократної середньої помилки вибірки дорівнює 0,6827. Це означає, що в середньому із кожної 1000 вибірок 683 дадуть узагальнені характеристики, які відрізнятимуться від генеральних узагальнених характеристик не більше, чим на величину однократної середньої помилки. При і = 2 імовірність дорівнює 0,9545. Це означає, що із кожної 1000 вибірок 954 дадуть узагальнені характеристики, які відрізнятимуться від генеральних узагальнених характеристик не більш ніж на двократну середню помилку вибірки і т.д.

Однак в зв'язку з тим, що, як правило, проводиться тільки одна вибірка, то ми кажемо, що, наприклад, із імовірністю 0,9545 можна гарантувати, що розміри граничної помилки не перевищать двократну середню помилку вибірки.

Математично доведено, що відношення помилки вибірки до середньої помилки, як правило, не перевищує ± 3д при досить великій чисельності п, незважаючи на те, що помилка вибірки може набувати будь-які значення. Іншими словами можна сказати, що при досить високій імовірності судження (Р = 0,9973) гранична помилка вибірки, як правило, не перевищує трьох середніх помилок вибірки. Тому величину Єр = 3д можна прийняти за межу можливої помилки вибірки.

Визначимо для нашого прикладу граничну помилку вибірки для середньої урожайності і для частки ділянок з урожайністю 25 ц/га і більше. Довірчий рівень імовірності приймемо рівним Р = 0,9545. За таблицею (дод.2) знайдемо значення і = 2. Середні помилки вибірки для урожайності і частки ділянок з урожайністю 25 ц/га і більше були знайдені раніше і відповідно становили: Ц~ = ±0,12 ц/га; МР = ± 0,07.

Гранична помилка середньої урожайності ячменю:

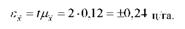
Отже, різниця між вибірковою середньою урожайністю і генеральною середньою буде не більше 0,24 ц/га. Межі середньої урожайності в генеральній сукупності: х = х ±є~ = 25,1 + 0,24, тобто від 24,86 до 25,34 ц/га.

Гранична помилка частки ділянок з урожайністю 25 ц/га і більше:

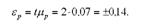
Отже, гранична помилка у визначенні частки ділянок з урожайністю 25 ц/га і більше не перевищить 14%, тобто питома вага ділянок із зазначеною урожайністю в генеральній сукупності знаходиться в межах: р = а> ± єр = 0,80 ± 0,14, тобто від 66 до 94%.