Теорія статистики - Мармоза А.Т. - 9.4. Криволінійна кореляція

Дослідження форми зв'язку інколи зумовлює потребу використання нелінійних (криволінійних) рівнянь регресії. Це пояснюється тим, що взаємодія між ознаками, що характеризують окремі явища і процеси, нерідко має більш складний характер, ніж просто пропорційні залежності.

Характерною особливістю цього зв'язку є те, що рівномірна зміна однієї ознаки супроводжується нерівномірною зміною (збільшенням або зменшенням) значення іншої ознаки.

Нелінійні форми зв'язку притаманні багатьом процесам у сільському господарстві. Так, ріст і розвиток рослин, накопичення ними продуктивної маси, як правило, в часі розвивається нелінійно. Відомо також, що якщо грунти насичені вологою більше певної норми, то урожайність сільськогосподарських культур починає знижуватися. Продуктивність корів залежно від числа отелів (віку корів) спочатку має тенденцію до зростання, досягаючи максимума у 5-7 отелі, а потім починає закономірно знижуватися.

При дослідженні криволінійних зв'язків, так само як і при вивченні лінійних зв'язків, принципове значення має вибір форми і рівняння зв'язку, яке найточніше відобразить наявний зв'язок. Для розв'язання цього завдання використовуються ті самі прийоми, що й при обґрунтуванні лінійного зв'язку. При цьому особлива увага належить графічному методу.

Криволінійні форми зв'язку досить різноманітні. В статистичному аналізі найчастіше використовують параболу другого порядку, гіперболу і степеневу функцію.

При криволінійній залежності система рівнянь будується так само, як і для лінійного зв'язку: вихідне рівняння множиться на коефіцієнти при невідомих і добутки підсумовуються почленно. Так, система рівнянь для параболи другого порядку

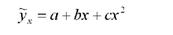
має вигляд:

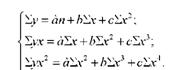
Однією з особливостей параболи другого порядку є те, що вона завжди має точку перегину (критичну точку), яка характеризує оптимальний варіант розміру величини результативної ознаки і змінює свій напрям тільки один раз. Якщо в рівнянні параметр а1 виражений додатним числом, а параметр -а2 від'ємним, то крива змінює напрям із зростання на зниження.

Система рівнянь для гіперболи

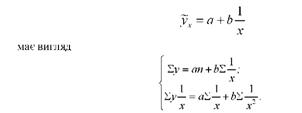
Формули, які випливають із розв'язання цієї системи рівнянь, для визначення параметрів гіперболи мають вигляд:

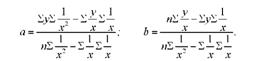
Щоб полегшити обчислення параметрів рівнянь регресії способом найменших квадратів при криволінійній залежності вибране рівняння регресії доцільно звести до лінійного вигляду відповідними перетвореннями.

Процес перетворень нелінійних рівнянь регресії в лінійні називають лінеаризацією.

Покажемо на прикладі трьох нелінійних функцій, найчастіше застосовуваних при вивченні взаємозв'язків, перетворення до лінійного вигляду.

_{~ - ь}

^{1. Гіперболу У* ~ а + х зводять до лінійного вигляду замінивши X}

_ 1

новою змінною (її зворотним значенням 2 ~ х );

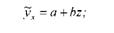
2. Параболу другого порядку ~х - а +Ьх +сх перетворюють замінивши квадрат значень факторної ознаки (г = х2). Одержимо лінійну функцію з двох змінних:

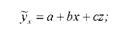
~ _ ь

3. Степеневу Ух ~ ах зводять до лінійного вигляду логарифмуванням

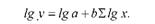
Подальші розрахунки аналогічні розрахункам лінійної функції. Система рівнянь має вигляд :

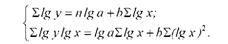
Формули для визначення параметрів степеневої функції

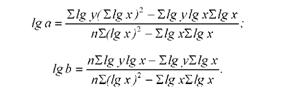
На відміну від прямолінійної залежності коефіцієнти регресії криволінійної регресії не можна інтерпретувати однозначно, так як швидкість зміни результативної ознаки при різному значенні фактора буде неоднаковою. Наприклад, якщо залежність добових надоїв від віку корів, яка характеризується тим, що із зміною віку спочатку продуктивність зростає, а потім поступово знижується, виразити рівнянням параболи другого порядку

Ух = а + Ьх + сх , то коефіцієнт а1 покаже швидкість приросту продуктивності корів, а а2 - її уповільнення.

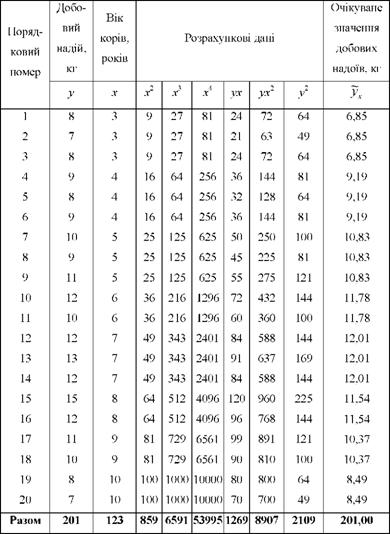
Порядок визначення показників зв'язку при криволінійній залежності розглянемо на такому прикладі (табл. 9.2).

Таблиця 9.2. Дані для розрахунку показників кореляційного зв'язку

Для визначення форми зв'язку між добовими надоями (у) і віком корів (*) побудуємо графік - кореляційне поле (рис. 9.2).

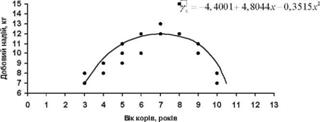
Рис. 9.2. Кореляційне поле залежності добових надоїв від віку корів

З графіка видно, що між добовим надоєм і віком корів зв'язок нелінійний. Добовий надій зростає у міру роздоювання до 6-7 отелення, а потім знижується. Розташування точок на кореляційному полі показує, що зв'язок між надоєм і віком корів можна виразити рівнянням параболи другого порядку:

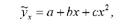
де Ух - добовий надій, кг; х - вік корів, років; а, Ь, с - параметри рівняння.

Для визначення параметрів рівняння регресії а, Ь, с складемо систему рівнянь, для чого послідовно перемножимо всі члени вихідного рівняння на коефіцієнти при невідомих, а одержані добутки підсумуємо:

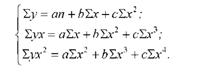
Усі потрібні для розв'язання системи нормальних рівнянь дані (Еу; Ех; Ех2; Ех; Ех4; Еух; Еух2; 2у2) розрахуємо в табл. 9.2. Підставимо одержані дані в систему рівнянь:

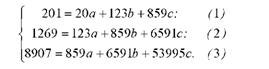
Розв'яжемо систему рівнянь і знайдемо коефіцієнти регресії а, Ь, с: а) поділимо всі члени рівняння на коефіцієнти при а (перше на 20, друге - на 123, третє - на 859):

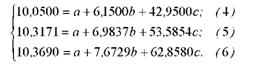
б) віднімемо з 5-го рівняння 4-е і із 6-го рівняння 5-е, в результаті одержимо систему рівнянь з двома невідомими:

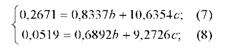
в) поділимо обидва рівняння на коефіцієнти при Ь:

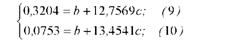
г) віднімемо з 9-го рівняння 10-е: 0,2451 = - 0,6972 с,

звідси с = - 0,3515;

д) підставимо значення с в рівняння 9 і знайдемо коефіцієнт регресії Ь:

0,3204 = Ь + 12,7569 o (- 0,3515) ; Ь = 4,8044;

е) визначимо коефіцієнт регресії а, підставивши значення Ь і с в перше рівняння:

201 = 20а = + 123 o 4,8044 + 859 (- 0,3515); а = - 4,4001.

Перевіримо правильність обчислення коефіцієнтів регресії за такою формулою:

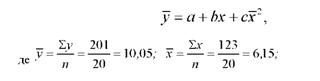
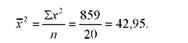
10,05 = - 4,4001 + 4,8044 o 6,15 + (- 0,3515) o 42,95 = 10,05. Отже, рівняння регресії, яке характеризує зв'язок між добовим надоєм і віком корів, має вигляд:

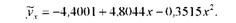
Коефіцієнт регресії Ь = 4,8044 показує, що у міру зростання віку корів

до 7 років (див. графік і очікуване значення надоїв - Ух ) добові надої збільшуються на 4,8044 кг, а потім із збільшенням віку продуктивність корів зменшується. Про це свідчить коефіцієнт регресії с = - 0,3515 кг, який показує уповільнення приростів продуктивності корів.

Оптимальне значення фактора можна розрахувати за формулою

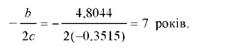
Визначимо очікувані (розрахункові) значення добових надоїв для різного віку корів (Ух ).

Для цього в рівняння регресії замість х (вік корів) підставимо його конкретні значення х = 3, 4, 5, ...10. Так, очікуване значення добового надою для корів у віці 3-х років становить

~х=3 = -4,4001 + 4,8044 o 3 - 0,3515 o 32 = 6,85 кг;

Для корів у віці 4-х років

ух = 4 =-4,4001 + 4,8044 o 4 - 0,3515 o 4 2 = 9,19 кг і т.д.

Результати розрахунків запишемо в останню колонку табл. 9.2. Перевіримо правильність розрахунків:

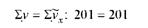
За очікуваними значеннями добових надоїв на рис. 9.2 побудуємо теоретичну лінів регресії.

Особливе значення у вивченні взаємозв'язків між ознаками в економіці належить багатофакторному кореляційно-регресійному аналізу, при якому визначається залежність результативної ознаки від кількох факторів одночасно.

Використання ЕОМ і типових програм кореляційно-регресійного аналізу дає змогу розв'язувати кореляційні моделі різних залежностей і вибрати з цієї множини таке рівняння, яке найточніше описує ступінь наближення фактичних даних до теоретичних і відповідно дає найменшу суму квадратів відхилень фактичних даних від розрахованих за рівнянням зв'язку.

Багатофакторний кореляційно-регресійний аналіз може бути застосований для:

1) розрахунку очікуваних (теоретичних) значень результативної ознаки;

2) зіставлення і оцінки фактичного і розрахункового значень результативної ознаки;

3) порівняльного аналізу різних сукупностей;

4) об'єктивної оцінки результатів роботи підприємств;

5) виявлення резервів виробництва;

6) розроблення нормативів;

7) прогнозування суспільних явищ тощо.

Парна кореляція, в силу того, що разом з досліджуваним фактором на результативну ознаку впливають й інші фактори не завжди дає правильне уявлення про зв'язок між результативною і факторною ознакою (перебільшує або применшує міру залежності). Перевага багатофакторного кореляційно-регресійного аналізу порівняно з простою кореляцією полягає в тому, що він дає змогу оцінити ступінь впливу на результативну ознаку кожного з включених у модель (рівняння) факторів при фіксованому положенні (звичайно на середньому рівні) решти факторів.

Методологія множинної кореляції ґрунтується на загальних принципах кореляційного аналізу. Водночас в ній ускладнюється змістовний аналіз, зростає складність математичного апарату.

При формуванні множинної кореляційної моделі необхідно враховувати ряд обмежень, пов'язаних з відбором, кількістю і взаємозв'язком факторів, вибором форми зв'язку (рівняння регресії).

Відбір найістотніших факторів до кореляційної моделі є одним з найбільш важливіших і принципових завдань багатофакторного кореляційно-регресійного аналізу. Природно, що всі фактори, які впливають на досліджувану результативну ознаку, до рівняння регресії включити не можна. З усього комплексу таких факторів необхідно відібрати найбільш важливі, істотні. Захоплення великою кількістю факторів при відносно невеликій чисельності сукупності може призвести до неякісних результатів. Крім того, із збільшенням в рівнянні регресії кількості параметрів значно утруднюється інтерпретація одержаних результатів.

Велику роль у відборі факторів відіграють завчасно побудовані і проаналізовані факторні групування. Дуже важливого значення тут набувають комбінаційні групування, які дозволяють визначити вплив на результативну ознаку фактора, що цікавить дослідника, при фіксованих значеннях інших факторів. Можна зробити безперечний висновок про те, що статистичні групування становлять основу для кореляційного і дисперсійного аналізу і найбільшої ефективності останні досягають в поєднанні з методом групувань.

Практичні розрахунки показують, що для забезпечення стійкості параметрів рівняння зв'язку, кількість факторів. включених до моделі, має бути в 6 - 8 разів меншою від чисельності досліджуваної сукупності. При цьому сукупність, з якої відбирають фактори, повинна бути якісно однорідною.

Відбираючи фактори, потрібно виключати ті, що взаємно дублюють один одного і перебувають у функціональному зв'язку. Функціональний або близький до нього зв'язок між самими факторами вказує на мультиколінеарність (для двох - колінеарність). Наявність мультиколінеарності свідчить про те, що ці фактори відображають ту саму сторону впливу на результативну ознаку.

При високій корельованості факторів (тіснота зв'язку між двома факторами перевищує г > 0,8) вплив одного з них акумулює і вплив другого. Одержані при цьому кореляційні моделі стають нестійкими.

При формуванні кореляційної моделі до неї потрібно включити один з цих факторів, який істотніше впливає на результативну ознаку. При мультіколінеарності включення до кореляційної моделі взаємопов'язаних факторів можливе тоді, коли тіснота зв'язку між ними менша, ніж тіснота зв'язку результативної ознаки з кожним фактором. Потрібно, щоб кореляційна модель містила незалежні і такі, що не дублюють один одного, фактори. Небажаним є включення до однієї моделі часткових і загальних факторів. Повністю слід виключити фактори, функціонально пов'язані з результативною ознакою.

Важкою і складною проблемою побудови рівняння множинної регресії є також вибір функції зв'язку, тобто вибір математичного рівняння, яке найповніше проявляє характер взаємозв'язку між результативною ознакою і включеними до рівняння регресії факторами.

Одна із складностей полягає у взаємозв'язку і взаємодії факторів між собою та з результативною ознакою. Тому звичайні прийоми, використовувані при виборі форми зв'язку при парній кореляції (графічний та ін.) тут мало прийнятні.

Вибір рівняння регресії може спиратися на положення теорії досліджуваного явища або практичний досвід попередніх досліджень. Якщо таких даних немає, то допомогти у вирішенні цього питання може побудова комбінаційних групувань, таблиць розподілу чисельностей, експертні оцінки, вивчення парних зв'язків між результативною ознакою і кожним фактором, графіки, перебирання функцій різних типів (при розв'язанні задач на ЕОМ), послідовний перехід від лінійних рівнянь зв'язку до більш складних видів тощо.

Виконання усіх цих прийомів пов'язане із значною кількістю зайвих підрахунків. Тому, приймаючи до уваги, що кореляційні зв'язки в більшості випадків відображаються функціями лінійного типу або степеневими, які шляхом логарифмування або заміни змінних можна звести до лінійного вигляду, рівняння множинної регресії можна будувати у лінійній формі. При п змінних лінійне рівняння має вигляд:

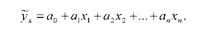
де Ух - залежна змінна (результативна ознака); Хі - незалежні змінні (фактори);

а0 - початок відліку, який економічного смислу немає;

й,2,..., ап - коефіцієнти регресії.

Рівняння, за допомогою якого виражається кореляційний зв'язок між кількома ознаками називають рівнянням множинної регресії. Параметри рівняння регресії, так само як і у випадку парної кореляції, знаходять способом найменших квадратів.

Коефіцієнти множинної регресії показують ступінь середньої зміни результативної ознаки при зміні відповідної факторної ознаки на одиницю (одне своє значення) за умови, що всі інші фактори, які включені до рівняння регресії, залишаються постійними (фіксованими) на одному (звичайно середньому) рівні.

Коефіцієнти множинної регресії, які характеризують зв'язок між результативною ознакою і фактором при фіксованому значенні інших факторів, називаються коефіцієнтами чистої регресії, а коефіцієнти парної регресії - коефіцієнтами повної регресії.

Коефіцієнти чистої регресії, що мають різний фізичний смисл і одиниці вимірювання не дають чіткого уявлення про те, які саме фактори найістотніше впливають на результативну ознаку. Крім того, величина коефіцієнтів регресії залежить від ступеня варіації ознаки.

Щоб привести коефіцієнти чистої регресії до порівнянного вигляду, їх виражають у стандартизованій формі у вигляді коефіцієнтів еластичності (Е) і бета-коефіцієнтів (р).

Коефіцієнти еластичності показують, на скільки процентів змінюється величина результативної ознаки при зміні відповідного фактора на один процент при фіксованому значенні інших факторів.

Коефіцієнти еластичності і коефіцієнти чистої регресії зв'язані між собою таким відношенням:

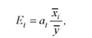
де а,- - коефіцієнт чистої регресії при г'-му факторі;

х, і у - середні значення відповідно г'-го фактора і результативної ознаки.

Бета-коефіцієнти показують, на скільки середньоквадратичних відхилень &у зміниться результативна ознака при зміні відповідного фактора на одне значення середньоквадратичного відхилення &х (при постійності інших факторів, включених до рівняння регресії).

Бета-коефіцієнти обчислюються за формулою:

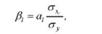
де а,- - коефіцієнт чистої регресії при г'-му факторі;

і °'у - середні квадратичні відхилення відповідно по г'-му фактору і результативній ознаці.

З наведеної формули випливає, що бета-коефіцієнти мають той самий знак (плюс. мінус), що й коефіцієнти чистої регресії.

По суті бета-коефіцієнти характеризують фактори, у розвитку яких приховуються найбільші резерви поліпшення результативної ознаки.

При парному лінійному зв'язку коефіцієнт кореляції являє собою бета-коефіцієнт:

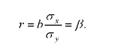
Як зазначалося вище, коефіцієнт множинної детермінації (К2) показує, яка частина загальної варіації результативної ознаки визначається варіацією факторів, включених до кореляційної моделі. Щоб визначити частку впливу кожного фактора у загальній варіації, треба коефіцієнт множинної детермінації розкласти на складові частини:

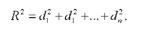
де - коефіцієнти окремого визначення, які можна знайти за формулою:

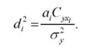
де а,- - коефіцієнти чистої регресії;

~у - дисперсія результативної ознаки;

СухІ - спряжена варіація результативної ознаки і однієї з факторних ознак.

Величину Сухі визначають за формулою:

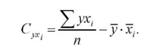
Розкладання загального обсягу варіації результативної ознаки на складові частини можна здійснити й іншим способом. Для цього потрібно знайти добуток парних коефіцієнтів кореляції ( ух, ) на відповідні бета-коефіцієнти ( Рі ), а одержані по всіх факторах результати підсумувати

Щоб визначити частку впливу кожного фактора в сумарному впливі факторів, включених до рівняння регресії, розраховують коефіцієнти окремого визначення (^ ):

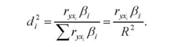
Якщо потрібно частку впливу кожного фактора визначити у процентах, то знайдені коефіцієнти множать на сто процентів.

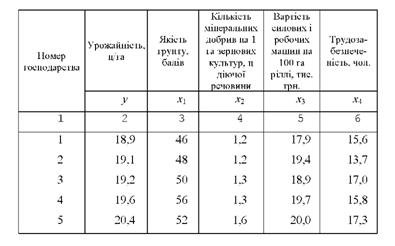
Порядок визначення і аналізу показників зв'язку при множинній кореляції розглянемо на прикладі залежності урожайності зернових культур (у) від чотирьох факторів: якості Грунту кількості мінеральних добрив, внесених на 1 га зернових культур, ц діючої речовини (*2); вартості силових і робочих машин на 100 га ріллі, тис. грн. (*3); трудозабезпеченості (кількість середньорічних працівників на 100 га сільськогосподарських угідь, чол.; (*4).

Вихідні дані подамо у вигляді матриці (табл. 9.3).

Попереднє вивчення форми залежності між вказаними ознаками показало, що зв'язок може бути виражений за допомогою лінійного рівняння регресії:

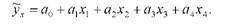
Таблиця 9.3. Матриця вихідних даних для багатофакторного кореляційно-регресійного аналізу урожайності зернових культур

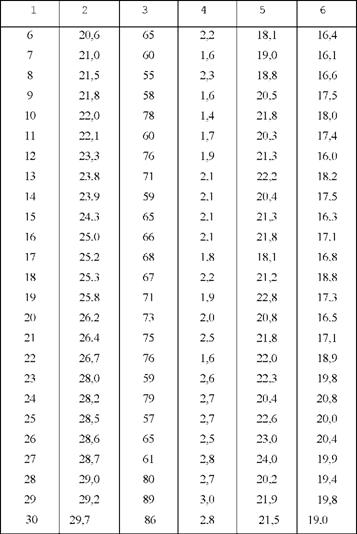
Розв'язавши рівняння множинної регресії і розрахувавши інші показники кореляційного зв'язку на ЕОМ, одержимо таку машинограму:

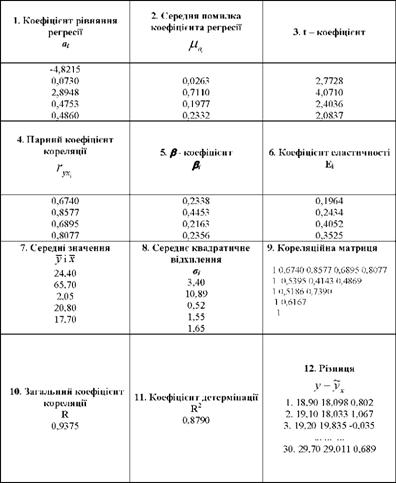
На ЕОМ одержана така кореляційна залежність урожайності від включених до моделі факторів (1-й стовпець машинограми):

ух = -4,8215 + 0,0730х,. + 2,8948х2 + 0,4753х3 + 0,4860х4.

Подальший аналіз пов'язаний з перевіркою значущості коефіцієнтів регресії. Для цього визначимо табличне значення X - критерію нормального розподілу (п > 30) і порівняємо його з фактичними значеннями (3-й стовпець машинограми).

Табличне значення і - критерію нормального розподілу при заданому рівні довірчої імовірності Р = 0,95 становитиме і = 1,96 (дод. 2).

Відповідні фактичні значення нормованих відхилень для коефіцієнтів регресії такі:

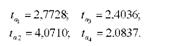
Фактичні значення коефіцієнтів і вище табличного значення (і = 1,96). Тому наведене вище рівняння регресії можна використати для подальшого аналізу.

Коефіцієнти регресії показують на скільки зміниться урожайність зернових культур при зміні кожного фактора на одиницю його виміру при фіксованих значеннях інших факторів, включених до рівняння. Так, поліпшення якості Грунту на один бал збільшує урожайність на 0,0730 ц/га. збільшення дози внесення добрив на 1 ц діючої речовини - на 2,8948 ц/га. збільшення вартості силових і робочих машин на 100 га ріллі на одну тисячу гривень - на 0,4753 ц/га, збільшення трудозабезпеченості працівниками на 100 га сільськогосподарських угідь на одного чоловіка - на 0,4860 ц/га.

Коефіцієнт множинної кореляції (10-й стовпець машинограми), який характеризує тісноту зв'язку між урожайністю та її факторами, дорівнює К = 0,9375.

Коефіцієнт множинної детермінації (11-й стовпець машинограми) К2 = 0,93752 = 0,8790 показує, що варіація урожайності в зв'язку із зміною розглядуваних факторів, становить 87,90%.

Тісноту зв'язку між ознаками, включеними в рівняння регресії характеризують 4-й 1 9-й стовпці машинограми і складена на їх основі така матриця парних коефіцієнтів кореляції:

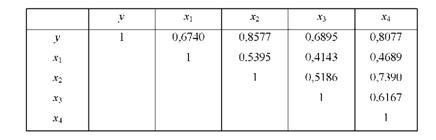
З даних матриці видно, що урожайність знаходиться в досить тісному зв'язку з включеними до моделі факторами. Так, тіснота зв'язку між урожайністю і якістю Грунту становить гУх1 = 0,6740, між дозами добрив

Гухг = 0,8577, між забезпеченістю технікою і робочою силою - відповідно

Гух3 = 0,6895 і Гух4 = 0,8077. Значна тіснота зв'язку спостерігається і між факторами.

Найбільший вплив на урожайність зернових культур, якщо робити висновки за наведеним рівнянням регресії, мають дози внесених добрив і трудозабезпеченність, тому що коефіцієнти регресії при цих коефіцієнтах найбільші (а2 = 2,8948, а4 = 0,4880), потім забезпеченість технікою (а3 = 0,4753) і якість Грунту (а1 = 0,0730).

Однак, коефіцієнти регресії, що мають різний фізичний смисл і одиниці вимірювання, не дають чіткого уявлення про те, які фактори найістотніше впливають на урожайність. Для проведення такого аналізу на ЕОМ розраховані коефіцієнти еластичності, які показують на скільки процентів зміниться величина результативної ознаки у разі зміни величини фактора на 1% при фіксованому значенні інших факторів (6-й стовпець машинограми).

На підставі обчислених коефіцієнтів еластичності

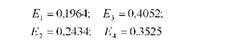
можна зробити висновок, що збільшення на 1% забезпеченості технікою веде до збільшення урожайності відповідно на 0,4052 %, трудозабезпеченості - на 0,3525 %, добрив - на 0,2434 і якості Грунту - на 0,1964 %.

Таким чином, найбільший вплив на урожайність мають забезпеченість технікою і робочою силою.

Проте і цих даних недостатньо, щоб скласти об'єктивне уявлення проте, як по групі досліджуваних господарств розподіляються фактори за їх впливом на резерви зростання урожайності зернових культур.

З цією метою на ЕОМ обчислюють /В - коефіцієнти, які показують, на скільки середньоквадратичних відхилень ау зміниться результативна ознака (урожайність) при зміні відповідного фактора на одне значення свого середньоквадратичного відхилення ау. По суті /В - коефіцієнти характеризують фактори, в розвитку яких приховано найбільші резерви збільшення результативної ознаки (урожайності).

Фактичні значення Д коефіцієнтів (5-й стовпець машинограми) такі:

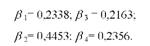
У розрахованій нами моделі найбільші можливості збільшення урожайності закладено в добривах (/¡2 = 0,4453), тому що при зміні на одне середнє квадратичне відхилення доз добрив урожайність змінюється на 0,4453 свого середнього квадратичного відхилення. Далі за ступенем впливу йдуть такі фактори: забезпеченість робочою силою (Д = 0,2356), якість Грунту (Д = 0,2338) і забезпеченість технікою (Д = 0,2163). Сила впливу на урожайність останніх трьох факторів практично є однаковою.

Коефіцієнт множинної детермінації, який дорівнює К2 = 0,8790, свідчить про те, що коливання урожайності, які пояснюються варіацією включених до рівняння регресії факторів, дорівнює 87,9 %. Викликає інтерес розкладання загального обсягу варіації урожайності на варіацію за рахунок кожного включеного в рівняння регресії фактора. Для цього розрахуємо коефіцієнти детермінації, які визначаються як добуток парних коефіцієнтів кореляції на р - коефіцієнти за відповідними факторами (4-й і 5-й стовпці машинограми).

Усі розрахунки зведемо в табл. 9.4.

Таблиця 9.4. Розкладання загального обсягу варіації за факторами

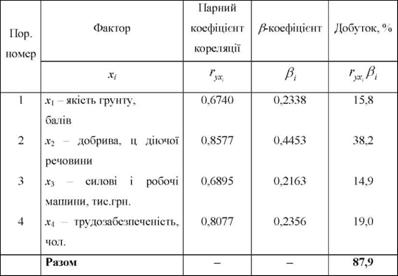
Таким чином, із 87,9% загального коливання урожайності зернових культур 15,8 % пояснюється варіацією якості Грунту, 38,2 % - кількістю внесених добрив, 14,9% - забезпеченістю технікою і 19,0% -трудозабезпеченністю. Найвпливовішим фактором, як показали розрахунки, є добрива.

Заключним етапом багатофакторного кореляційно-регресійного аналізу є оцінка результатів роботи кожного господарства за досягнутим рівнем урожайності зернових культур. Для цього потрібно порівняти розрахунковий (теоретичний) і фактичний рівні урожайності (12-й стовпець машинограми). З метою економії місця тут наведено дані лише для перших трьох і останнього господарства.

Плюсова різниця свідчить про те, що в цих господарствах фактична урожайність виявилася вищою розрахункової, а мінусова різниця навпаки.

Порівняння фактичного і теоретичного рівнів урожайності в окремих господарствах показує, що в 14 господарствах з 30 урожайність виявилася вище розрахункової. В інших 16 господарствах вона не перевищувала теоретичного рівня. Це говорить про те, що ще в багатьох господарствах не використано достатньою мірою наявні резерви збільшення урожайності зернових культур.