При кореляційному зв'язку разом з досліджуваним фактором або кількома факторами при множинній кореляції на результативну ознаку впливають і інші фактори, які не враховуються або не можуть бути точно враховані. При цьому дія їх може бути направлена як в сторону підвищення результативної ознаки, так і в сторону її зниження. Отже, дослідження зв'язку відбувається в умовах, коли цей зв'язок більшою або меншою мірою затушовується суперечливою дією інших причин. Тому одне із завдань кореляційного аналізу полягає у визначенні тісноти зв'язку між ознаками, у визначенні сили дії досліджуваного фактора (факторів) на результативну ознаку.
Тіснота зв'язку у кореляційному аналізі характеризується за допомогою спеціального відносного показника, який отримав назву коефіцієнта кореляції.
При парній лінійній залежності тіснота зв'язку визначається за допомогою лінійного коефіцієнта кореляції

Коефіцієнт кореляції знаходиться в межах від 0 до ±1. Якщо коефіцієнт кореляції дорівнює нулю, то зв'язок відсутній, а якщо одиниці, то зв'язок функціональний. Знак при коефіцієнті кореляції вказує на напрям зв'язку ("+" - прямий, "-" - обернений). Чим ближче коефіцієнт кореляції до одиниці, тим зв'язок між ознаками тісніший.
Квадрат коефіцієнта кореляції називається коефіцієнтом детермінації (г2). Він показує, яка частка загальної варіації результативної ознаки визначається досліджуваним фактором. Якщо коефіцієнт детермінації виражений в процентах, то його слід читати так: варіація (коливання) залежної змінної на стільки-то процентів зумовлена варіацією фактора.
Між лінійним коефіцієнтом кореляції (г) і коефіцієнтом повної регресії (Ь) є такий зв'язок:
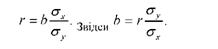
Отже, знаючи коефіцієнт кореляції (г) і значення середніх квадратичних відхилень по х і у, можна визначити коефіцієнт регресії (Ь) і навпаки, знаючи коефіцієнт регресії (Ь) і відповідні середні квадратичні відхилення можна обчислити коефіцієнт кореляції (г).
При парній лінійній залежності коефіцієнт кореляції і коефіцієнт повної регресії мають однакові знаки (плюс, мінус).
Лінійний коефіцієнт кореляції призначений для оцінки ступеня тісноти зв'язку при лінійній залежності. Для випадків нелінійного зв'язку між ознаками використовується інша формула коефіцієнта кореляції, яка випливає з правила додавання дисперсій:
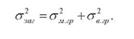
Із наведеної рівності видно, що чим більшим є вплив фактора на результативну ознаку, тим більшою мірою значення її дисперсії ("м.гр ) наближається до значення загальної дисперсії результативної ознаки.
Відповідно, чим більше "м.гР і менша ае.гр тим зв'язок між ознаками буде тіснішим і навпаки. Відтак, відношення міжгрупової (факторної) і загальної дисперсій використовується для оцінки тісноти зв'язку між ознаками. Формула коефіцієнта кореляції має вигляд:

Враховуючи, щосг2я = о-а-огля!>, формулу коефіцієнта кореляції можна подати як

Обидві формули коефіцієнта кореляції застосовуються для обчислення тісноти зв'язку при будь-якій формі зв'язку.
Із правила додавання дисперсій видно, що значення коефіцієнта кореляції перебуває в межах від 0 до 1. Знак коефіцієнта кореляції з формули не виводиться. Якщо вивчається зв'язок між двома ознаками (парна проста кореляція), то напрямок зв'язку (знак перед г) визначається безпосередньо за знаком перед коефіцієнтом регресії лінійного рівняння.
При парній криволінійній залежності, тіснота зв'язку як і при лінійній залежності, визначається за допомогою спеціального показника, аналогічного розглянутому вище коефіцієнту кореляції г.
Цей показник (щоб підкреслити його належність до криволінійного зв'язку) позначають символом іг і називають індексом кореляції:
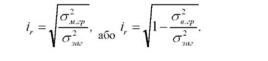
Числове значення індексу кореляції аналогічне коефіцієнту кореляції: якщо іг = 1 - зв'язок функціональний, якщо іг = 0 - зв'язок відсутній; чим іг ближче до одиниці, тим зв'язок між ознаками тісніший.
Якщо відомі коефіцієнти регресії рівняння зв'язку, то індекс кореляції можна визначити за іншою, простішою формулою. Так, при параболічній залежності формула індексу кореляції може бути подана як
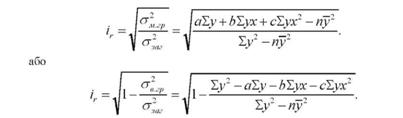
Тіснота зв'язку при множинній кореляції визначається за допомогою коефіцієнта множинної кореляції (її) і коефіцієнта множинної детермінації (її2). За змістом вони аналогічні коефіцієнтам кореляції і детермінації при парному зв'язку. їх обчислення ґрунтується на порівнянні міжгрупової (факторної) і загальної дисперсій:
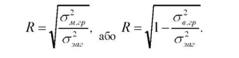
Ця формула може бути застосована для визначення тісноти зв'язку при будь-якій формі зв'язку.
Величина рч. змінюється від 0 до 1 і розглядається як додатна, оскільки при множинних залежностях зв'язок результативної ознаки з одними факторами може бути додатнім, а з іншими - від'ємним.
Для випадку залежності результативної ознаки від двох факторів формула коефіцієнта множинної кореляції має вигляд

де Гі - парні лінійні коефіцієнти кореляції.
Наведена формула застосовується для визначення тісноти зв'язку при лінійній залежності.
Для визначення тісноти зв'язку між результативною ознакою і кожним фактором при виключені впливу інших факторів визначають часткові коефіцієнти кореляції, які характеризують "чистий" вплив фактора на результативну ознаку. Для їх розрахунку використовують парні коефіцієнти кореляції.
У випадку залежності результативної ознаки від двох факторів (х1 і х2) можна розрахувати три коефіцієнта часткової кореляції:
1) між у і х1 при виключенні впливу х2:
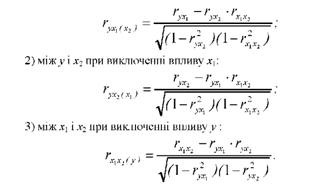
Коефіцієнти кореляції при парних і множинних зв'язках, а також індекс кореляції - це відносні величини, тому вони можуть бути використані для зіставлення тісноти зв'язку по кількох явищах, що аналізуються.
Слід мати на увазі, що показники тісноти зв'язку залежать від розмаху варіювання досліджуваних ознак. Чим більшою є варіація змінних, тим вищою буде величина показників тісноти зв'язку.
Визначимо тісноту зв'язку між досліджуваними ознаками для нашого прикладу. Оскільки між продуктивністю корів і рівнем годівлі має місце лінійний зв'язок, тісноту зв'язку визначимо за допомогою лінійного коефіцієнта кореляції

Коефіцієнт кореляції показує, що між продуктивністю корів і рівнем годівлі має місце тісний (сильний) зв'язок.
Коефіцієнт детермінації г2 = 0,93442 = 0,8731 показує, що 87,31% загального коливання продуктивності корів зумовлено відмінностями у рівні годівлі, а решта 12,69% (100 - 87,31) - іншими факторами, які в даному випадку не було враховано.
Коефіцієнт кореляції можна знайти і за іншими формулами:
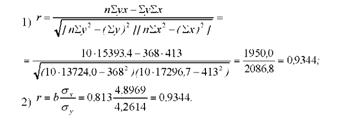
9.5. Статистична оцінка вибіркових показників зв'язку
9.6. Непараметричні критерії оцінки кореляційного зв'язку
9.7. Особливості кореляційного аналізу в рядах динаміки
Розділ 10. Ряди динаміки
10.1. Поняття про ряди динаміки і їх види. Наукові умови побудови рядів динаміки
10.2. Показники ряду динаміки
10.3. Прийоми виявлення основної тенденції розвитку в рядах динаміки
10.4. Факторний аналіз рядів динаміки
10.5. Інтерполяція і екстраполяція. Прогнозування суспільних явищ