Теорія статистики - Мармоза А.Т. - 10.3. Прийоми виявлення основної тенденції розвитку в рядах динаміки

Для всебічної характеристики зміни соціально-економічних явищ у часі розрахунку тільки одних показників динаміки та їхніх середніх величин не досить. В зв'язку з цим статистика пропонує ряд спеціальних прийомів обробки й аналізу динамічних рядів.

Важливе місце у вивченні розвитку суспільних явиш належить порівняльному аналізу кількох рядів динаміки. При цьому можна порівнювати динамічні ряди як однойменних, так і різнойменних показників, що стосуються різних територій або є складовими частинами цілого. Абсолютні рівні таких рядів динаміки, як правило, внаслідок відмінностей методики обчислення показників, грошової оцінки продукції та інших причин безпосередньо непорівнянні. Тому доцільно порівнювати не абсолютні, а відносні показники і за ними робити висновки про те, яке явище і на якій території зростає (або знижується) швидше. Цей прийом дістав назву приведення рядів динаміки до однієї основи, тобто до загальної бази порівняння, яку беруть за одиницю або за сто процентів.

Суть цього прийому полягає в тому, що дані про величину показника, що вивчається, за рік (або інший відрізок часу), взятий за базу порівняння, беруть таким, що дорівнює 100%, а рівні окремих років (або інших відрізків часу) порівнюють з ним, а частку виражають в процентах.

Практичне застосування прийому приведення рядів динаміки до однієї основи розглядається в наступному параграфі розділу підручника, присвяченому факторному аналізу рядів динаміки (табл. 10.13 і 10.14).

У тих випадках, коли рівні ряду динаміки за одні роки непорівнянні з рівнями за інші роки в зв'язку з територіальними, відомчими, організаційними змінами, зміною методики обчислення показників або за іншими причинами і виникає потреба забезпечити порівнянність рівнів, удаються до змикання динамічних рядів, тобто об'єднання двох і більше рядів в один зімкнутий ряд.

Суть цього прийому полягає в наступному. Рівні року, протягом якого відбулися зміни, як до змін, так і після змін, беруть за базу порівняння (звичайно за 100%), інші - порівнюються з ним і виражають у процентах. В результаті цього дістанемо єдиний ряд відносних величин, що характеризує зміну досліджуваного явища за весь період.

Припустимо, є дані за 2004 - 2010 рр. щодо посівної площі картоплі в господарствах району, в територіальних межах якого в 2007 р. відбулися зміни (табл. 10.5).

Аналіз таблиці показує, що в зв'язку із зміною меж району в 2007 р. дані про посівну площу картоплі за 2008 - 2010 рр. непорівнянні з даними за 2004 - 2006 рр. Щоб мати порівнянні дані, виконаємо змикання цих рядів динаміки.

Таблиця 10.5. Динаміка посівної площі картоплі в господарствах району за 2004 - 2010 рр., га

Змикання рядів динаміки і зведення їх до порівнянного вигляду здійснимо двома способами:

а) вираженням ряду динаміки у відносних показниках, прийнявши за базу порівняння один і той самий період;

б) перерахунком абсолютних показників.

Змикання рядів способом вираження рядів відносними показниками динаміки виконаємо так. Візьмемо рік, в якому відбулися територіальні зміни (в нашому прикладі це 2007 р.) за базу порівняння або 100%, а решту рівнів порівняємо з цим роком і отримані дані виразимо в процентах. Отже, за 100% для першого ряду динаміки (2004 - 2007 рр.) буде прийнята величина посівної площі картоплі, що дорівнює 2430 га, а для другого ряду динаміки (2007 -2010 рр.) - 2686 га.

Так, наприклад, відносний показник динаміки посівної площі в 2001 р. порівняно з 2007 р. становитиме 86,4% [(2100 :2430>100], в 2010 р. порівняно з 2007 р, - 106,5% [(2861 : 2686) -100] і т.д.

Внаслідок отримаємо ряди відносних показників динаміки посівної площі картоплі з однаковою базою порівняння, які можна замінити одним зімкнутим рядом.

Змикання рядів динаміки способом перерахунку абсолютних показників здійснено за допомогою коефіцієнта перерахунку (Кп), який визначимо як відношення двох рівнів посівної площі після зміни меж району до посівної площі перед цією зміною:

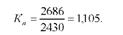
Перемноживши посівну площу картоплі першого ряду динаміки (2004 -2006рр.) на коефіцієнт перерахунку, матимемо дані, які порівняні з даними про посівну площу картоплі другого ряду динаміки ( 2008 - 2010рр.). Так, у 2004р. посівна площа картоплі в порівняному показникові дорівнюватиме 2320 га (2100-1,105), в 2005 р. - 2440 га (2208-1,105) і т.д.

Усі розрахунки з приведення рядів динаміки до порівнянного вигляду зведемо в табл. 10.6.

Таблиця 10.6. Зімкнуті ряди відносних і абсолютних змін посівної площі картоплі в господарствах району за 2001 - 2010 рр.

Добуті зімкнуті ряди динаміки дають змогу зробити дані про посівну площу картоплі за різні роки порівнянними, з них видно, що посівна площа картоплі в районі як в абсолютних, так і у відносних показниках систематично зростала.

Під впливом випадкових факторів (у сільськогосподарському виробництві до них відносять передусім метеорологічні умови) рівні ряду динаміки часто-густо сильно коливаються по періодах часу, при цьому тенденція розвитку затушовується, наочно не проявляється. В зв'язку з цим одним із основних завдань аналізу рядів динаміки є виявлення основної тенденції розвитку соціально-економічних явищ. Під загальною тенденцією динамічного ряду розуміють тенденцію до зростання, зниження або стабілізації рівня будь-якого суспільного явища.

Виявлення тенденції в динамічних рядах дає змогу оцінити характер розвитку досліджуваного явища, визначити ефективність факторів, що формують основну тенденцію, встановити рівні досліджуваного явища на перспективу.

Виявлення основної тенденції зміни рівнів динамічного ряду передбачає її кількісне вираження, в деякій мірі вільної від випадкових причин. Це досягається шляхом абстрагування від індивідуальних, випадкових змін ознаки. Виявлення основної тенденції розвитку (тренда) називається у статистиці також вирівнюванням часового ряду, а прийоми виявлення основної тенденції - прийомами вирівнювання. Вирівнювання дає змогу охарактеризувати особливості зміни у часі даного динамічного ряду в найбільш загальному вигляді як функцію часу, передбачаючи, що через час можна виразити вплив основних факторів.

У практиці економічного аналізу нерідкі випадки, коли загальна тенденція явища до зростання або зниження проявляється досить чітко. Наведені дані про динаміку поголів'я корів (табл. 10.3) показують, що в динамічному ряду має місце загальна тенденція до зростання поголів'я корів. Проте для виявлення тенденції в рядах динаміки не досить одного візуального аналізу ряда, якщо його рівні через будь-які об'єктивні або випадкові причини істотно коливаються, то зростаючи, то знижуючись. Це затушовує, наочно не проявляє основну тенденцію розвитку явища. Наприклад, якщо урожайність будь-якої сільськогосподарської культури під впливом метеорологічних умов, що діють в різних напрямках, дуже коливається по роках, то основна тенденція зміни урожайності може не проявлятися безпосередньо. В таких випадках для проявлення основної тенденції потрібно вдатися до спеціальних прийомів обробки динамічних рядів.

До таких прийомів відносяться укрупнення періодів, згладжування ряду динаміки способом ковзної середньої, вирівнювання ряду динаміки по середньому абсолютному приросту, середньому коефіцієнту зростання і способу найменших квадратів (аналітичне вирівнювання рядів динаміки).

Розглянемо на конкретних прикладах умови і техніку виявлення основної тенденції розвитку динамічних рядів кожним із названих прийомів.

Одним з найпростіших прийомів виявлення тенденції розвитку є прийом укрупнення періодів. Суть його полягає в тому, що абсолютні або середні рівні ряду динаміки за короткі інтервали (рік, місяць, декаду, день тощо), що зазнають випадкових коливань, замінюють узагальнюючим (звичайно середнім) значенням за триваліший період (триріччя, п'ятиріччя тощо).

По суті спосіб укрупнення періодів являє собою типологічне групування рівнів ряду динаміки, тому при його застосуванні необхідно дотримуватись наукових основ побудови статистичних групувань.

При укрупненні періодів дуже важливо науково обґрунтовано і правильно виділити періоди часу для укрупнення. Періоди, що їх виділяють, мають бути однорідними в якісному відношенні і досить тривалими за часом, щоб відбулося погашення випадкових коливань явища.

Застосування цього прийому, як правило, пов'язується з використанням рівних за тривалістю періодів. Проте тривалість періодів може бути різною. Виділення нерівних періодів зумовлюється наявністю якісних специфічних періодів в розвитку того або іншого соціально-економічного явища.

Покажемо порядок розрахунку укрупнених періодів, використовуючи дані про урожайність соняшнику за 15 років (табл. 10.7).

Таблиця 10.7. Динаміка урожайності соняшнику в ТОВ району за 1996 - 2010 рр.

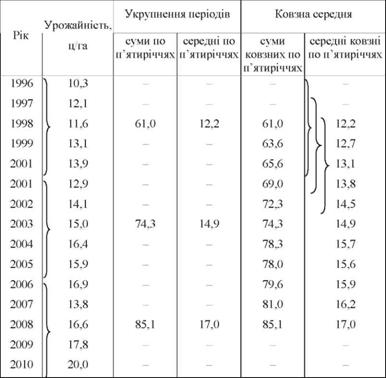
Обґрунтуємо тривалість укрупнених періодів для нашого прикладу. Аналіз вихідного ряду динаміки показує, що яких-небудь якісних періодів або періодичних коливань всередині динамічного ряду урожайності за досліджуваний період не спостерігається.

Як показує аналіз вихідного ряду динаміки, урожайність в господарствах району змінюється поступово, тенденція її зміни затушовується в окремі роки головним чином метеорологічними умовами. Оскільки вплив метеорологічних умов для досліджуваної зони в більшості випадків вирівнюється по п'ятирічних періодах, укрупнення здійснено по п'ятиріччях. Завдяки такому укрупненню взаємопогасяться випадкові фактори і виявиться загальна тенденція зміни урожайності.

Щоб отримати середні рівні по п'ятиріччях, спочатку знайдемо суми урожайності за кожне п'ятиріччя (1996 - 2000 рр., 2001 - 2005рр., 2006 - 2010 рр.), а потім добуті суми поділимо на кількість років в укрупненому періоді (п'ять).

Знайдені суми і середні запишемо центруючи їх на середину кожного п'ятиріччя (відповідно 1998 р., 2003 р. і 2008 р.).

В результаті проведеного укрупнення періодів ряду динаміки чіткіше проявляється тенденція зростання урожайності за роки, що аналізуються. Так, добуті результати показують, що від п'ятиріччя до п'ятиріччя урожайність соняшнику в TOB району систематично зростала (з 12,2 ц/га в 1996 - 2000 рр. до 17,0 ц/га в 2006 - 2010 рр., тобто на 4,8 ц/га, або на 39,3%).

При укрупненні періодів число членів динамічного ряду дуже скорочується. Цей істотний недолік значною мірою усувається при використанні прийому вирівнювання динамічних рядів способом ковзних середніх.

Цей спосіб також ґрунтується на укрупненні періодів. Суть розрахунку ковзних середніх полягає в тому, що склад періоду безперервно і постійно змінюється - відбувається зсув на одну дату при збереженні постійного інтервалу періоду (триріччя, п'ятиріччя тощо).

Ковзна середня - це середня укрупнених періодів, створених послідовним виключенням кожного початкового рівня інтервалу і заміни його черговим наступним рівнем ряду. Таким чином, відбувається ніби ковзання періоду і отриманої середньої по динамічному ряду. Наприклад, при згладжувані по триріччях

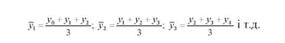
Цей прийом, як і попередній, ґрунтується на відомому теоретичному положенні про те, що в середніх величинах взаємно погашаються випадкові відхилення і виявляється типове, закономірне.

При виявленні тенденції прийомом ковзних середніх, так само як і при використанні прийому укрупнення періодів, одним з важливих питань є питання щодо тривалості періодів. Інтервал має бути досить великим і забезпечити взаємне погашення випадкових відхилень рівнів. Якщо в розвитку явища має місце циклічність (періодичність), то інтервал ковзання слід брати рівним тривалості циклу. Чим довше інтервал ковзання, тим більшою мірою вирівнюється ряд в результаті усереднення вихідних рівнів.

Покажемо порядок розрахунку ковзних середніх, використовуючи дані про урожайність соняшнику (табл. 10.7).

Ковзні середні розрахуємо також по п'ятирічних періодах. Для розрахунку ковзних середніх підсумуємо урожайність за перші п'ять років (1996 - 2000 рр.). а потім, опускаючи дані першого в ряду динаміки року, підсумуємо урожайність за наступне п'ятиріччя (1997 - 2001 рр.) і т.д. Відбувається як би ковзання по ряду динаміки. Добуті суми поділимо на число років в періоді ковзання (п'ять), а обчислену середню віднесемо до середини періоду ковзання (в нашому прикладі третій рік кожного п'ятирічного періоду ковзання).

Розраховані ковзні середні показують стійку тенденцію зростання урожайності соняшнику в TOB району.

Ковзна середня згладжує варіацію рівнів, але не дає ряду динаміки, в якому всі вихідні рівні були б замінені вирівняними. Це пояснюється недоліком вирівнювання ряду способом ковзної середньої, при якому вирівняний ряд "скорочується" порівняно з вихідним на (n - rm):2 члена з одного та другого кінця (під п розуміють число членів, з яких визначають ковзні середні).

Прагнення в процесі вирівнювання ряду замінити всі вихідні рівні вирівняними зумовлює застосування досконаліших прийомів вирівнювання рядів динаміки. До таких прийомів належать: вирівнювання по середньому абсолютному приросту, середньому коефіцієнту зростання і способу найменших квадратів.

В основі застосування способу вирівнювання ряду динаміки по середньому абсолютному приросту лежить припущення, що кожен наступний рівень змінюється порівняно з попереднім приблизно на однакову величину, що дорівнює середньому абсолютному приросту.

Рівняння, що відображає тенденцію розвитку явища за цим способом вирівнювання ряду динаміки, має вигляд:

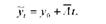
де у - вирівняні рівні ряду динаміки;

у0 - початковий рівень ряду динаміки;

А - середній абсолютний приріст;

і - порядковий номер дати (і = 1,2,3,...,п).

Техніку виявлення тенденції на основі середнього абсолютного приросту розглянемо на прикладі динамічного ряду посівної площі цукрових буряків (табл. 10.8).

Аналіз ряду динаміки показує, що для нього характерне постійне збільшення посівної площі цукрових буряків. При цьому щорічні абсолютні прирости посівної площі стабільні і становлять близько 10 га. Найбільш прийнятнішим способом вирівнювання рядів динаміки, які мають сталі абсолютні прирости, є спосіб вирівнювання рядів по середньому абсолютному приросту.

Таблиця 10.8. Динаміка посівної площі цукрових буряків в господарстві за 2005 - 2010 рр.

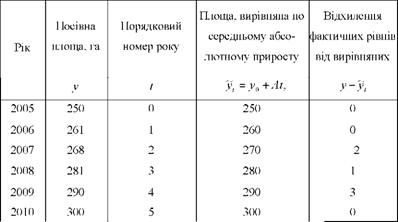
Визначимо середній абсолютний приріст посівної площі:

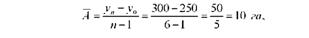
де у0 - початковий рівень ряду динаміки ;

уп - кінцевий рівень ряду динаміки ;

п - число рівнів ряду динаміки (п = 6 років).

Отже, посівна площа цукрових буряків щорічно збільшувалась в середньому на 10 га.

Визначимо вирівняні по середньому абсолютному приросту значення посівної площі для кожного року, підставляючи у рівняння замість і його значення:

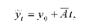
де і - порядковий номер року (і = 0,1,2,3,4,5). Вирівняні значення посівної площі становитимуть:

в 2005 р. (при і = 0) у = у0 + Лі, = 250 + 10-0 = 250 га;

в 2006 p. (при t = 1~t = y0 + At,= 250 + 10-1 = 260 rai т.д. Вирівняний по середньому абсолютному приросту ряд динаміки на графіку являє собою пряму лінію, яка з'єднує мінімальне і максимальне значення. Як видно з таблиці, відхилення фактичних рівнів від вирівняних незначні. Отже, вирівнювання ряду динаміки по середньому абсолютному приросту дало змогу точніше відобразити тенденцію зміни посівної площі цукрових буряків в господарстві.

Водночас необхідно відмітити, що теоретична лінія, яка вирівнює ряд динаміки, цілком залежить тільки від двох крайніх значень рівнів ряду динаміки (початкового і кінцевого), які можуть суттєво змінюватись під впливом випадкових коливань. Відповідно тенденція, яка дійсно має місце в досліджуваному явищі, буде спотворена. В зв'язку з цим прийом вирівнювання рядів динаміки по середньому абсолютному приросту доцільно використовувати лише для рядів, що мають стабільні щорічні абсолютні прирости. Практично цей прийом використовується в динамічних рядах, які охоплюють нетривалий період часу, протягом якого не відбувається суттєвих якісних змін у рівнях факторів, що визначають тенденцію, і ступеня їх впливу на досліджувану ознаку.

Вирівнювання ряду динаміки по середньому коефіцієнту зростання застосовується в тих випадках, коли в досліджуваному ряду кожен наступний рівень змінюється порівняно з попереднім приблизно в одну і ту саму кількість разів, що дорівнює величині середнього коефіцієнта зростання, тобто коли фактори, що визначають основну тенденцію, зумовлюють від періоду до періоду однакові коефіцієнти зростання досліджуваного явища.

Вирівняні значення рівнів ряду динаміки визначають за формулою:

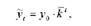
де к - середній коефіцієнт зростання.

Порядок вирівнювання по середньому коефіцієнту зростання розглянемо на прикладі динаміки фондозабезпеченості (табл. 10.9).

Таблиця 10.9. Динаміка вартості основних виробничих фондів тваринництва в ТОВ за 2005 - 2010 рр.

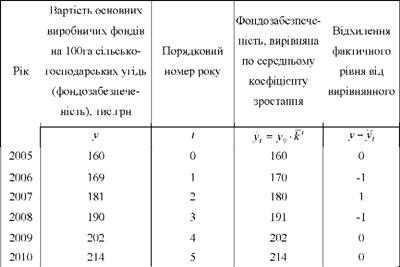
Аналіз динамічного ряду показує, що абсолютні прирости збільшуються від 9 - 10 тис. грн. у перші роки до 12 тис. грн. в останні роки, а коефіцієнти зростання залишаються приблизно однаковими і становлять 1,06 - 1,07. Отже, для даного динамічного ряду характерно збільшення кожного наступного рівня порівняно з попереднім в ту саму кількість разів, яка дорівнює величині середнього коефіцієнта зростання. Тому даний ряд динаміки доцільно вирівнювати по середньому коефіцієнту зростання.

Визначимо середній коефіцієнт зростання фондозабезпеченості за формулою:

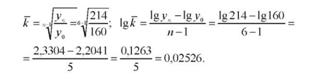
За таблицями антилогарифмів встановимо значення к = 1,06.

Отже, фондозабезпеченість господарства щороку в середньому зростала в 1,06 раза, або на 6,0%.

Обчислимо вирівняні по середньому коефіцієнту зростання значення фондозабезпеченості:

в 2005 р. (при X = 0) у = у0 ■ к' = 160-1,06° = 160 тис. грн;

в 2006 р. (при X = 1) у, = у0 ■ к' = 160-1,061 = 170 тис. грн і т.д.

Слід мати на увазі, що при визначенні вирівняних значень рівнів ряду динаміки по середньому коефіцієнту зростання, так само як і при вирівнюванні по середньому абсолютному приросту, у вихідному і вирівняному рядах динаміки початкові і кінцеві рівні збігаються.

Вирівняний по середньому коефіцієнту зростання ряд динаміки являє собою показникову криву. Цьому способу вирівнювання рядів динаміки притаманний той самий недолік, що й вирівнюванню по середньому абсолютному приросту. Тут при визначенні вирівняних значень використовуються тільки два крайніх рівні динамічного ряду (початковий і кінцевий), які внаслідок впливу випадкових факторів можуть бути нехарактерними для досліджуваного суспільного явища.

Досконалішим і точнішим прийомом вирівнювання рядів динаміки, який враховує всі рівні вихідного ряду, є аналітичне вирівнювання по способу найменших квадратів.

Вирівнювання по цьому способу ґрунтується на припущенні, що зміни досліджуваного ряду динаміки можуть бути наближено виражені певним математичним рівнянням (апроксимуючою функцією), за яким і визначають вирівняні рівні динамічного ряду. Іншими словами, рівні ряду динаміки розглядаються як функція часу у1 = /(') , де у1 - рівні динамічного ряду, визначені за відповідним рівнянням на момент часу '.

Аналітичне вирівнювання можна провести з використанням різних типів функцій: прямої лінії, параболи другого порядку, показникової кривої (експоненти), гіперболи тощо.

Рівняння, що виражає рівні ряду динаміки як деяку функцію часу t, називають трендом. Поняття про рівняння тенденції було введене в статистику англійським вченим Гукером у 1902 р. Він запропонував називати таке рівняння трендом (the trend).

Суть аналітичного вирівнювання динамічних рядів полягає в тому, що фактичні рівні ряду замінюються рядом рівнів, які змінюються плавно (теоретичними рівнями), обчисленими на основі певної кривої, вибраної в припущенні, що вона найточніше відображає загальну тенденцію зміни досліджуваного соціально-економічного явища у часі.

Підбір найбільш придатної функції є важливим і відповідальним завданням, від якого в остаточному підсумку залежать результати вирівнювання. В основі вирішення його має бути змістовний теоретичний аналіз істотності досліджуваного явища і законів його розвитку. Треба підібрати таку криву, яка б максимально близько проходила до фактичних рівнів. Добитися цього можна за умови, що сума квадратів відхилень фактичних рівнів (у ) від розрахованих за рівнянням (~(), буде мінімальною У(у -~()2 = min.

У практиці економічних досліджень найчастіше застосовують такий підхід: добирають кілька рівнянь, визначають їх параметри, а потім віддають перевагу тому, в якого У/у ~Л )2 і коефіцієнт варіації найменші.

Наближено обґрунтувати рівняння, що відображує основну тенденцію, можна за допомогою побудови графіка (лінійної діаграми).

Вирівнювання динамічних рядів способом найменших квадратів, як і вирівнювання за допомогою інших прийомів, має здійснюватись в межах одноякісних періодів. Якщо в динамічному ряду є якісно специфічні періоди, то виявляти тенденцію доцільно в межах кожного з них.

Залежно від вихідних даних для вирівнювання рядів динаміки можуть бути вибрані різні типи кривих або пряма лінія. Аналіз динаміки соціально-економічних явищ показує, що їхня зміна супроводжується постійними зростаючими і спадаючими абсолютними приростами, постійними темпами зростання і приросту, прискоренням або уповільненням, тобто їхнє вирівнювання слід здійснювати за рівнянням прямої лінії, парболи другого порядку або показникової кривої.

Основна тенденція (тренд) показує, як впливають систематичні фактори на рівні ряду динаміки, а відхилення фактичних рівнів від вирівняних характеризує варіацію рівнів, викликану індивідуальними особливостями кожного періоду. Випадкова (залишкова) варіація в рядах динаміки може бути виміряна способами, якими вимірюється звичайна варіація, наприклад за допомогою залишкового середнього квадратичного відхилення

або коефіцієнта варіації V = -100%.

Показники варіації рівнів динамічних рядів можуть бути використані для оцінки правильності вибору апроксимуючої функції (рівняння) для вирівнювання, а також оцінки порівняльної стійкості окремих динамічних рядів. Очевидно, що чим показники варіації менше, тим вирівнювання здійснене точніше, а ряди динаміки стійкіші.

Вирівнювання динамічних рядів за рівнянням прямої лінії доцільно проводити тоді, коли для емпіричного ряду характерні більш або менш постійні ланцюгові абсолютні прирости, тобто тоді, коли рівні ряду змінюються приблизно в арифметичній прогресії.

Стосовно рядів динаміки аналітичне рівняння прямої лінії має вигляд:

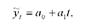
де уг - вирівняні значення рівнів динамічного ряду;

г - час, тобто порядкові номери періодів;

а0 і а1 - параметри рівняння шуканої прямої;

а0 - початок відліку (економічного змісту не має);

а1 - коефіцієнт регресії або пропорційності, який показує середній щорічний приріст (зниження) досліджуваного явища (тангенс кута нахилу прямої лінії до осі абсцис).

Параметри а0 і а1 шуканої прямої, що задовольняють вимозі способу найменших квадратів, знаходять розв'язуючи таку систему нормальних рівнянь:

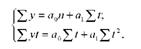
де п - число рівнів ряду динаміки.

Техніка утворення системи рівнянь така. Перше рівняння дістають множенням всіх членів вихідного рівняння (~г = а0 + а1г) на коефіцієнт при а0 (на одиницю) і підсумовування знайдених добутків. Щоб мати друге рівняння, всі члени вихідного рівняння необхідно помножити на коефіцієнт при а1 (на г) і знайдені добутки підсумувати. Аналогічно будують систему нормальних рівнянь і для інших кривих (параболи другого порядку, гіперболи тощо).

Розрахунок параметрів рівняння (а0 і а1 ) можна значно спростити, якщо відлік часу (г) проводити так, щоб сума показників часу дорівнювала нулю (X г = 0). Цього досягають так. Рівень, що знаходиться в середині ряду динаміки, беруть за умовний початок відліку, або нульове значення. Для того, щоб сума показників часу дорівнювала нулю, умовні позначення дат потрібно давати так.

При непарному числі рівнів ряду динаміки для отримання Xг = 0 рівень, що знаходиться в середині ряду, прирівнюють до нуля, а рівні, розташовані вище його позначають числами із знаком мінус -1, -2, -3 і т.д., а нижче - числами із знаком плюс +1, +2, +3 і т. д.

При парному числі рівнів ряду динаміки рівні, що лежать вище серединного значення (воно знаходиться в середині між двома серединними датами), позначають натуральними числами із знаком мінус - 1, - 3, - 5 і т.д., а рівні, що лежать нижче серединного значення - натуральними числами із знаком плюс +1, +3, +5 і т.д.

За умовою, що Xі = 0, система нормальних рівнянь спрощується і

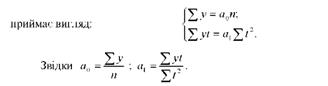
Розв'язуючи вихідну систему нормальних рівнянь способом визначників, параметри а0 і а1 можна обчислити за іншими формулами, які дають змогу дістати точніші результати за рахунок зведення до мінімуму помилки через закруглення в обчисленнях параметрів:

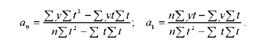
Отже, для визначення параметрів а0 і а1 необхідно мати чотири суми: Іу; Іуі; " і/

Якщо ж Хі = 0, то тоді формули для обчислення параметрів а0 і а1, спрощуються, набираючи такого вигляду:

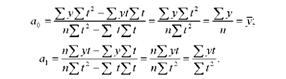
Значення X і можна обчислити за формулою:

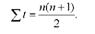
За умов, що X г = 0, значення X г2 можна відшукати за формулами:

. . " 2 (п - 1)п(п +1) п(п -1) при парному числі рівнів ^ г =---- = --

. . " 2 (п - 1)п(п +1) п(п -1) при непарному числі рівнів ^ г =-12-= -12-;

Для обчислення параметрів а0 і а1 можна користуватися формулами:

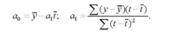
Порядок вирівнювання за рівнянням прямої лінії проілюструємо на прикладі ряду динаміки урожайності соняшнику (табл. 10.10).

Обґрунтуємо вибір математичного рівняння для вирівнювання динамічного ряду. З даних таблиці видно, що зростання урожайності відбувається рівномірно. Побудова лінійної діаграми (див. рис. 10.1) показує, що ламана крива за своєю формою близька до прямої лінії. Виходячи з цього, доцільніше цей ряд динаміки вирівнювати за рівнянням прямої лінії (лінійному тренду):

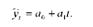
Параметри а0 і а1 шуканої прямої, яка задовольняє способу найменших квадратів, знайдемо розв'язавши таку систему нормальних рівнянь:

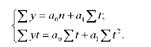
Отже, щоб визначити параметри рівняння, необхідно знайти такі чотири суми:Ху; Іуг; Іг; Xг2.

Усі розрахунки зведемо в табл. 10.10.

Вирівнювання динамічного ряду проведемо двома способами - звичайним і спрощеним (способом відліку від умовного початку),

І спосіб.

Використовуючи отримані величини, розв'яжемо систему рівнянь:

Таблиця 10.10. Розрахункові дані для аналітичного вирівнювання динамічного ряду урожайності соняшнику способом найменших квадратів

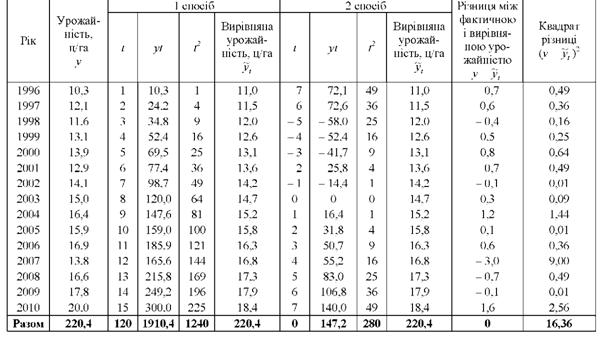
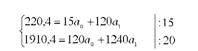
Поділимо обидва рівняння на коефіцієнти при а0: перше рівняння на 15, а друге - на 120, а потім віднімемо від другого рівняння перше:

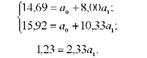
Звідси а1 = 0,5279 = 0,53 ц/га.

Визначимо а0, підставивши в одно з рівнянь значення а1:

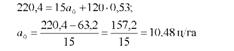
Параметри рівняння можна визначити і за іншими, зручнішими, формулами:

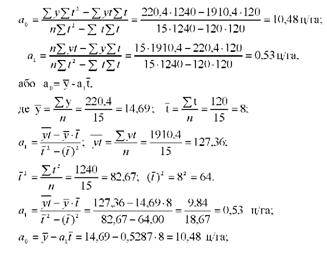
Перевіримо правильність розв'язання системи рівнянь, виходячи з рівності:

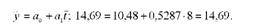
Таким чином, рівняння прямої лінії, що вирівнює ряд динаміки, має вигляд:

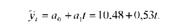
Коефіцієнт регресії а1 = 0,53 ц/га показує, що в середньому за досліджуваний період урожайність соняшнику щорічно підвищувалася на 0,53 ц/га. Коефіцієнт а0 = 10,48 ц/га - значення вирівняної урожайності для року в динамічному ряду, взятого за початок відліку (2003 р., коли г = 0).

Підставляючи в отримане рівняння значення (і = 1, 2,..., 15), дістанемо вирівняні (розрахункові) значення урожайності. Наприклад.

для 1998р. ~г=1 = 10,48 + 0,53 -1 = 11,0 ц/га;

для 1997р. ~г=2 = 10,48 + 0,53 o 2 = 11,5 ц/га і т.д.

Перевіримо правильність всіх розрахунків, порівнюючи суми фактичної і вирівняної урожайності:

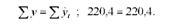
II спосіб.

Для спрощення розрахунків використаємо спосіб відліку від умовного початку. Виразимо значення дат (г) у відхиленнях від дати, взятої за умовний початок (вона знаходиться в центрі ряду динаміки; г = 0 в 2003р.; табл., 10.10). Система рівнянь спрощується, оскільки Xг = 0:

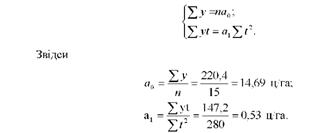
Параметри рівняння можна знайти і за іншими, наведеними у першому способі, формулами розв'язання прикладу. їхні значення будуть такими самими.

Рівняння лінійного тренду має вигляд:

у, = а0 + а1і = 14,69 + 0,53і.

Параметр а0 = 14,69 ц/га - значення вирівняної урожайності для центрального в динамічному ряду року, взятого за початок відліку. Для 2000 р. і = 0, тоді у1 = 14,69 + 0,53-0 = 14,69 ц/га. Параметр а0 дорівнює середній урожайності в динамічному ряду у = £ у: п = 220,4:15 = 14,69 ц/га. Коефіцієнт регресії а1 = 0,53 ц/га характеризує середнє щорічне збільшення урожайності. Він має таке саме значення і зміст, що й при вирівнюванні першим способом.

Вирівняні (теоретичні) рівні урожайності (у) обчислюють аналогічно тому, як це було зроблено в першому способі розрахунків.

Щоб оцінити ступінь наближення лінійного тренду до фактичних даних динамічного ряду, розрахуємо залишкове середнє квадратичне відхилення і коефіцієнт варіації. Для цього обчислимо відхилення фактичної урожайності від вирівняної (у - уі), їх квадрати (у - у )2 і їх суму £ (у - у1 )2 (гр.11 і 12 табл. 10.10).

Залишкове середнє квадратичне відхилення становитиме:

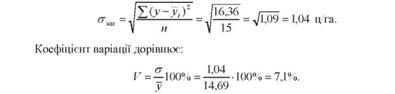
Отже, коливання фактичної урожайності навколо прямої лінії в середньому становить 1,04 ц/га, або 7,1%. Невеликий коефіцієнт варіації вказує на те що рівняння прямої лінії досить точно відображає тенденцію зміни урожайності в часі.

Водночас аналіз динамічного ряду урожайності свідчить про те, що не зважаючи на значне коливання урожайності по роках, чітко простежується тенденція її підвищення і прискорення приростів в останні роки. Тому логічно припустити, що досліджуваний ряд динаміки можна вирівнювати за рівнянням параболи другого порядку.

Вирівнювання рядів динаміки за параболою другого порядку здійснюється в тих випадках, коли зміна рівнів ряду відбувається приблизно рівномірним прискоренням або уповільненням ланцюгових абсолютних приростів.

Рівняння параболи другого порядку характеризується трьома параметрами:

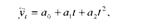
де а2 - показник щорічного прискорення (або уповільнення, якщо а2 зі знаком мінус) абсолютного приросту рівнів ряду.

Параметри параболи другого порядку аІ і а2 знаходять з такої системи нормальних рівнянь:

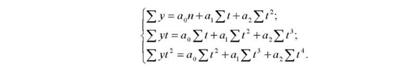
При 2г = 0 і 2 г3 = 0 система рівнянь значно спрощується, набуваючи такого вигляду:

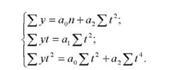
З цієї системи а1 визначають елементарно з другого рівняння

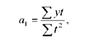
а а0 і а1 з системи двох рівнянь з двома невідомими:

Таблиця 10.11. Розрахунок даних для вирівнювання динамічного ряду урожайності соняшнику за параболою другого порядку способом найменших квадратів

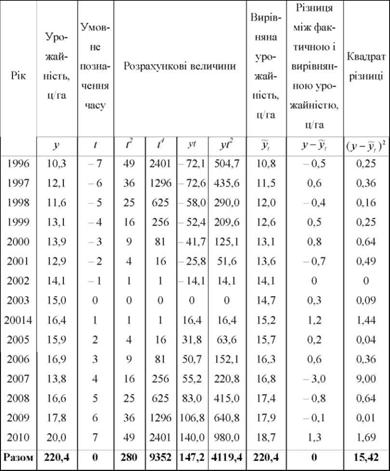
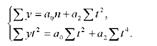
Використовуючи дані попереднього прикладу про динаміку урожайності соняшнику за 1996 - 2010 рр. (табл. 10.10), проведемо вирівнювання ряду за рівнянням параболи другого порядку способом найменших квадратів (табл. 10.11). Для спрощення розрахунків візьмемо і і = 0 і 2 і^ = 0.

Щоб визначити параметри а0, а1 і а2, рівняння параболи другого порядку, розв'яжемо таку систему рівнянь:

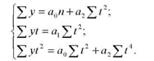
Підставимо знайдені величини в систему рівнянь:

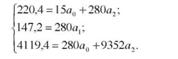
З другого рівняння визначимо значення а1:

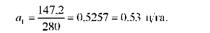
Розв'язавши перше і третє рівняння, матимемо значення параметрів

а0 і а2:

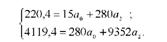
Для вирівнювання коефіцієнтів при а0 розділимо перше рівняння на 15, а друге - на 280. Дістанемо:

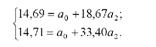
Віднявши з другого рівняння перше, отримаємо:

0,02 = 14,73 а2

Звідси

= і0,02 = 0,0014 ц/га. 2 14,73

Визначимо значення параметру а0, підставивши значення а2 в перше рівняння:

220,4 = 15 а2 + 280-0,0014;

220,4 - 0,39 220,01 л л ґп .

а0 =-=-= 14,67 ц/га.

0 15 15

Розв'язання системи рівнянь дає таке значення шуканих параметрів рівняння ( в ц/га ):

а0= 14,67; а1= 0,53; а2= 0,0014. Параметри рівняння параболи другого порядку можна визначити не тільки способом підстановки, а й безпосередньо користуючись формулами, що спрощують розрахунки:

Перевіримо правильність розрахунку параметрів, підставляючи в нормальне рівняння їхні числові значення:

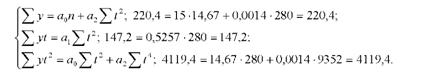
Отже, параболічний тренд має такий вигляд:

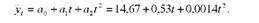
Пояснимо значення знайдених коефіцієнтів: а0= 14,67 ц/га - це початок відліку або вирівняне значення урожайності для центрального в ряду динаміки року, взятого за початок умовного відліку (2003 р., коли і = 0); а1 = 0,53 ц/га - середній щорічний приріст урожайності: а2= 0,0014 ц/га - середнє щорічне прискорення приросту урожайності.

Обчислимо за рівнянням параболи згладжене значення урожайності, підставляючи до рівняння замість і його числові значення ( від - 7 до +7; гр. 8 табл. 10.11):

в 1996р. при і = -7; ~ = 14,67 + 0,53(-7) + 0,0014(-7)2= 10,8 ц/га;

в 1997р. при і = -6; ~ = 14,67 + 0,53(-6) + 0,0014(-6)2= 11,5 ц/га і т. д.

Перевіримо правильність розрахунків:

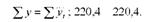
Як видно з розрахунків, вирівняні рівні урожайності дуже близькі до фактичних рівнів. Отже, парабола другого порядку досить точно відображує тенденцію зміни урожайності на досліджуваному відрізку часу.

Щ