У статистичному аналізі для всебічної характеристики розвитку складних соціально-економічних явищ і визначення ролі факторів у формуванні результативних показників використовуються різні форми і види індексів, що викликає необхідність відповідної їх класифікації. Економічні індекси класифікуються за такими ознаками: ступенем охоплення елементів сукупності, формою побудови, базою порівняння, характером ваг, складом явищ і змістом індексованих величин.
За ступенем охоплення сукупності індекси поділяють на індивідуальні, групові і загальні.
Індивідуальними називають індекси, що характеризують зміну окремих елементів складного соціально-економічного явища. їх прикладом можуть бути зміна обсягу виробництва окремих видів продукції (зерна, молока, м'яса і т. д.), цін, собівартості виробництва окремих видів продукції тощо. Якщо індекси охоплюють не всі елементи складного явища, а лише частину, то їх називають груповими або субіндексами. Наприклад, якщо визначаються зміни фізичного обсягу продукції або цін по рослинництву або тваринництву. Загальні або тотальні індекси характеризують зведені (узагальнюючі) результати спільної зміни всіх одиниць досліджуваної сукупності. Ці індекси охоплюють всі явища, наприклад підприємство, сільське господарство, економіку країни.
Залежно від форми побудови розрізняють агрегатні і середні індекси. Останні поділяють на середні арифметичні і середні гармонічні. Середні індекси - похідні, їх дістають в результаті перетворення агрегатних індексів. Перетворення агрегатного індексу в середній з індивідуальних полягає в підстановці або в чисельник, або в знаменник замість індексованого показника його вираз через відповідний індивідуальний індекс. Якщо така заміна виконана в чисельнику, то агрегатний індекс перетворюється в середній арифметичний, якщо ж в знаменнику - то в середній гармонічний з індивідуальних індексів. Як правило, середній арифметичний індекс застосовується при індексуванні об'ємних показників, а середній гармонічний - при індексуванні якісних показників.
Способи побудови індексів залежать від змісту і методології розрахунку досліджуваних статистичних показників, наявної вихідної інформації, цілей і завдань дослідження.
Індекси, подібні розглянутим вище, називають агрегатними, оскільки і чисельник і знаменник являють собою агрегати, з'єднання різнорідних елементів. Свою назву вони дістали від латинського слова "а%&-г%а", що означає "приєдную". Агрегатна форма індексів є основною формою індексів. Вона дістала найбільш широке застосування в статистичній практиці. В агрегатних індексах чисельник і знаменник подані підсумком добутків двох показників, один з яких змінюється, тобто виступає в ролі індексованої величини, а другий залишається незмінним і виступає в ролі сумірника.
За допомогою агрегатних індексів можна обчислити не тільки відносну зміну явища, але й абсолютні розміри цієї зміни. Різниця між чисельником і знаменником індексу характеризує абсолютну зміну складного явища за рахунок індексованої величини.
До розрахунку середнього арифметичного індексу удаються в тих випадках, коли за вихідними даними відомі індивідуальні індекси фізичного обсягу продукції (і4 = я1 : я0) і вартість продукції кожного виду за базисний період (я0Р0 ). Тоді загальний індекс фізичного обсягу можна обчислити як середню зважену із індивідуальних індексів. Для цього замінимо невідому кількість продукції звітного періоду ( я1) добутком і440 .
Ця можливість випливає з формули індивідуального індексу фізичного обсягу продукції. Тоді чисельник агрегатної форми індексу фізичного обсягу продукції одержить вираз £ я1 Р0 =^ і4я0Р0, а сам індекс фізичного обсягу прийме вигляд:

Одержана формула являє собою середню арифметичну із індивідуальних індексів фізичного обсягу продукції, зважену вартістю продукції базисного періоду.
Наведемо приклад обчислення середнього арифметичного індексу за такими даними (табл. 11.2).
Таблиця 11.2. Дані для розрахунку середнього арифметичного індексу фізичного обсягу продукції
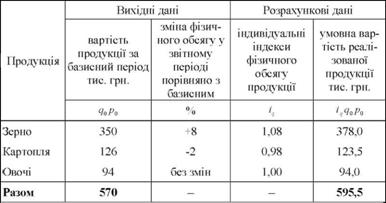
Оскільки за вихідними даними відомі індивідуальні індекси фізичного обсягу продукції (ід) і вартість кожного виду продукції (я0р0) за базисний період, середню зміну фізичного обсягу по всіх видах продукції визначимо за формулою середнього арифметичного індексу фізичного обсягу продукції
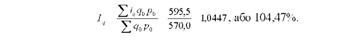
Отже, в середньому фізичний обсяг продукції у звітному періоді порівняно з базисним збільшився на 4,47%, або на 25,5 тис. грн. (і і,* р0 -190 р0 = 595,5 - 570,0).
Середній гармонічний індекс являє собою середню гармонічну із індивідуальних індексів і розраховується в тих випадках, коли відомі індивідуальні індекси цін (ір) і вартість кожного виду продукції за звітний період (,1 р1), але невідомі дані щодо ціни за одиницю продукції за базисний період (р0). Для отримання середнього гармонічного індексу цін
в знаменнику агрегатного індексу цін 1 = ^91 р1 ціну базисного періоду (р0) замінимо рівним їй відношенням р0 = -. В результаті знаменник агрегатної форми "су цін одержить вираз £91 р° =2-^д,^ а сам індекс цін буде мати такий вигляд:
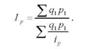
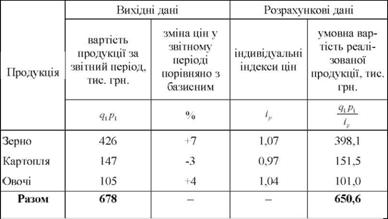
Порядок обчислення середнього гармонічного індексу покажемо на прикладі даних табл. 11.3.
Оскільки за вихідними даними відомі індивідуальні індекси цін (ір) і вартість кожного виду продукції за звітний період (д1 р1), середню зміну цін по всіх видах продукції визначимо за формулою середнього гармонічного індексу цін

Отже, в середньому ціни реалізації продукції у звітному році порівняно з базисним збільшились на 4,21%, а абсолютний приріст вартісного обсягу продукції внаслідок зростання цін становить 27,4 тис. грн.
(2 ,1 р1 -Ц - = =678,0 - 650,6).
ір
Таблиця 11.3. Дані для розрахунку середнього арифметичного індексу фізичного обсягу продукції
Залежно від бази порівняння індекси поділяють на: динамічні - характеризують відносну зміну складних соціально-економічних явищ у часі; планові - використовуються для визначення відносної величини планового завдання і узагальнюючої характеристики ступеня виконання плану; територіальні - виражають співвідношення складних масових явищ у просторі (між підприємствами, районами, областями, республіками, країнами і т.п.).
Більш докладно розглянемо динамічні індекси, оскільки вони найчастіше застосовуються в індексному аналізі.
При вивченні розвитку соціально-економічних явищ у динаміці виникає потреба порівнювати дані не за два, а за три періоди. У таких випадках необхідно вибрати базу порівняння. Залежно від бази порівняння розрізняють індекси з постійною (базисні) і змінною базою порівняння (ланцюгові).
В базисних індексах всі періоди порівнюються з одним, взятим за базу, а в ланцюгових - кожен наступний період порівнюється з безпосередньо йому попереднім.
Базисні і ланцюгові індекси можуть бути індивідуальними і загальними.
Індивідуальні базисні і ланцюгові індекси являють собою різновидність базисних і ланцюгових відносних величин динаміки. Тому способи обчислення тих и других показників тотожні.
Обчислення ж загальних базисних і ланцюгових індексів має свої особливості.
За характером ваг базисні і ланцюгові індексі класифікують на індекси з постійними і змінними вагами. При обчисленні індексів з постійними вагами за ваги для всього ряду приймаються сумірники будь-якого одного періоду. При обчисленні індексів із змінними вагами за ваги кожен раз беруть сумірники іншого періоду.
Наведемо приклади базисних і ланцюгових індексів з постійними і змінними вагами і покажемо їх взаємозв'язок. Для прикладу використаємо індекс фізичного обсягу продукції.
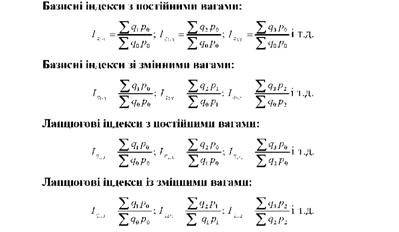
Між ланцюговими і базисними індексами існує такий взаємозв'язок: для індексів з постійними вагами добуток ланцюгових індексів дорівнює базисному індексу крайніх періодів. Наприклад, для індексів фізичного обсягу продукції:

Частка від ділення наступного базисного індексу з постійними вагами на попередній дорівнює відповідному ланцюговому індексу:
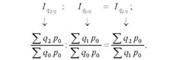
Обчислення базисних і ланцюгових індексів розглянемо на такому прикладі (табл. 11.4).
Визначимо базисні індекси фізичного обсягу реалізованої продукції з постійними вагами (в цінах 2008 р.):
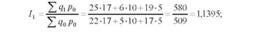
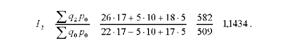
Ланцюгові індекси фізичного обсягу з постійними вагами:
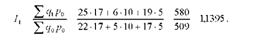
Перший ланцюговий і перший базисний індекси з постійними вагами завжди дорівнюють один одному
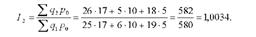
Обчислимо базисні і ланцюгові індекси цін із змінними вагами. За змінні ваги в цих індексах візьмемо обсяг реалізованої продукції у звітному періоді.
Базисні індекси із змінними вагами:

Ланцюгові індекси із змінами вагами:
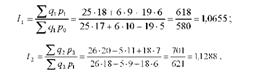
За складом явища розрізняють індекси постійного і змінного складу. Індекси, в яких змінюється одна величина, називають індексами постшного_складу (індекси фізичного обсягу продукції, цін, собівартості, продуктивності праці та ін.), а дві і більше величин - змінного складу (індекси вартісного обсягу продукції, валового збору, загальних витрат та ін.).
Відношення індексу змінного складу до індексу постійного складу дає індекс структурних зрушень.
Індекси змінного складу можна подати у вигляді добутку двох і більше взаємопов'язаних індексів постійного складу. Таке розкладання можна використовувати для аналізу зміни складного явища під впливом певних факторів. Так, наприклад, індекс вартісного обсягу продукції можна подати як добуток індексів фізичного обсягу продукції і цін:
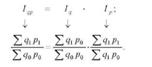
Індекс валового збору можна подати як добуток двох взаємопов'язаних індексів: урожайності і розміру і структури посівних площ:
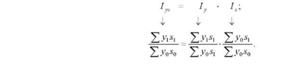
За змістом індексованих величин розрізняють індекси об'ємних і якісних показників. Індекси об'ємних показників характеризують зміну обсягу явища, числа одиниць сукупності. До цієї групи індексів відносять індекси фізичного обсягу продукції, розміру і структури посівних площ та ін. Індекси якісних показників відображають зміну ознак, властивостей одиниць сукупності. До індексів якісних показників відносять індекси цін, собівартості продукції, продуктивності праці, урожайності, продуктивності тварин та ін.
Індекси об'ємних показників (базисні і ланцюгові), як правило, будуються з постійними вагами. Так, при визначенні індексів фізичного обсягу продукції для всіх періодів використовують порівнянні ціни одного з попередніх періодів.
Індекси якісних показників (базисні і ланцюгові) обчислюються переважно із змінними вагами, так як в цих індексах застосовуються ваги поточних періодів, а поточний період від індексу до індексу змінюється. Щоб запобігти впливу на величину індексу відмінностей в структурі об'ємного показника, який відіграє роль ваги (наприклад, в структурі посівних площ, стада, затрат праці и т.д.), застосовують індекси, обчислені за тією самою стандартною структурою. У цьому разі ланцюгові і базисні індекси якісних показників визначаються з постійними вагами.
При побудові індексів важливе значення має вибір сумірників (ваг), оскільки індекси, обчислені з різними вагами дають різні економічні, а інколи й такі, що суперечать дійсності, результати. Тому при виборі ваг потрібно керуватися тим, що індекси мають бути актуальними і являти собою систему взаємозв'язаних показників.
У практиці статистики, як правило, при обчисленні індексів об'ємних показників беруть ваги базисного періоду, а при обчисленні індексів якісних показників - ваги звітного періоду. Крім того, для того, щоб добуток індексів об'ємного і якісного показників (наприклад, Ід і І ) був рівним індексу їх загальної взаємодії (Ір) необхідно, щоб один із індексів був побудований з вагами базисного періоду (І ), а другий - з вагами звітного періоду (Ір):
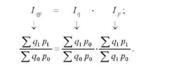
11.4. Територіальні індекси
11.5. Індексний аналіз
Розділ 12. Статистичні графіки
12.1. Роль і значення графічного методу
12.2. Основні елементи графіка. Правила побудови статистичних графіків
12.3. Види статистичних графіків і способи їх побудови
Список рекомендованої літератури